Математические методы классификации данных: общее представление о кластерном анализе

Еще одним методом, позволяющим упорядочить большой массив данных, является кластерный анализ. Этим термином на практике обозначают целый набор математических процедур, которые позволяют классифицировать имеющиеся у исследователя материалы. Выделяемые в ходе применения таких процедур группы объектов или переменных называют кластерами. Исходными данными в кластерном анализе выступают те же матрицы сходства и смешения, что и в многомерном шкалировании. По сути этот метод и является родственным методологии многомерного шкалирования, но отличается несколько большей простотой.

К настоящему времени разработано достаточно большое число различных алгоритмов кластерного анализа. Они различаются не только своими математическими процедурами, но и общей методологией (И. Д. Мандель [12]).

Некоторые из этих алгоритмов предполагают выделение групп объектов, кластеров по набору заранее заданных свойств. Такой подход принято обозначать как эвристический. Он определяет процедуры прямой классификации. К эвристическим процедурам принято относить и более гибкий подход, предполагающий такие алгоритмы, которые обеспечивают выделение собственного, уникального, набора свойств для каждого кластера. Эти алгоритмы получили название процедур комбинированной прямой классификации.

Принципиально отличаются от первых двух групп эвристического похода процедуры кластерного анализа, которые получили название оптимизационного направления. Такое направление определяет проблему выделения кластеров как собственно математическую задачу.

Наконец, выделяют еще аппроксимационное направление. В этом случае алгоритм кластеризации данных нацелен на то, чтобы обеспечить наилучшее приближение данных к заданному заранее представлению о классификации.

В рамках обозначенных подходов, которые на практике оказываются еще в значительной степени пересекающимися, разработан целый ряд различных алгоритмов. Наиболее развитыми и востребованными в рамках психологических исследований оказываются иерархические алгоритмы кластерного анализа. Эти алгоритмы принято относить к алгоритмам прямой классификации. Результатом применения алгоритма иерархического кластерного анализа оказывается так называемая дендрограмма, представляющая собой дерево иерархической классификации. Один из примеров такой классификации представлен на рис. 10.2.

Рис. 10.2. Дендрограмма.

Иерархическая кластеризация представляет собой пошаговую процедуру. Сначала выделяются объекты и переменные, обладающие наибольшим сходством друг с другом. Как показано на рис. 10.2, это объекты 6 и 5, а также 1 и 2. Затем на каждом следующем шаге к выделенным кластерам добавляются другие объекты или переменные до тех пор, пока все объекты не будут объединены в один кластер. При этом объекты не обязательно присоединяются к ранее выделенным группам по одному. Как показано на рис. 10.2, на последнем шаге происходит объединение сразу двух кластеров, выделенных еще на первом шаге.

Практические примеры

Факторная структура семантического дифференциала

Оценка времени реакции в задачах семантического решения, пример которой был рассмотрен выше (см. параграф 9.5), представляет собой один из популярных методов исследования системы значений. Этот метод был разработан в 1960;е гг. и стал особенно популярным в 1970—1980;е гг. в контексте исследований семантической памяти. Другой метод исследования значений был разработан несколько раньше — в 1940—1950;е гг., а в советской психологии он получил широкое распространение опять же в 1970;е гг. в связи с развитием отрасли психологии мышления, получившей название экспериментальной психосемантики. Речь идет о методе семантического дифференциала, разработанном Ч. Осгудом и его коллегами [25]. Важную часть обработки данных, получаемых на основе применения этого метода, составляют процедуры факторного анализа.

Сам метод семантического дифференциала достаточно прост. Испытуемому предлагается оценить ряд объектов, которые могут представлять собой как вербальные, так и невербальные стимулы по некоторому набору шкал. Эти шкалы, как правило, представляют собой набор качественных прилагательных. Чаще всего используются пары антонимов, как, например, холодный — теплый, большой — маленький, твердый — мягкий. Разновидностью этой методики является методика личностного семантического дифференциала, когда в качестве шкал семантического дифференциала используются те или иные личностные характеристики, а в качестве объекта — конкретные люди, наличие соответствующих личностных свойств у которых должны оценить эксперты в ходе наблюдения или беседы.

Результатом такой работы становится уже знакомая нам матрица смешения. Применяя процедуры факторного анализа, Ч. Осгуд [25] показал, что все многообразие оценок испытуемых, как правило, может быть описано с помощью трех базовых факторов: оценки, силы и активности. Однако вследствие тех или иных обстоятельств факторная структура семантического дифференциала в данном конкретном случае может оказаться иной.

В качестве примера использования процедур факторного анализа в оценке структуры семантического дифференциала рассмотрим студенческую работу, выполненную в рамках занятий общего психологического практикума в Институте психологии им. Л. С. Выготского РГГУ.

Студентам предлагалось самостоятельно выбрать объекты оценивания. При этом набор шкал семантического дифференциала задавался преподавателем. Использовались рекомендации А. Г. Шмелева^[1], также представленные им на сайте лаборатории «Гуманитарные технологии»^[2]. Вот этот список:

• 1) холодный — теплый;
• 2) легкий — тяжелый;
• 3) медленный — быстрый;
• 4) безобразный — красивый;
• 5) мягкий — твердый;
• 6) тихий — шумный;
• 7) горький — сладкий;
• 8) малый — большой;
• 9) вялый — бодрый;
• 10) противный — приятный;
• 11) податливый — упругий;
• 12) тусклый — яркий.

В одной из работ в качестве объектов для оценивания были выбраны предметы домашней утвари: утюг, сковородка, расческа, линейка, кастрюля, блюдце, губка и нитка. Испытуемый должен был ранжировать эти восемь предметов по каждой из 12 заданных шкал семантического дифференциала. Результатом такой работы стала матрица смешения, представленная в табл. 10.4.

Таблица 10.4

Результаты ранжирования восьми предметов домашней утвари по 12 шкалам семантического дифференциала

Достаточно беглого взгляда на эти результаты, чтобы убедиться в том, что оценки по ряду шкал для разных объектов могут в значительной степени совпадать. Так, мы видим, что по шкалам 1, 2, 9 и 11 «утюг» получает ранг восемь, т. е. этот объект оказывается в конце списка ранжирования, тогда как ранги для объекта «нитка» выводят этот объект практически на самый верх по этим шкалам. Таким образом, можно предположить, что дисперсия данных для этих четырех шкал на самом деле определяется значительным весом для них одного и того же признака, скрытого от непосредственного наблюдения. Как мы знаем, такие признаки называются факторами.

Попробуем реконструировать факторную структуру семантического дифференциала для результатов, представленных в табл. 10.4. Понятно, что «вручную» это сделать крайне сложно. Поэтому снова воспользуемся статистическим пакетом IBM SPSS Statistics. Этот пакет в стандартной версии содержит модуль, обеспечивающий выполнение процедур главного фактора.

Как обычно, начинаем с определения переменных. Этот шаг ничем не отличается от тех действий, которые нами были описаны в параграфе 9.6, когда мы рассматривали, как в IBM SPSS Statistics определяются переменные для регрессионного анализа. Переходим на вкладку «Переменные» и вводим названия наших 12 шкал семантического дифференциала. Поскольку в статистическом пакете существуют ограничения на обозначения переменных, в частности, не допускается использование в имени пробела, то в поле «Имя» указываем краткие названия, а в поле «Метки» — их полные обозначения (рис. 10.3).

Рис. 10.3. Определение переменных для факторного анализа в IBM SPSS Statistics

Теперь возвращаемся на вкладку «Данные» и вводим результаты оценки наших объектов по всем переменным из табл. 10.4. Таким образом получаем матрицу смешения, содержание которой и будет подвергнуто факторному анализу (рис. 10.4).

Рис. 10.4. Данные для факторного анализа.

Теперь в главном меню выбираем пункт «Анализ», далее «Снижение размерности» и «Факторный анализ…». Появляется окно настройки факторного анализа (рис. 10.5).

Рис. 10.5. Окно настройки факторного анализа в IBM SPSS Statistics

В левой части этого окна находится список переменных, которые можно выбрать. Справа от этого поля мы видим поле «Переменные», куда необходимо перенести те переменные, которые будут использоваться для факторного анализа. Перенесем сюда все наши переменные. Ниже этого поля расположено поле переменной, значения которой могут использоваться для отбора наблюдений. Поскольку мы хотим все данные подвергнуть факторизации, оставим это поле свободным. Кроме того, обратим внимание на возможности дополнительной более тонкой настройки факторного анализа.

Так, кнопка «Описательные…» дает возможность вывести дополнительную статистику, в частности корреляционную матрицу.

Кнопка «Извлечение…» позволяет выбрать вариант процедуры главного фактора и тем самым определить модель наших данных. По умолчанию здесь установлена процедура главных компонент, которая, как мы помним, определяет базовую полную компонентную модель факторного анализа. Этот вариант используется наиболее часто и, если у вас нет особых оснований использовать другую процедуру, стоит оставить его. Также нажатие кнопки «Извлечение…» позволяет задать критерий извлечения факторов: на основе собственных значений (латентных корней) или на основе заранее заданного числа факторов. По умолчанию используется первый вариант, при котором будут отсекаться факторы, собственные значения, т. е. значения латентных корней, для которых оказываются меньше единицы. Этот критерий также можно переопределить.

Более важной представляется кнопка «Вращение…». Выбор этой кнопки дает возможность задать процедуру последующего вращения факторов. Выберем для примера процедуру варимакс. Это наиболее часто используемый в психологических исследованиях вариант вращения.

Закончив настройку факторного анализа, нажимаем «ОК». Появляется окно вывода, которое может содержать различный набор результатов в зависимости от того, какие настройки мы выбрали. Наиболее важными являются результаты, представленные в таблицах «Полная объясненная дисперсия», «Матрица компонент» и аналогичная ей «Матрица повернутых компонент» .

Таблица «Полная объясненная дисперсия» важна для понимания того, сколько факторов было выделено в качестве важных и какой процент дисперсии они объясняют каждый в отдельности и все вместе. Рассмотрим ее более подробно (табл. 10.5).

В первом столбце таблицы перечислены выделенные компоненты, их 12 — по числу исследуемых переменных. Далее мы видим величины начальных собственных значений, иначе называемых латентными или характеристическими корнями. Столбец, содержащий такие данные, разделен па три части. В крайней левой части указаны сами значения латентных корней. Поскольку используется полная компонентная модель, сумма этих значений оказывается равной числу переменных, т. е. 12. Правее указаны проценты дисперсии, которые описываются каждой из этих компонент, выделенных в ходе факторного анализа, и рядом — накопленные значения этих процентов. Как видно, в ходе анализа главных компонент выделено три значимых фактора, значения латентных корней для которых оказываются больше единицы. Эти три фактора объясняют в целом около 86% дисперсии данных. Столбец «Суммы квадратов нагрузок извлечения» резюмирует этот результат.

Таблица 10.5

Значения латентных корней и объясненная дисперсия в результатах факторного анализа в IBM SPSS Statistics Полная объясненная дисперсия.

Метод выделения: Анализ главных компонент.

В последнем столбце отражены те же результаты после применения процедуры вращения варимакс. Как видно, произошло перераспределение значений латентных, или характеристических, корней. В результате веса второго и третьего факторов несколько увеличились, а первого — уменьшился. Обратим внимание также на тот факт, что если раньше первый фактор описывал более 62% общей дисперсии, второй — около 15%, а третий — менее 9%, то после вращения веса первого и второго факторов оказываются примерно равными, так что оба они описывают примерно по 35% общей дисперсии, а третий фактор — более 15,5% дисперсии данных.

Полученная в ходе применения процедур главных компонент факторная матрица для семи переменных по трем факторам, значения латентных корней для которых оказались выше единицы, представлена в табл. 10.6. Дело в том, что остальные переменные оказываются избыточными и не позволяют осуществить факторный анализ, и потому они были отброшены, так что на самом деле анализ главных компонент был осуществлен только для этих переменных. Это наглядно отражено в табл. 10.5: семь компонент описывают практически 100% общей дисперсии, вклад остальных компонент оказывается на уровне погрешности вычислительных возможностей компьютера.

Таблица 10.6

Матрица факторных нагрузок до вращения

Матрица компонент*

Метод выделения: Анализ главных компонент. * Извлеченных компонент: 3.

Обратим внимание на третий фактор в этой таблице факторных нагрузок. Как очевидно из табл. 10.6, все весовые коэффициенты для данного фактора оказываются чрезвычайно низкими. Относительно высокая нагрузка может быть отмечена только для переменной «вялый — бодрый». Однако эта переменная одновременно имеет еще более высокую нагрузку по первому фактору, что затрудняет его интерпретацию. Поэтому стоит обратиться к результатам, полученным после применения процедуры вращения варимакс. Эти данные представлены в табл. 10.7.

Таблица 10.7

Матрица факторных нагрузок после вращения

Матрица повернутых компонент''

Метод выделения: Анализ главных компонент.

Метод вращения: Варимакс с нормализацией Кайзера. ' Вращение сошлось за 6 итераций.

Как видно, первый фактор после вращения имеет самые высокие нагрузки по переменным «мягкий — твердый» (0,83), «тихий — шумный» (0,85) и «вялый — бодрый» (0,92). Иными словами, на одном полюсе этого фактора оказываются такие характеристики, как «мягкий», «тихий» и «вялый», а на другом — «твердый», «шумный» и «бодрый». По-видимому, это фактор активности, предполагаемый в стандартной процедуре семантического дифференциала. Второй фактор, как видно, задан оппозицией «малый» — «большой». Очевидно, это фактор размера. Наконец, третий, наименее значимый фактор имеет максимальные нагрузки по шкалам «легкий — тяжелый» (0,93) и «тусклый — яркий» (0,81). Таким образом, он задает оппозицию «легкий» и «тусклый», с одной стороны, и «тяжелый» и «яркий» — с другой. Принимая во внимание метафоричность процедуры оценивания предметов, но методу семантического дифференциала, можно сказать, что это фактор веса. Его можно также интерпретировать как фактор силы, который также предполагается базовыми предположениями теории Ч. Осгуда.

Таким образом, после применения процедуры вращения факторов мы получили три фактора, которые в порядке уменьшения их значимости можно интерпретировать как факторы активности, размера и веса (силы). Это лишь частично совпадает со стандартной факторной структурой семантического дифференциала, описанного Ч. Осгудом [25]. Такой факт можно объяснить особенностями объектов, которые были использованы для оценивания. Возможно, однако, что это связано и с особенностями процедуры выделения факторов.

Дело в том, что исторически раньше была предложена процедура факторного анализа, известная как центроидный метод. Его автором является Л. Тёрстоун (L. Thurstone [27]). Эта процедура относится к множественным групповым процедурам факторного анализа, которые являются расширением диагональной процедуры. Именно этот метод впервые и был использован Ч. Осгудом при построении семантического дифференциала.

Центроидный метод может дать интересные результаты в ситуации, когда у нас имеется большое число слабокоррелируемых переменных. И хотя в нашем случае мы имеем дело всего с 12 переменными, корреляции между ними, действительно, не слишком высоки.

К сожалению, статистический пакет IBM SPSS Statistics нс предоставляет нам возможности использования центроидного метода. В связи с этим обратимся к помощи статистического пакета STATISTICA.

Работа с этим пакетом несколько отличается от работы с пакетом IBM SPSS Statistics. После запуска программы необходимо создать файл данных или импортировать его из другой программы, например из файла, созданного MS Excel или IBM SPSS Statistics.

По умолчанию после запуска программы создается файл данных, содержащий десять переменных и десять наблюдений. Для нас это не совсем подходит. Удалим две строки наблюдений и добавим две переменные. Затем дважды щелкнем по имени первой переменной — по умолчанию она называется Var1. Таким образом, мы переходим в окно определения переменных (рис. 10.6).

Укажем название нашей первой переменной в поле Name. В поле Long пате обозначим полное имя пашей переменной — это поле аналогично полю «Метки» в IBM SPSS Statistics. Далее нажимаем кнопку «>>» для перехода к определению следующей переменной и так задаем названия всем нашим 12 переменным. После этого нажимаем «ОК» .

Теперь можно ввести результаты наших измерений по 12 шкалам семантического дифференциала (рис. 10.7).

Рис. 10.6. Окно определения переменных в STA TISTICA

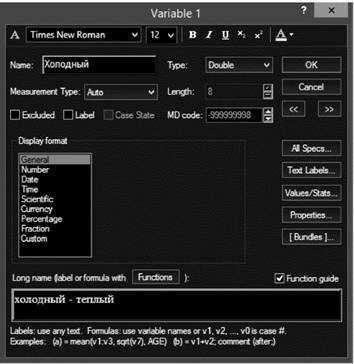
Рис. 10.7. Матрица смешения для 12 переменных и восьми объектов в STATISTICА

После того как все данные будут введены, переходим на вкладку Statistics и выбираем Mult/Exploratory и в открывшемся списке -.

Factor. Появляется первое окно настройки факторного анализа. На этом шаге нам необходимо указать переменные, для которых будет построена корреляционная матрица (рис. 10.8). Для выбора переменных достаточно нажать кнопку Variables (Переменные), а в появившемся окне — Select АН (Выбрать все). После этого закрываем окно выбора переменных, нажав «ОК» и возвращаемся к первому окну настройки факторного анализа. Указываем в соответствующем поле, что представляют собой наши данные — матрицу смешения Raw Data или корреляционную матрицу Correlation Matrix. В нашем случае выбираем матрицу смешения. Нажимаем «ОК» .

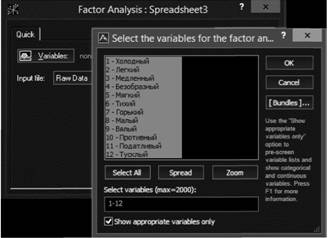
Puc. 10.8. Выбор переменных для факторного анализа в STATISTICА

Появляется второе окно настройки факторного анализа (рис. 10.9). Это основное окно, которое позволяет нам выбрать процедуру факторного анализа, определить критерий отбора факторов и вывести корреляционную матрицу.

Для того чтобы выбрать процедуру факторного анализа, отличную от заданного по умолчанию метода главных компонент, необходимо перейти на вкладку Advanced, как показано на рис. 10.9. Выбираем Centroid method - центроидный метод. Устанавливаем число факторов, которое мы хотим выделить, и минимальные собственные значения. Рекомендуется увеличить значение максимального числа факторов, так как STATISTICА выводит результаты только для указанного в этом окне числа факторов. Кроме того, при выборе центроидного метода оказываются активными поля числа итераций для оценки общностей и минимального изменения общностей на очередном шаге итерации. Как правило, значения по умолчанию оказываются вполне приемлемыми и достаточными.

Рис. 10.9. Основное окно настройки факторного анализа в STATISTICА

После того как мы нажмем «ОК», может появиться окно предупреждения о том, что имеющиеся у нас данные не вполне подходят для факторного анализа и поэтому матрица корреляций была скорректирована. Именно это мы и будем наблюдать в случае анализа наших данных. Нажимаем «ОК» и попадаем в окно результатов (рис. 10.10).

Это окно содержит пять вкладок. Вкладка Quick обеспечивает вывод основных результатов анализа. Обычно возможностей, которые она предоставляет, оказывается вполне достаточно. Исследователю предоставляется возможность посмотреть собственные значения — Eigenvalues, т. е. значения латентных корней, матрицу и двумерные графики факторных нагрузок для выделенных факторов, а также задать процедуру вращения факторов.

Сначала посмотрим собственные значения, нажав соответствующую кнопку. Однако этого можно и не делать, так как сами значения латентных корней уже отражены в кратком резюме в верхней части окна результатов.

Рис. 10.10. Окно результатов факторного анализа в STAT1STICA

Видно, что выделены два фактора. Значение латентного корня для первого фактора примерно равно 6,98, для второго — 1,69. Если мы все-таки нажмем кнопку собственных значений, то увидим, что первый фактор описывает чуть больше 58% общей дисперсии, второй — немного больше 14%. В сумме эти два фактора объясняют 72,28% дисперсии. Как видим, все эти значения оказываются несколько меньше тех, что были отмечены нами в случае применения процедуры главных компонент как по числу факторов, так и по величинам собственных значений и объясняемой ими дисперсии.

Теперь можно посмотреть факторные нагрузки всех наших переменных до вращения (рис. 10.11) и после вращения, применив, как и в прошлый раз, процедуру варимакс (рис. 10.12).

Сначала рассмотрим результаты первоначальной факторизации. Девять переменных демонстрируют высокие нагрузки, но первому фактору и одна — по второму.

Поскольку первый фактор обеспечивает высокие нагрузки для довольно большого числа переменных, для его интерпретации выделим переменную, имеющую наибольший весовой коэффициент по этому фактору. Это переменные «противный — приятный» и «податливый — упругий», причем они имеют разные знаки, так что образуется оппозиция: «приятный» и «податливый» против «противного» и «упругого». Скорее всего, это фактор удовольствия (оценки).

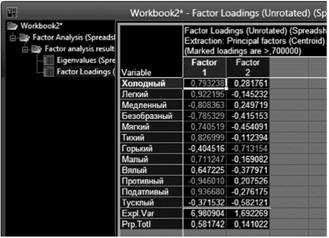
Puc. 10.11. Весовые коэффициенты для двух факторов, выделенных центроидным методом до вращения.

Puc. 10.12. Весовые коэффициенты для двух факторов, выделенных центроидным методом после вращения (метод варимакс).

Как очевидно, единственной переменной, имеющей высокую нагрузку по второму фактору, оказывается переменная «горький — сладкий». Получается, что это фактор вкуса. Однако следует помнить, что речь идет о предметах домашней утвари, которые мы обычно не пробуем на вкус. Поэтому обратимся к результатам оценки наших объектов, представленным в матрице смешения (см. табл. 10.4). Видно, что самыми «сладкими» оказались объекты «кастрюля» и «блюдце». Эти предметы имеют отношение к еде и, следовательно, к вкусовым ощущениям. Таким образом, наше предположение подтверждается.

В результате применения процедуры вращения варимакс значительного перераспределения весовых характеристик двух факторов фактически не происходит. Первый фактор по-прежнему оказывается доминирующим, описывая примерно 52% общей дисперсии. Второй фактор теперь описывает около 20% дисперсии. Неудивительно, что общая факторная структура практически не меняется. Первый фактор, как и ранее, описывается переменными «противный — приятный» и «податливый — упругий». Второй фактор снова дает максимальную нагрузку переменной «горький — сладкий». Однако к этой переменной добавляется еще переменная «безобразный — красивый». Это, по-видимому, несколько усложняет интерпретацию полученной факторной структуры. Поэтому стоит вернуться к первоначальному решению или попробовать использовать какую-либо другую процедуру вращения.

На рис. 10.13 представлена матрица факторных нагрузок после применения процедуры вращения эквамакс. Как мы помним, эта процедура соединяет в себе процедуры вращения квартимакс и варимакс. Мы видим, что паши выводы, касающиеся первоначальной факторной структуры, подтверждаются.

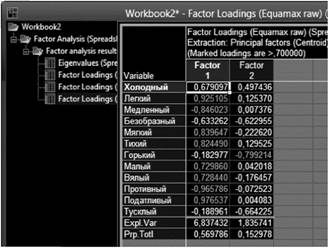
Рис. 10.13. Весовые коэффициенты для двух факторов, выделенных центроидным методом после вращения (метод эквамакс).

Подводя итог, следует обратить внимание на то, насколько различными оказались решения, полученные двумя разновидностями факторного анализа. Это свидетельствует о том, что эксплораторный вариант факторного анализа в первую очередь является всегонавсего удобным инструментом, позволяющим исследователю представить имеющиеся у него данные в более компактном виде, и вовсе не открывает ему новой реальности психической организации, как это иногда принято считать.

• [1] Шмелев А. Г. Семантический дифференциал в режиме онлайн как инструмент исследования семантико-перцептивных универсалий и личностно-смысловых установок / А. Шмелев // Психология субъективной семантики: истоки и развитие: сб. статей. М.: Смысл, 2012. С. 103−118.
• [2] URL: ht.ru/cms/component/content/article/101 709 (дата обращения 10.03.2014).