Отношения между понятиями

Формальная логика изучает и описывает имеющие большое значение для познавательной деятельности человека разнообразные отношения между понятиями, выясняет, как они проявляются в реальной практике процесса познания.

Если сравнивать различные понятия по их содержанию, то можно увидеть, что содержание одних понятий включает общие признаки, а содержание других понятий общих признаков не имеет. Например, понятия «повесть» и «рассказ» имеют общий существенный признак — «быть художественным произведением». Но если мы сравним понятия «повесть» и «автор повести», то увидим, что общих признаков у них нет, так как содержание пер;

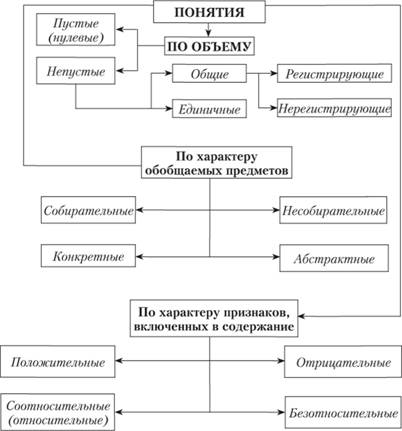
Рис. 3.4.

вого — «быть художественным произведением», а содержание второго — «человек» и «написать повесть» .

Сравнимыми называются понятия, имеющие в своем содержании общие существенные признаки. Например: «любовь» и «дружба» .

Несравнимыми называются понятия, не имеющие в своем содержании каких-либо общих признаков. Например: «Закон Божий» и «ЭВМ» .

Если понятия имеют в своем содержании общее родовое понятие, то они сравнимы, если не имеют, то несравнимы.

В зависимости от объема сравнимые понятия делятся на две группы: совместимые и несовместимые.

Для иллюстрации отношений между объемами понятий применяются схемы, впервые введенные в научную практику немецким ученым Л. Эйлером (1707−1783), предложившим схематическое изображение объемов понятий с помощью геометрических фигур (кругов, прямоугольников, эллипсов).

Совместимые понятия

Совместимые понятия — это понятия, объемы которых полностью или частично совпадают.

Между совместимыми понятиями могут быть отношения 1) равнозначности (тождества); 2) пересечения (частичного совпадения) объемов; 3) подчинения (отношение рода и вида).

1. В отношении равнозначности (равнообьемности) находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают. Например: «основатель формальной логики» и «Аристотель». Эти понятия равны по своему объему (рис. 3.5).

Рис. 3.5:

А — основатель формальной логики; В — Аристотель (384−322 до н.э.).

2. В отношении пересечения (перекрещивания) находятся понятия, имеющие некоторые общие признаки, т. е. объем одного из них частично входит в объем другого (рис. 3.6).

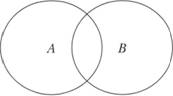
Рис. 3.6:

А — студент; В — спортсмен.

3. В отношении подчинения (субординации) находятся понятия, одно из которых полностью входит в объем другого, составляя его часть (рис. 3.7).

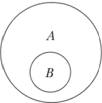
Рис. 3.7:

А — город; В — город Москва.

Понятие с большим объемом (А) называется подчиняющим, понятие с меньшим объемом (В) — подчиненным.

Если в отношении подчинения находятся общие понятия, то подчиняющее понятие называется родом, подчиненное — видом.

Отношение «род — вид» широко используется в логических операциях, производимых над понятиями, — обобщение, ограничение, определение, деление.

Несовместимые понятия

Несовместимые — это такие понятия, объемы которых не совпадают ни в одном элементе.

Между несовместимыми понятиями могут быть отношения:

• 1) соподчинения (координации); 2) противоречия (контрадикторности); 3) противоположности (контрарности).
• 1. Два или более понятий находятся в отношении соподчинения (координации) к третьему, если они не имеют общих элементов объема и это третье понятие является подчиняющим для каждого из них (рис. 3.8).

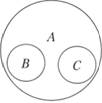
Рис. 3.8:

А — город; В — город Москва; С — город Брянск.

2. В отношении противоречия (контрадикторности) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки отрицает, не заменяя их другими признаками (рис. 3.9).

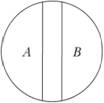
Рис. 3.9.

А — черный; не-А — нечерный.

3. В отношении противоположности (контрарности) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки отрицает, заменяя их исключающими признаками (рис. 3.10).

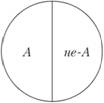
Рис. 3.10.

А — черный; В — белый Отношения между понятиями используются во всех разделах человеческого знания, где требуется предельно точно выразить смысл понятия, уточнить его отношение к другим сходным понятиям, при построении схем, диаграмм, а также в педагогическом процессе.