Квантовая теория поля и теория струн

Основная цель данной главы состоит в обеспечении понимания студентом концептуального устройства квантовой теории поля. В результате изучения материала данной главы студент должен:

знать

• • основные концепты квантовой теории поля;
• • основные проблемы квантовой теории поля;

уметь

• давать адекватную характеристику концептам частицы, поля, перенормировки, калибровочной инвариантности, спонтанного нарушения симметрии, асимптотической свободы;

владеть

• • концептуальным осмыслением актуальных проблем квантовой теории поля;
• • способами методологической оценки квантово-полевых новаций.

Ключевые слова: перенормировка, калибровочная инвариантность, спонтанное нарушение симметрии, асимптотическая свобода.

Концептуальное устройство квантовой теории поля. Алгебраическая квантовая теория поля

Квантовая механика позволила справиться с большим клубком проблем. Тем не менее уже в первые годы ее создания (речь идет о середине 1920;х гг.) стало понятно, что она должна иметь продолжение. Показательно, например, что квантовая механика, способствовавшая определению дискретного набора значений энергии электрона в атоме водорода, была недостаточна для рассмотрения излучения, сопровождавшего переход атома водорода из возбужденного состояния на более низкий уровень. Она актуальна лишь для физических систем с неизменным числом частиц.

Другая злободневная проблема состояла в необходимости прояснения концепта «поле». Было достаточно очевидно, что революционные по своему характеру концептуальные достижения квантовой механики не могут остаться бесследными для истолкования природы не только отдельных частиц, которые обозначали термином «вещество», но и для поля, в частности электромагнитного поля, фигурировавшего в электродинамике Максвелла — Лоренца — Эйнштейна.

Поиски концептуального каркаса, необходимого для понимания тех процессов, которые не могли быть осмыслены в рамках квантовой механики, привели к квантовой теории поля с ее первым историческим представителем, квантовой электродинамикой. Выдающийся вклад в развитие квантовой электродинамики внесли Поль Дирак и Паскуаль Йордан, авторы идеи квантования поля и операторов рождения и поглощения частиц^[1].

Авторы статей и книг, описывающие историю квантовой теории поля, обычно стараются показать, как, стартуя от квантовой механики, исследователи переходили к новой теории. Вроде бы квантовая теория поля является всего лишь обобщением своей исторической предшественницы, а именно квантовой механики. Необходимо, однако, учитывать, что квантовая теория поля обладает своим собственным революционным концептуальным содержанием. Оно не выводится из квантовой механики. Переходя непосредственно к концептуальному содержанию квантовой теории поля, обратим особое внимание на актуальность ее концептов. Каким же образом обычно конструируется концептуальный аппарат квантовой теории поля? По мнению автора, решающее значение имеют следующие предельно актуальные в концептуальном отношении шаги.

Во-первых, используется принцип наименьшего действия и, следовательно, функция Лагранжа. Этот шаг, конечно же, крайне существенен. В частности, он задает некоторую динамическую перспективу. Динамика не только не отодвигается в тень, но даже выдвигается на передний план.

Во-вторых, учитывается объемная распространенность физической системы. В результате в интеграл, необходимый для подсчета действия (S), вводится элемент объема (dv):

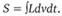(6.1)

В-третьих, посредством лагранжиана выражаются все сопряженные величины, в частности обобщенные импульс и координата.

В-четвертых, всем физическим величинам, в том числе скалярным и векторным потенциалам, сопоставляют операторы.

В-пятых, вводятся операторы рождения и уничтожения частиц.

В-шестых, вводится концепт операторно-значимого поля (функции)^[2].

В-седьмых, конструируются перестановочные отношения для сопряженных величин, выражаемые посредством коммутирующих и некоммутирующих операторов. При этом центральное значение придается перестановочным соотношениям операторов рождения и уничтожения частиц.

Подчеркивая принципиальное отличие квантовой теории поля от квантовой механики, следует, прежде всего, рассмотреть различие волновой функции и операторно-значимой функции. Волновая функция является амплитудой вероятности, а не оператором. Она находится под воздействием операторов, что приводит к выделению значений наблюдаемых величин. Операторно-значимая функция имеет изначальную операторную природу. Лишь после некоторых манипуляций с нею она превращается в оператор, действующий в гильбертовом пространстве волновых функций. Речь идет о свертке. Свертка — это математическая операция двух функций/и g, порождающая третью функцию, которая обычно может рассматриваться как модифицированная версия одного из первоначальных уравнений. В рассматриваемом случае это означает, что оператор, действующий в гильбертовом пространстве состояний, является модифицированной формой операторно-значимой функции.

Таким образом, в квантовой механике основным концептом является понятие волновой функции. В квантовой же теории поля основным концептом является не волновая функция, а операторно-значимая функция. Исторически ситуация сложилась таким образом, что эту функцию стали называть полем, что приводит к многочисленным издержкам. Дело в том, что не проводится четкое различение поля как некоторого физического объектного образования и поля как математического концепта, обычно понимаемого как совокупность некоторых математических понятий. В физике говорят, в частности, об электромагнитном и гравитационном поле, но также об электронном и позитронном поле, поле скоростей и импульсов. Употребление термина «поле» в самых различных контекстах способно привести к путанице. Стараясь избежать ее, автор еще раз обращает внимание на особую значимость в квантовой теории поля концепта операторно-значимой функции. Он имеет в теории основополагающее значение. Термин «квантовая теория поля» вряд ли заслуживает одобрения в силу многозначности термина «поле» .

Подводя итоги сопоставления квантовой механики и квантовой теории поля, отметим, что на их преемственность указывает операторная идеология. В обеих теориях физическим наблюдаемым системам соответствуют операторы. Но состояния физических систем в концептуальном отношении описываются в двух рассматриваемых теориях по-разному. Пытаясь понять историю развития физических теорий, всегда следует иметь в виду, что развитая теория является ключом для понимания ее предшественниц. Такого рода интерпретация никогда не реабилитирует устаревшие концепты полностью. Подобно тому, как квантовая механика не реабилитирует классическое понимание физических наблюдаемых величин, квантовая теория поля не реабилитирует понятие волновой функции.

Физические явления столь многообразны, что для их понимания необходим достаточно универсальный математический язык. В противном случае, обратившись к избранной концептуальной системе, например, к представлению в гильбертовом пространстве, можно упустить из вида нечто очень важное, адекватно описываемое другими представлениями. Поиски в указанном направлении привели к алгебре, прежде всего к так называемой с*-алгебре. Разумеется, ей приписывается физическая значимость^[3].

Как известно, в квантовой теории поля большое значение придается соответствию между операторами и наблюдаемыми. Выяснилось, что оно может быть обобщено, для этого достаточно считать, что наблюдаемые в качестве элементов совокупности должны реализовать алгебраические операции сложения и умножения. Таким образом, основанием квантовой теории поля являются наблюдаемые и соответствующие алгебраические системы. Наблюдаемые совсем не обязательно соотносить с точками пространства Минковского, как это делается в обычной формулировке квантовой теории поля. При алгебраическом подходе измерения соотносят с некоторой областью пространства Минковского. Физически актуальная информация содержится не в наблюдаемых (О) и не в алгебрах (А), а в переходе O>А (О).

Каждая алгебра, А (О) относится к определенной области пространства Минковского и в этом смысле является локальной. Но необходимо учесть также связь между различными областями. Пытаясь выразить ее, не ограничиваются одной локальной алгеброй, а обращаются к сети алгебр. Условие выполнения принципа причинности состоит в требовании коммуникации наблюдаемых одной области с наблюдаемыми другой области. А это означает, что концептуальным основанием квантовой теории поля является сеть алгебр.

Следует отметить, что алгебраический подход в квантовой теории поля стал самой успешной попыткой изложить эту теорию в аксиоматическом виде. Решающее значение придается трем аксиомам, а именно релятивистской инвариантности, причинности и спектральности (энергии всех допустимых состояний квантовой системы должны быть положительными). Эти три аксиомы налагаются на соотношение О > А (О).

Но удержаться в рамках чисто аксиоматического подхода даже в алгебраической квантовой теории поля не удается. В той или иной форме необходимо учесть специфику физических явлений. Это делается посредством правил суперотбора, накладывающих ограничения на величины наблюдаемых физических величин.

Выводы

• 1. Квантовая теория поля не реабилитирует понятие волновой функции.
• 2. Концепт операторно-значимой функции не имеет аналога в квантовой механике.
• 3. Алгебраическая квантовая теория поля позволяет по-новому оценить все те концептуальные узлы, с которыми имеет дело обычная квантовая теория поля^[4]. Это обстоятельство привлекло внимание философов лишь в 1980;х гг.

• [1] Обычно возраст квантовой электродинамики отсчитывается от работы П. Дирака: Dirac Р. А. М. The quantum theory of emission and absorption of radiation // Proceedings of the Royal Society of London. Ser. A. 1927. Vol. 114. No. 767. P. 243−256.
• [2] Операторно-значимая функция А является функцией, значения которой A (t) являются операторами, зависящими от переменной t. Она может быть реальной или комплексной величиной, вектором из области топологического пространства, элементом некоторого множества.
• [3] Об алгебраической квантовой теории поля см.: Хоружий С. С. Введение в алгебраическую квантовую теорию поля. М.: Наука, 1986; Боголюбов Η. Н., Логунов А. А., Оксак А. И., Тодоров И. Т. Общие принципы квантовой теории поля. М.: Наука, 1987; Haag R. Local quantum physics: fields, particles, algebras. Berlin: Springer, 1992.
• [4] Термин «квантовая теория поля» закрепляется за теорией, основным концептом которой является операторно-значимая функция. От нее будем отличать алгебраическую квантовую теорию поля, руководствующуюся концептом «алгебра наблюдаемых». (Прим. авт.)