Анализ рядов динамики

В данной главе рассматриваются правила построения и анализа рядов динамики. Теоретическое изложение материала сопровождается примерами, которые позволяют познакомиться с расчетом аналитических показателей динамики.

Понятие о рядах динамики

Ряд динамики (динамический ряд, временной ряд) представляет собой ряд расположенных в хронологической последовательности статистических величин, которые отражают развитие изучаемых явлений. Каждый ряд динамики имеет два основных элемента:

• • время (t);
• • уровень ряда (yi), т. е. конкретные значения показателя.

Уровни динамического ряда могут быть выражены абсолютными, средними и относительными величинами. Примером такого представления уровней ряда динамики являются данные об изменении отдельных социально-экономических показателей по Российской Федерации (табл. 8.1).

Данные, приведенные в таблице, могут быть использованы для иллюстрации рядов динамики разного типа. Различают следующие виды рядов динамики:

• — моментные и интервальные;
• — ряды с равнои неравноотстоящими во времени уровнями;
• — стационарные и нестационарные.

Моментным является ряд динамики, уровни которого характеризуют изучаемое явление в конкретный момент времени (см. табл. 8.1, стр. 1). Такие ряды используют для описания величин типа запаса (остатки средств на счетах клиентов, объем собственных средств (капитала), объем основных фондов и т. д.).

Таблица 8.1

Изменение групп населения РФ по отношению к трудоспособному возрасту и занятости в экономике, 2007−2011 гг.

Источник•. Российский статистический ежегодник. 2012: стат. сб. / Росстат. М., 2012. С. 34.

Интервальным является ряд динамики, уровни которого характеризуют накопленный результат изменения явлений за определенные промежутки (интервалы, периоды) времени (см. табл. 8.1, стр. 2). Таким образом, интервальные ряды динамики используют для описания величин типа экономического потока, операции (проценты полученные, проценты уплаченные, комиссионные доходы и расходы, выпуск продукции, текущие затраты и т. п.).

Уровни интервальных рядов динамики обладают свойством суммарности, показатели моментных рядов такого свойства не имеют. Можно сложить показатели объема промышленной продукции за кварталы и получить итог производства за год. Но если за год сложить данные о числе рабочих на начало каждого квартала, полученная сумма не будет иметь реального смысла.

В рядах с равностоящими уровнями даты регистрации или окончания периодов представлены через равные, следующие друг за другом отрезки времени (см. табл. 8.1). В рядах с неравностоящими уровнями принцип равенства отрезков времени не соблюдается.

Ряд динамики, в изменении уровней которого не наблюдается общей направленности (тенденции), является стационарным. Напротив, нестационарный ряд отличается наличием общей направленности в изменении уровней изучаемого показателя. Так, уровни рядов динамики, которые представлены в табл. 8.1, имеют за 2007−2011 гг. разнонаправленные тенденции изменения: численность населения в возрасте моложе трудоспособного и старше трудоспособного растет, напротив, в трудоспособном возрасте — снижается; среднегодовая численность занятых в экономике изменяется неравномерно: с 2007 по 2008 г. — рост, с 2008 по 2010 г. — снижение; в 2011 по сравнению с 2010 г. — подъем.

При построении и анализе динамических рядов необходимо учитывать требование сопоставимости данных как в рамках одного ряда, так и в разных динамических рядах, если их исследуют совместно. Сопоставимость уровней динамического ряда рассматривают в нескольких аспектах:

• — по кругу охватываемых объектов;
• — по территории;
• — по методологии расчета показателей.

Несопоставимость по кругу охватываемых объектов возникает, например, в силу особенности учета изучаемых единиц совокупности, в результате изменений в классификации единиц и т. п. Так, в статистическом сборнике «Социально-экономическое положение Санкт-Петербурга и Ленинградской области» данные об объеме промышленной продукции представляют в двух вариантах: только по крупным и средним предприятиям; по полному кругу предприятий, включая малые предприятия и промышленные подразделения при непромышленных предприятиях. В связи с этим, используя для построения динамических рядов в качестве источника информации соответствующие показатели объема промышленной продукции, необходимо учитывать круг предприятий, по которому представлена информация.

Несопоставимость статистических данных по территории возникает в результате административно-территориальных изменений. Например, на основе Общероссийского классификатора экономических регионов публикацию статистических данных осуществляли в разрезе экономических районов: Северный, Северо-Западный, Центральный, Волго-Вятский, Центрально-черноземный, Поволжский, Северо-Кавказский, Уральский, Западно-Сибирский, Восточно-Сибирский, Дальневосточный, Калининградская обл.

В соответствии с Указом Президента РФ от 13 мая 2000 г. № 849 «О полномочном представителе Президента Российской Федерации в федеральном округе» на территории России были образованы семь федеральных округов: Центральный, Северо-Западный, Южный, Северо-Кавказский, Приволжский, Уральский, Сибирский, Дальневосточный. Их границы не совпадают с сеткой экономического районирования страны. В таком случае для обеспечения сопоставимости показателей динамики проводят прямой пересчет данных по первичному материалу.

И наконец, к несопоставимости уровней динамического ряда приводят различия в методике их расчета. В этом случае обычно делают пересчет предшествующих данных в соответствии с новой методикой.

Вопрос о сопоставимости встает и при анализе уровней разных динамических рядов. Так, для совместного анализа уровней моментной) и интервального рядов динамики моментные динамические ряды должны быть преобразованы таким образом, чтобы пересчитанные уровни охватывали те же промежутки времени, что и уровни интервального динамического ряда. Трудности сравнения взаимосвязанных рядов динамики возникают из-за наличия так называемого временного лага, который является мерой отставания во времени изменений одних явлений по сравнению с другими. Например, для расчета доли закончивших обучение студентов показатели года выпуска студентов следует сравнивать с показателями года приема этих же студентов, т. е. смещая данные с учетом срока обучения. При подготовке информации для анализа динамики необходимо учитывать сопоставимость условий, которые определяют формирование уровней динамического ряда. Например, показатели банковской деятельности с момента начала экономических реформ отражают несколько этапов развития: 1988−1992 гг. — период акционирования и разукрупнения государственных специализированных банков; 1992−1994 гг. — период количественного роста банков в условиях высокой инфляции; 1995−1998 гг. — период стабилизации числа банков; 1998−2001 гг. — период реструктуризации банков после финансового кризиса; с 2001—2008 гг. — период модернизации банковской системы, мировой финансовый кризис с середины 2008 г.

Разграничение в динамических рядах однородных этапов развития называют периодизацией динамики. Это, по существу, типологическая группировка во времени. Ряды динамики часто представляют в графическом виде, что значительно способствует проведению анализа развития явлений. Как правило, их динамику изображают в виде линейных (рис. 8.1) и столбиковых (рис. 8.2) диаграмм. Линейная диаграмма — ломаная линия — наиболее соответствует характеру моментных показателей, уровни которых в соответствии с их координатами наносят на график в виде точек. Интервальные же показатели теоретически правильнее изображать столбиками или ступенчатой линией. Однако на практике их динамику часто представляют в виде ломаной линии. Для построения графика используют прямоугольную систему координат; на оси абсцисс откладывают время, а на оси ординат — показатели ряда.

Для более наглядного отображения характера развития явлений рекомендуется наносить па график не сами уровни ряда, а их относительное изменение. На рис. 8.1 представлена сравнительная динамика трех показателей. Как следует из диаграммы, изменение в организациях числа замещенных рабочих мест работниками списочного состава и внешними совместителями происходит более равномерно по сравнению с динамикой числа замещенных рабочих мест работниками, выполнявшими работы по договорам гражданско-правового характера.

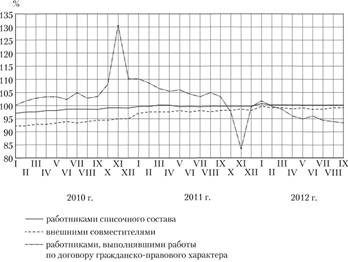
Рис. 8.1. Динамика числа замещенных рабочих мест в организациях (без субъектов малого предпринимательства), в % к соответствующему месяцу предыдущего года.

Приведенный пример свидетельствует также о том, что на одном графике целесообразно изображать несколько динамических рядов с целью их сравнения.

Существуют различные варианты графического изображения нескольких рядов динамики с помощью столбиковых диаграмм (рис. 8.2 и 8.3). Так, на рис. 8.2 приведена диаграмма изменения цен производителей промышленных товаров, при этом в виде линейной диаграммы выделены цены отдельных видов деятельности.

В 2011—2012 гг. динамика цен производителей промышленных товаров определятся, прежде всего, изменением цен в сфере добычи полезных ископаемых, а также в производстве и распределении электроэнергии газа и воды.

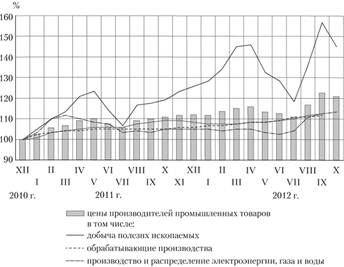
Рис. 8.2. Динамика цен производителей промышленных товаров, на конец месяца, в % к декабрю 2010 г.

На рис. 8.3 представлена столбиковая диаграмма, отражающая изменение в 2011—2012 гг. доли расчетов денежными средствами в общем объеме оплаченной продукции, выполненных работ, оказанных услуг за отрезки времени разной продолжительности: квартал, полугодие, девять месяцев.

При изучении динамики явлений для характеристики особенности их развития на отдельных этапах рассчитывают производные показатели: абсолютный прирост, коэффициент роста, темп роста и прироста, абсолютное значение 1% прироста. Расчет основан на сравнении уровней ряда динамики.

В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики — это результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу. Они характеризуют окончательный результат всех изменений в уровнях ряда за период от базисного до текущего уровня. Обычно за базу сравнения принимают начальный уровень динамического ряда. Цепные показатели динамики — это результат сравнения текущих уровней с непосредственно предшествующими. Они характеризуют интенсивность изменения уровней от срока к сроку.

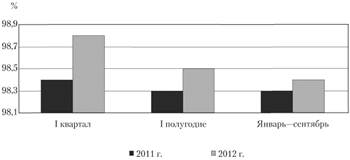
Рис. 8.3. Доля расчетов денежными средствами в общем объеме оплаченной продукции, выполненных работ, оказанных услуг.

Абсолютный прирост равен разности между текущим уровнем и уровнем более раннего периода. Интерпретацию абсолютного прироста осуществляют в тех же единицах, что и уровни ряда, с добавлением единицы времени, за которую определено изменение. Например, абсолютный прирост объема промышленной продукции составил 501 млрд руб. за квартал и 687 трлн руб. за год. Если текущий уровень уменьшился по сравнению с предыдущим периодом, то абсолютный прирост, имея отрицательное значение, характеризует абсолютную убыль (сокращение) уровня. Абсолютный прирост за единицу времени отражает абсолютную скорость изменения. Формулы абсолютного изменения уровня динамического ряда следующие:

• • цепного ;
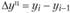• • базисного ,

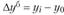где 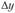- абсолютный прирост за t единиц времени; 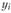- текущий (сравниваемый) уровень ряда; 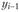- уровень ряда, непосредственно предшествующий текущему; 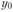- уровень ряда, который принят за базу сравнения.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных приростов равна соответствующему базисному приросту за весь период.

Так, в табл. 8.2 сумма показателей цепных абсолютных приростов (гр. 3) равна базисному абсолютному приросту за 2004- 2012 гг. (гр. 4).

Таблица 8.2

Изменение количества филиалов коммерческих банков региона, головные организации которых находятся в данном регионе (на начало года)

Для оценки эффективности изменения уровня динамического ряда используют относительные показатели динамики:

• — коэффициент роста, выраженный в долях единицы;
• — темп роста, выраженный в %.

Коэффициент роста Кр определяют по формулам:

• • цепной ;
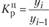• • базисный .

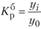Взаимосвязь цепных и базисных коэффициентов роста заключается в следующем:

• а) произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период. Так, в табл. 8.2 произведение цепных коэффициентов роста (гр. 5) равно базисному коэффициенту роста за 2004−2012 гг. (гр. 6: 0,8358 • 0,9821 •… • 0,48 = 0,1791);
• б) частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста. Например, в гр. 6 табл. 8.2, разделив базисный коэффициент роста за 2007 г. на базисный коэффициент роста за 2006 г., получим цепной коэффициент роста за 2007 г. (0,8209: 0,8209 = 1).

Для большей простоты и наглядности доказательства этой взаимосвязи используем данные за три периода:

• а) ;
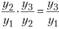• б) .

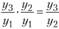Коэффициент роста показывает, во сколько раз увеличился уровень динамического ряда по сравнению с базисным, а в случае уменьшения — какую часть базисного составляет сравниваемый уровень. Темпы и коэффициенты роста отличаются только единицами измерения. Формулы расчета темпов роста следующие:

• • цепного ;
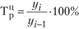• • базисного .

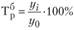Темпы прироста (сокращения) так же, как и темпы роста, исчисляют по годам (цепным методом) и накопленным итогом за длительный период (базисным методом). Формулы расчета темпов прироста следующие:

• цепного ;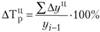

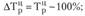
• базисного ;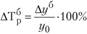

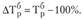
Темп прироста показывает, на сколько процентов изменилась величина уровня динамического ряда за изучаемый период времени. Если она сокращается, то темпы прироста будут иметь знак «минус» и характеризовать относительное уменьшение уровней ряда.

Для правильной интерпретации относительных показателей динамики явлений рекомендуется рассматривать их совместно с исходными уровнями ряда. Например, по данным Банка России, число филиалов действующих кредитных организаций на территории РФ в 2010 г. составило 92% уровня 2008 г., т. е. оно уменьшилось на 8%. А число филиалов действующих кредитных организаций за рубежом за этот же период увеличилось на 67%. Но при этом число филиалов на территории РФ на начало 2008 г. было 3455, а на начало 2010 г. стало 3183, в то же время на эти даты за рубежом их было всего 3, а стало 5.

Если уровень ряда принимает положительные и отрицательные значения (например, финансовый результат деятельности организации может быть прибылью или убытком), то темпы изменения и прироста не имеют экономической интерпретации и не рассчитываются.

Для цепных показателей прироста и его темпов рассчитывают показатель абсолютного значения одного процента прироста. Он равен отношению абсолютного прироста (цепного) к темпу прироста (цепному). Этот показатель может быть исчислен и иначе, т. е. как одна сотая часть предыдущего уровня:

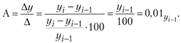
Аналитическое значение данного показателя состоит в том, что при возрастающей скорости (и растущем уровне) темпы роста могут иметь тенденцию к уменьшению или оставаться без изменения. В результате абсолютное значение одного процента прироста будет расти. Так, число предприятий и организаций в стране за 2007- 2008 гг. и 2010−2011 гг. увеличилось почти с одинаковым темпом прироста: соответственно 7,07 и 7,00%. При этом один процент относительного прироста в 2008 г. по сравнению с 2007 г. составляет 29,012 тыс. ед., а в 2011 г. по сравнению с 2010 г. — 35,938 тыс. ед. (табл. 8.3).

Таблица 8.3

Изменение числа предприятий и организаций в стране за 2007;2011 гг.

Таким образом, затухающий темп прироста вовсе не означает приостановки роста: при высоких абсолютных уровнях развития изучаемого явления может значительно увеличиться его абсолютный объем даже при небольшой величине темпов. Следовательно, чтобы правильно оценить значение показателя темпа, его нужно рассматривать не изолированно, а совместно с абсолютными показателями уровня и прироста.

Для анализа интенсивности изменения во времени одного явления по сравнению с другим рассчитывают коэффициент опережения (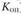). Он представляет собой отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени:

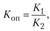
где 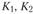- базисные темпы роста соответственно первого и второго рядов динамики.

Коэффициент опережения показывает, во сколько раз быстрее растет уровень одного ряда динамики по сравнению с уровнем другого. При таком сопоставлении темпы должны характеризовать тенденции одного направления. Например, по методологии Росстата общее изменение выпуска товаров и услуг по базовым видам экономической деятельности исчисляется на основе данных об изменении физического объема производства продукции сельского хозяйства, добычи полезных ископаемых, обрабатывающих производств, производства и распределения электроэнергии, газа и воды, строительства, транспорта, розничной и оптовой торговли: за январь-октябрь 2012 г. в процентах к январю-октябрю 2011 г. — 102,9%. При этом оборот розничной торговли увеличился на 6,1%, а грузооборот транспорта — только на 1,8%; коэффициент опережения равен 1,04 (106,1: 101,8).

Показатели динамики с переменной базой сравнения (цепные) используют для выявления типа изменения уровней ряда. В статистической практике в соответствии с показателями динамики различают следующие типы изменений:

• — равномерный рост или снижение (цепные абсолютные приросты одинаковы);
• — ускоренный рост или снижение (цепные приросты систематически увеличиваются по абсолютной величине);
• — замедленный рост или снижение (цепные приросты систематически уменьшаются тоже по абсолютной величине).

Чтобы получить обобщенную характеристику скорости темпов развития изучаемого явления в пределах рассматриваемого периода, рассчитывают средние показатели динамического ряда за единицу времени.