Оценивание модели в условиях гетероскедастичности случайных возмущений

Подход к решению проблемы устранения гетероскедастичности сводится к искусственному преобразованию спецификации модели таким образом, чтобы условие гомоскедастичности выполнялось тождественно. Для понимания этого подхода начнем рассмотрение вопроса с частного случая, когда известны дисперсии случайных возмущений в каждом наблюдении.

Пример. Мы имеем спецификацию модели множественной линейной регрессии, выборку наблюдений за переменными модели для ее идентификации и множество значений дисперсии соответствующих каждому наблюдению. Разделим левую и правую части модели на соответствующее значение стандартной ошибки (корень из дисперсии):

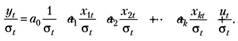(7.8).

Найдем количественные характеристики величины :

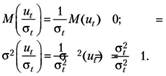
Получилось, что во всех наблюдениях величина 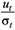имеет нулевое математическое ожидание и постоянную дисперсию. Если ввести новые переменные.

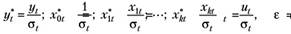(7.9).

и сделать замену переменных, то получим спецификацию модели в виде.

(7.10).

Спецификация (7.10) вновь представляет собой линейную модель множественной регрессии. Для нее необходимо создать выборку наблюдений за переменными (7.9), по ним оценить модель (7.10), убедиться в ее качестве и вновь проверить на гомоскедастичность.

Замечание. В спецификации (7.10) отсутствует свободный от регрессора параметр. При параметре 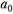появился регрессор .

Слабость такого подхода заключается в том, что им на практике невозможно воспользоваться. Как правило, нет возможности априори оценить ошибку случайных возмущений в каждом уравнении.

Вместе с тем, этот пример подсказывает направление действий для устранения гетероскедастичности. Необходимо задать правило вычисления стандартных ошибок случайных возмущений, разделить на эти ошибки переменные модели и сделать замену переменных. В результате появляется возможность получить модель с гомоскедастичными остатками.

Воспользуемся предположением тестов Голдфельда — Квандта и Спирмена о том, что ошибки случайных возмущений связаны с абсолютными значениями регрессоров. Предположим, что стандартную ошибку случайных возмущений, можно представить в виде.

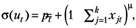(7.11).

где 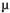 — показатель степени, с помощью которого учитывается возможность нелинейной связи между ошибкой остатка и абсолютным весом регрессоров.

Заменив в (7.8) 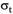на (7.11), получим:

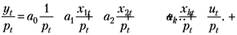(7.12).

Количественные характеристики случайной переменной 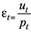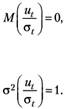Введя новые переменные.

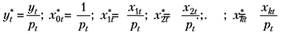(7.13).

и сделав соответствующую замену, вновь получим модель в виде линейного алгебраического уравнения с гомоскедастичными остатками.

Остается открытым вопрос о значении 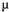. Начинают процесс устранения гетероскедастичности со значения 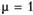. Если при 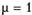модель (7.12) остается гетероскедастичной, то вводится приращение 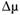(например, 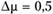) и модель (7.12) проверяется на гетероскедастичность при 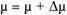Меняя знак и абсолютное значение приращения 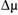, добиваются выполнения соотношений (7.4).

Функцию (7.11) называют весовой функцией. Заметим, что в спецификации модели вида (7.12) значения р, во всех наблюдениях будут равны. Говорят, что преобразование (7.13) выравнивает веса регрессоров во всех наблюдениях.

Пример. При построении модели государственных расходов на образование от объема ВВП выяснилось (рис. 7.1), что модель имеет гетероскедастичные остатки, т. е. гипотеза о выполнении второй предпосылки теоремы Гаусса — Маркова не принимается.

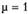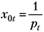Применим описанный выше алгоритм для исправления гетероскедастичности. Примем , вычислим значения для каждого наблюдения и разделим на него значения и введем регрессор (табл. 7.3).

В табл. 7.3 приведены результаты исправления гетероскедастичности: значения преобразованных переменных и проверка полученной модели на гомоскедастичность. Серым выделены фрагменты выборки и значения ESS. Как видно из приведенных данных, исправить гетероскедастичность удалось уже при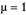

Таблица 7.3

Результаты исправления гетероскедастичности

№. п/п.	Страна.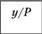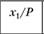
	Люксембург.	0,0510.	0,1499.	0,8501.
	Уругвай.	0,0198.	0,0898.	0,9102.
	Сингапур	0,0259.	0,0810.	0,9190.
	Ирландия.	0,0619.	0,0503.	0,9497.
	Израиль.	0,0825.	0,0456.	0,9544.
	Новая Зеландия.	0,0511.	0,0403.	0,9597.
	Гонконг.	0,0235.	0,0350.	0,9650.	0,0442.	0,0237.	0,0000.
	Венгрия.	0,0440.	0,0432.	0,9568.	0,0106.	0,1558.	#н/д.
	Португалия.	0,0417.	0,0390.	0,9610.	0,8484.	0,0199.	#н/д.
	Чили.	0,0438.	0,0350.	0,9650.	27,9826.	10,0000.	#н/д.
	Греция.	0,0182.	0,0243.	0,9757.	0,0222.	0,0040.	#н/д.
	Финляндия.	0,0532.	0,0190.	0,9810.
	Норвегия.	0,0835.	0,0170.	0,9830.
	Дания.	0,0661.	0,0149.	0,9851.	GQ1=.	1,24 746.
	Австрия.	0,0547.	0,0128.	0,9872.	GQ2=.	0,80 162.
	Югославия.	0,0547.	0,0156.	0,9844.		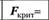2,68 663.
	Швейцария.	0,0517.	0,0097.	0,9903.
	Турция.	0,0235.	0.0147.	0,9853.
	Саудовская Аравия.	0,0547.	0,0085.	0,9915.
	Бельгия.	0,0593.	0,0083.	0,9917.
	Швеция.	0,0897.	0,0080.	0,9920.
	Австралия.	0,0610.	0,0070.	0,9930.
	Аргентина.	0,0359.	0.0065.	0,9935.	0,0585.	— 2,6350.	0,0000.
	Нидерланды.	0,0787.	0,0059.	0,9941.	0,0098.	2,5834.	#н/д.
	Испания.	0,0225.	0,0047.	0,9953.	0,9043.	0,0178.	#н/д.
	Мексика.	0,0291.	0,0053.	0,9947.	47,2491.	10,0000.	#н/д.
	Канада.	0,0720.	0,0038.	0,9962.	0,0301.	0,0032.	#н/д.
	Бразилия.	0,0356.	0,0040.	0,9960.
	Италия.	0,0402.	0,0025.	0,9975.
	Великобритания.	0,0558.	0,0019.	0,9981.
	Франция.	0,0512.	0,0015.	0,9985.
	ФРГ.	0,0473.	0,0012.	0,9988.
	Япония.	0,0592.	0,0010.	0,9990.
	США.	0,0701.	0,0004.	0,9996.

На рис. 7.4 приведены диаграмма рассеяния исходных данных и графики двух моделей: прерывистая линия — модель гетероскедастичная, сплошная линия — модель гомоскедастичная.

Как видно на рис. 7.4 гомоскедастичная модель, в данном случае, проходит ниже гетероскедастичной. Это является следствием того, что при исправлении гетероскедастичности остатков регрессии был выровнен вес всех наблюдений. В исходном состоянии абсолютное значение ВВП для США в разы превосходило соответствующие значения для всех остальных стран, что при формальном применении процедуры МНК приводило к «притягиванию» линии к последней точке. Выравнивание весов всех наблюдений увеличило влияние большинства наблюдений на расположение модельной прямой.

Пример. Оценим и проанализируем на присутствие гетероскедастичности модель зависимости расходов на жилье в зависимости от располагаемого дохода и индекса цен на жилье.

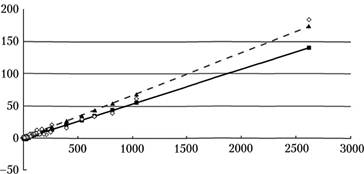
Рис. 7.4. Диаграмма рассеяния исходных данных и графики двух моделей.

В табл. 7.4 приведена выборка данных наблюдений и значения вспомогательной переменно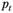й при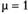

Таблица 7.4

Выборка данных и значения вспомогательной переменной pt.

Спецификация модели имеет вид:

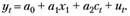
Ограничимся только тестированием модели на гомоскедастичность остатков, опустив анализ качества спецификации.

Приведенные данные отсортированы по переменной 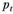В табл. 7.5 данные, по которым проводится анализ, выделены жирным шрифтом.

Таблица 7.5

Результаты построения моделей с помощью функции «ЛИНЕЙН» и значения статистик Голдфельда — Квандта

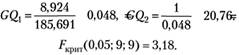
Приведенные результаты свидетельствуют о наличии гетероскедастичности.

Исправление гетероскедастичности начинаем при 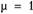В табл. 7.6 приведены данные дня оценки спецификации вида.

(7.14).

Таблица 7.6

В результате тестирования модели (7.14) на гомоскедастичпость с показателем степени весовой функции статистика Голдфельда — Квандта получила значение: GQ= 7,914, что больше критического значения распределения Фишера 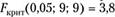Модель осталась гетероскедастичной.

Принимаем приращение для показателя степени весовой функции и проводим построение и анализ модели (7.14) для ряда 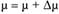. Результаты расчетов приведены в табл. 7.7.

Таблица 7.7

Результаты расчетов

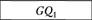1,0.	0,13.	7,91.	3,18.
1,5.	0,20.	4,80.
2,0.	0,32.	3,02.
2,5.	0,53.	1,88.

При дальнейшей вариации абсолютным значением и знаком 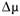методом половинного деления можно добиться выполнения соотношения 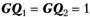. Но в этом необходимости нет, так как в условиях стохастичности достаточно выполнения такой гипотезы в статистическом смысле при заданной доверительной вероятности. Процесс подбора значения? можно остановить на