Оценка параметров закона распределения методом максимального правдоподобия

После изучения главы 4 студент должен:

знать

• • идею метода максимального правдоподобия;
• • понятие и математический смысл функции правдоподобия;
• • алгоритм применения метода максимального правдоподобия для вычисления оценок параметров закона распределения;

уметь

• • составлять функцию правдоподобия для различных задач вычисления оценок параметров законов распределения;
• • применять алгоритм метода максимального правдоподобия для решения конкретных задач;

владеть

• аппаратом метода максимального правдоподобия.

Понятие функции правдоподобия и оценка параметров закона распределения

Пусть имеем выборку 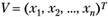из п наблюдений за случайной переменной X, с известным законом распределения вероятностей, функция плотности вероятностей которого 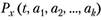, где 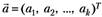параметры функции плотности вероятностей.

Задача: найти значения оценок параметров.

Одним из методов решения поставленной задачи является метод максимального правдоподобия (ММП), который обеспечивает получение, по крайней мере, состоятельных оценок.

В основе метода максимального правдоподобия лежит понятие функции правдоподобия выборки.

Функцией правдоподобия выборки называется функция L, зависящая от параметров закона распределения как от аргументов, и элементов выборки как от параметров и определенная равенством:

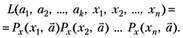(4.1).

Правая часть равенства (4.1) выражает плотность вероятности появления совместного события 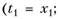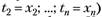, или другими словами, вероятность появления выборки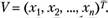

Функция правдоподобия (4.1) обладает следующими свойствами:

• • L — является случайной переменной, так как ее параметры — случайные переменные;
• • все значения функции L неотрицательные, так как это произведение неотрицательных величин.

Идея метода максимального правдоподобия заключается в том, чтобы найти такие значения параметров (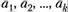), которые обеспечивают получение максимального значения функции правдоподобия.

Так как функция правдоподобия (4.1) отражает вероятность появления в наблюдениях данной выборки, эго означает, что за счет искомых параметров обеспечивается максимальная вероятность появления в наблюдениях данной выборки. Делается предположение, что оценки искомых параметров, которые обеспечивают наибольшую вероятность выборки, являются наилучшими среди всех прочих.

Данное утверждение математически выглядит так:

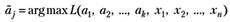(4.2).

или.

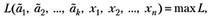(4.3).

где 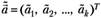 — вектор оценки параметров закона распределения.

Последовательность действий при решении поставленной задачи можно представить в виде следующего алгоритма.

Шаг 1. По известной функции плотности вероятностей формируется функция правдоподобия (4.1).

Шаг 2. Мультипликативная функция (4.1) реорганизуется в аддитивную путем логарифмирования обеих ее частей.

Основание логарифма в общем случае может быть любым. На практике основание логарифма выбирается из условия упрощения результата логарифмирование.

Шаг 3. Поскольку функции L и InL достигают экстремума в одной точке, значения искомых оценок параметров находится в результате решения системы уравнений:

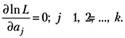(4.4).

Проиллюстрируем процедуру ММП на примере оценки параметров нормального закона распределения вероятностей.

Пример. Пусть мы имеем выборку из и наблюдений за переменной 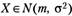. Задача оценить параметры т и 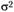методом максимального правдоподобия.

С учетом (3.4) функция правдоподобия принимает вид:

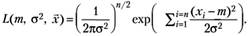(4.5).

Логарифм функции (4.5) по натуральному основанию имеет вид:

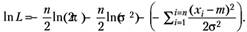(4.6).

Формируется система алгебраических уравнений (4.1.4) путем дифференцирования (4.6) по аргументам т и ?2 и приравнивания их нулю:

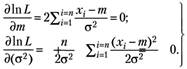(4.7).

Решение системы уравнений (4.1.7) при 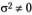имеет вид:

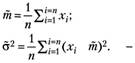(4.8).

Проверим выполнение условия несмещенности для полученных (4.8) оценок. Для этого необходимо вычислить значения математических ожиданий каждой из оценок.

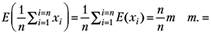(4.9).

Из (4.9) следует, что оценка параметра т нормально распределенной случайной переменной совпадает с его теоретическим значением при любых значениях объема выборки и, т. е. полученная оценка несмещенная.

Можно показать, что:

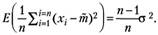(4.10).

Видно, что условие несмещенности для параметра 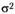достигается только при больших объемах выборки и. Следовательно, оценка (4.8) второго параметра нормально распределенной случайной является асимптотически несмещенной.

Выше рассмотрен вопрос оценки параметров законов распределения, но задача эконометрики — научиться вычислять оценки параметров линейной модели. Рассмотрим, как воспользоваться ММП для оценки линейной эконометрической модели.

Для упрощения выкладок рассмотрим частный случай линейной модели — уравнение парной регрессии:

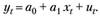(4.11).

Так же предполагаем, что для расчета искомых параметров в нашем распоряжении выборка пар переменных (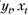) объемом п.

Пусть случайное возмущение и является нормально распределенной случайной переменной с параметрами т = 0, 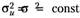. Из (4.11) следует, что.

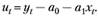
Тогда функцию плотности вероятностей нормального закона распределения для случайной переменной и принимает вид:

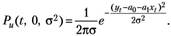(4.12).

Неизвестные параметры модели (4.11) стали параметрами функции плотности вероятностей (4.12). Функция правдоподобия (4.1) принимает вид:

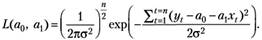(4.13).

После логарифмирования по натуральному основанию получим:

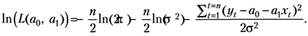(4.14).

Приравняв нулю частные производные по а1 и а0 функции (4.14), получим систему алгебраических уравнений для вычисления значений оценок искомых параметров:

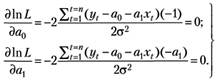(4.15).

Умножив уравнения (4.15) на 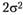, и, сделав несложные преобразования, получим систему алгебраических уравнений для вычисления искомых оценок:

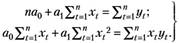(4.16).

Решив систему уравнений (4.16) относительно неизвестных параметров 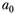и 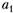, получим их несмещенные значения.