Системы счисления для числовой информации

Для представления чисел выбирается система счисления, которая характеризуется алфавитом и структурой кода. Символы для изображения чисел составляют цифровой алфавит. В мире существует несколько цифровых алфавитов для различных систем счисления:

¦ двоичный — цифры 0 (ноль) и 1 (один);

¦ восьмеричный — цифры 0 (ноль), 1 (один), 2 (два), 3 (три), 4 (четыре), 5 (пять), 6 (шесть), 7 (семь);

¦ десятичный — арабские цифры 0 (ноль), 1 (один), 2 (два), 3 (три), 4 (четыре), 5 (пять), 6 (шесть), 7 (семь), 8 (восемь), 9 (девять);

¦ шестнадцатеричный — арабские цифры (0−9) и буквы А (число 10), В (число 11), С (число 12), D (число 13), Е (число 14), F (число 15);

¦ римский — основные цифры I (1), X (10), С (100), М (1000) и вспомогательные V (5), L (50), D (500), соответствующие «половинному» значению основных цифр.

Система счисления может быть позиционной или непозиционной.

Позиционная система счисления

Код числа имеет разрядную структуру, местоположение цифры в разряде кода влияет на значение числа. Для позиционной системы счисления выбирается основание, цифровой алфавит. Число может содержать как целую, так и дробную часть. Все разряды кода числа пронумерованы согласно десятичной системе счисления. Номера разрядов от 0 и выше соответствуют целой части числа, номера разрядов меньше 0 соответствуют дробной части числа (рис. 3.2).

Рис. 3.2. Позиционная система счисления Значение числа в позиционной системе счисления вычисляется по формуле.

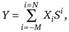
где 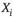- значение i-го разряда в коде числа;

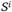- весовой коэффициент i-го разряда кода числа.

Для каждой системы счисления определяется множество значени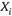й и .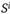

Существует зависимость плотности записи информации (количества символов, необходимых для изображения значения числа, — длины кода числа) от основания системы счисления. Для определения оптимального основания системы счисления, которое минимизирует длину кода числа, используют следующую формулу:

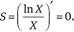
Решением уравнения является значение X = 2,718 281 828, т. е. из целочисленных систем счисления наибольшей плотностью записи информации обладает троичная система счисления. Наиболее распространены позиционные системы счисления с основаниями 2, 8, 10 и 16. Аналогично в восьмеричной системе счисления с основанием 8 используются цифры 0, 1, 2, 3, 4, 5, 6, 7, весовой коэффициент разряда числа равен 8 в n-й степени. Шестнадцатеричная система счисления с основанием 16 использует десять цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и шесть букв: А, В, С, D, Е, F; весовой коэффициент разряда числа равен 16 в n-й степени.

Максимальное целое число, которое может быть представлено в т разрядах,.

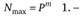
Минимальное значащее, не равное нулю, число, которое можно записать в s разрядах дробной части,.

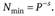
Таким образом, можно записать всего 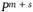разных чисел, где Р — основание системы счисления.

Десятичная система счисления. Традиционная десятичная система счисления использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а каждый разряд имеет весовой коэффициент 10 в n-й степени. Это наиболее употребляемая во внемашинной сфере система счисления.

Число 29,5625 можно представить в разложении:

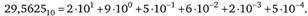
Двоичная система счисления. В двоичной системе счисления с основанием 2 используются только цифры 0 и 1, а весовой коэффициент разряда числа равен 2 в n-й степени (п принимает положительное, нулевое или отрицательное целое значение).

Соответствие чисел в десятичной и двоичной системах счисления:

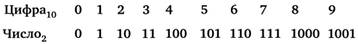
Для перевода двоичных чисел в десятичную систему счисления требуется представить двоичное число позиционно.

Пример

Двоичное число 11 101,10012 представляется следующим образом:

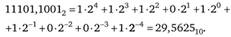
Для обратного перевода десятичного числа в двоичную систему счисления следует делить исходное число на основание двоичной системы счисления (2). Остаток от деления используется как значение текущего разряда двоичного числа. Операция деления и нахождения остатка соответствует вычислению по модулю 2. Это преобразование применяется много раз, пока не будет получено нулевое частное от деления.

Пример

Перевод десятичного числа 29 в двоичное представление:

(29) mod 2 = 1, частное отделения 14, 0-й разряд содержит остаток отделения 1;

(14) mod 2*0, частное от деления 7, 1-й разряд содержит остаток отделения 0;

(7) mod 2*1, частное от деления 3, 2-й разряд содержит остаток отделения 1;

(3) mod 2*1, частное от деления 1, 3-й разряд содержит остаток отделения 1;

(1) mod 2 = 1, частное от деления 0, 4-й разряд содержит остаток отделения 1.

Если частное от деления равно 0, то перевод целой части десятичного числа в двоичную систему счисления закончен. Таким образом, 2910 = 111 012.

Для перевода дробной части десятичного числа в двоичное представление осуществляется последовательное умножение дробной части десятичного числа на основание системы счисления — число 2. Целая часть результата умножения соответствует очередному разряду дробной части двоичного числа. Далее используется полученная дробная часть результата для следующего умножения на основание системы счисления — число 2. Операция умножения выполняется до достижения требуемой точности результата либо пока дробная часть результата не будет равна 0.

Перевод 0,562 510 в двоичное представление:

• 0,5625 • 2 = 1,125, разряд двоичного числа с номером -1 равен 1; отбрасываем целое число и повторяем умножение;
• 0,125 • 2 = 0,25, разряд двоичного числа с номером -2 равен 0;
• 0,25 • 2 = 0,5, разряд двоичного числа с номером -3 равен 0;
• 0,5 • 2 = 1,0, разряд двоичного числа с номером -4 равен 1.

Поскольку дробная часть результата равна 0, то перевод десятичного дробного числа в двоичное представление закончен и 0,562 510 = 0,10 012.

В двоичной системе счисления над числами можно выполнять арифметические операции сложения, вычитания, умножения и деления.

Сложение чисел выполняется согласно следующим правилам: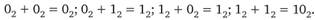

Вычитание чисел осуществляется по следующим правилам:

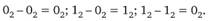
При вычитании 1 из 0 следует учитывать, что:

¦ если имеются старшие разряды числа, заимствуется 1 и выполняется вычитание обычным образом, например 1002 — 0102 = = 0102;

¦ если число не содержит старших разрядов, вычитание заменяется сложением с вычитаемым, представленным в инвертированном коде.

Умножение чисел выполняется стандартным поразрядным способом, при этом:

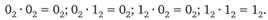
Деление чисел производится стандартным способом, например разделить 10 012 на 1102 (910 разделить на 610):

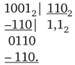
Форматы представления двоичных чисел. Существуют как целые, так и действительные числа (с плавающей точкой). Для представления целых чисел в компьютере в двоичной системе счисления используются прямой, обратный и дополнительный коды.

Прямой код предусматривает, что знак числа кодируется нулем для положительных и единицей для отрицательных чисел. Например, для положительного числа 710 прямой код равен 111; для отрицательного числа — 710 прямой код равен 1 000 111.

Обратный код для положительных чисел совпадает с прямым кодом, а для отрицательных получается из прямого кода инверсией значений всех разрядов кода, кроме знакового. Например, для отрицательного числа — 710 обратный код равен 1 111 000. Обратный тип кода позволяет унифицировать сложение и вычитание двоичных чисел. При сложении чисел в обратном коде количество разрядов результата может превысить стандартную длину. В этом случае происходит циклический перенос разряда переполнения (старшего разряда), его сложение с младшим разрядом кода, например:

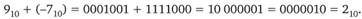
Дополнительный код (дополнение до 2) для положительных чисел совпадает с прямым кодом, а для отрицательных получается из обратного кода сложением с 1. При использовании дополнительного кода упрощается суммирование, не возникает необходимости в циклическом переносе из старшего разряда в младший. Например, число -710 в дополнительном коде 1 111 001, результат сложения 910 + (-710) = 1 001 + + 1 111 001 = 10 (разряд переполнения отбрасывается).

Действительное число с плавающей точкой представляется в следующем формате:

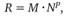
где М — мантисса;

N — основание системы счисления;

Р — порядок (целая степень).

В ЭВМ используют нормализованное представление числа с плавающей точкой, мантисса находится в диапазоне от 0,1 до 1 (т.е. мантисса не превосходит 1), первая значащая цифра мантиссы не равна 0 для любой системы счисления, например:

• 12.345 = 0.12 345 -104 — ненормализованное десятичное число;
• 12.345 = 1234.5 •10~2 — ненормализованное десятичное число;
• 12.345 = 0.12 345 •102 — нормализованное десятичное число.

Мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся), например, как число 12 345. Для восстановления истинного значения числа используется порядок.

Восьмеричная система счисления. В этой системе счисления используется набор цифр 0−7.

Пример

Выполнение вычислений в восьмеричной системе счисления: 77 728 + 5274″ = 152 668, или 409 010 + 274 810 = 683 810;

• 77 728 — 52 748 = 24 768, или 409 010 — 274 810 = 134 210;
• 77 728 • 52 748 = 52 676 308, или 409 010 • 2748,0 = 112 932 010.

Для преобразования чисел из восьмеричной системы счисления в двоичную достаточно записать каждую цифру числа в двоичном коде: 77 728 = 1 111 111 110 102; 52 748 = 1 010 101 111 002.

Арифметические операции над числами, переведенными из восьмеричной системы счисления в двоичную, выполняются обычным образом, а полученный результат преобразуется в восьмеричную систему счисления путем перевода триад двоичного кода в цифры для восьмеричной системы счисления.

Пример

111 111 1110 102 + 101 010 1111 002 = 11 010 101 10 1102. Результат сложения равен 15266g.

Шестнадцатеричная система счисления. Для шестнадцатеричной системы счисления используется расширенный алфавит обозначения цифр: цифры 0−9 и буквы, А (А16 = 1010), В (В16 = 1110), С (С16 = 1210), D (D16 = 1310), Е (Е16 = 1410), F (F16 = 1510).

Пример

Выполнение вычислений в шестнадцатеричной системе счисления: FFA16 + АВС16 = 1АВ616, или 409 010 + 274 810 = 683 810;

FFA16 — АВС16 = 53Е16, или 409 010 -274 810 = 134 210;

FFA16 • АВС16 = AB7F98)6, или 409 010 • 274 810 = 112 932 010.

Числа в шестнадцатеричной системе счисления можно представить в другой системе счисления следующим способом:

¦ для двоичной системы счисления следует двоичное представление числа разбить на тетрады двоичных разрядов, например число FFA16 имеет вид 11 111 1111 0102.

¦ для восьмеричной системы счисления требуется двоичное представление шестнадцатеричного числа разбить на триады двоичных разрядов, например число FFA16 имеет вид 111 111 1110 102 или 77 728.

Непозиционная система счисления

Для непозиционной системы счисления отсутствует строго определенная структура кода числа. Обычно для обозначения чисел вводятся специальные знаки, количественное значение которых всегда одинаково и не зависит от их места в записи числа. Примером такой системы является запись чисел римскими цифрами (табл. 3.1).

Таблица 3.1. Пример непозиционной системы счисления.