Фильтрация записей таблицы

Фильтрация — это отбор записей списков по заданным условиям.

Различают автофильтрацию для простейших условий отбора записей и фильтрацию с помощью расширенного фильтра для сложных условий отбора. Условия фильтрации используются встроенными функциями для работы с базой данных Excel.

Автофильтрация

Курсор устанавливается в область списка, по команде меню Данные, Фильтр, Автофильтр имена полей списка преобразуются в элемент управления «поле со списком». Список содержит до 999 уникальных значений ячеек поля и следующие опции отбора записей:

¦ Все — снять фильтр, вывод всех записей списка без ограничений;

¦ Первые 10 — ограничение на число выводимых записей списка;

¦ Условие — логическое выражение, задающее условие вывода записей списка;

¦ Точное значение — выбор записей, содержащих только указанное значение.

Выбор опций производится после нажатия кнопки Ў в заголовках столбцов.

Условия фильтрации задаются в виде точного значения или условного выражения (рис. 12.14). Точное значение для сравнения выбирается из раскрывающегося списка поля. Условие состоит из одного или двух предложений, связанных логической связкой И или ИЛИ.

Рис. 12.14. Задание условий для пользовательского автофильтра.

Расширенный фильтр

Расширенный фильтр задается командой меню Данные, Фильтр, Расширенный фильтр. Вне основного списка на листе списка или другом листе той же самой или иной рабочей книги формируется диапазон условий, который включает в себя: имена столбцов условий, строки условий для отбора записей.

Состав полей столбцов списка в диапазоне условий указывается в произвольном порядке. Например, на рис. 12.15 приведен диапазон условий расширенного фильтра для компьютеров, у которых емкость жесткого диска составляет не менее 4,3 Гбайт, стоимость — не выше 400 долл., а также компьютеров с видеокартой типа 4 Mb AGP.

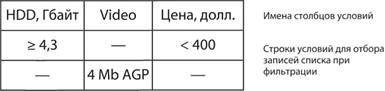
Рис. 12.15. Диапазон условий расширенного фильтра Условия фильтрации, размещенные в одной строке диапазона, объединяются логической функцией И; условия, заданные в разных строках, — функцией ИЛИ. Пустые строки условий не допускаются.

При вызове команды меню Данные, Фильтр, Дополнительно выводится диалоговое окно Расширенный фильтр (рис. 12.16).

Рис. 12.16. Диалоговое окно команды Расширенный фильтр В этом случае указывается местоположение результата фильтрации списка: Фильтровать список на месте или скопировать в другую область рабочего листа, или другой лист текущей или другой открытой рабочей книги — Скопировать результат в другое место. В поле Исходный диапазон указывается диапазон ячеек списка (имя блока), в поле Диапазон условий — диапазон ячеек области критериев (имя блока). В поле Поместить результат в диапазон дается ссылка на верхнюю левую ячейку выходного диапазона. Если требуется отобрать записи с неповторяющимися значениями фильтруемых полей, устанавливается флажок Только уникальные записи.

Вычисляемые условия

Диапазон условий может содержать вычисляемые критерии. В этом случае он заполняется в соответствии со следующими правилами:

¦ заголовок столбца вычисляемого критерия диапазона условий не должен совпадать с именами полей списка (может не заполняться);

¦ в строке условия вводится формула, которая вычисляет логическую константу (ИСТИНА, ЛОЖЬ) по отношению к первой записи списка;

¦ формула содержит ссылки на ячейки списка. В левой части формулы (до знака сравнения) ссылки на ячейки списка должны быть относительными, в правой части формулы — абсолютными. Ссылки на ячейки вне списка должны быть всегда абсолютными.

Например, для компьютеров, цены которых не выше средней, сниженной на заданный процент, имя столбца ЦЕНА1 не совпадает с именами полей списка. Формула фильтрации имеет логический вид:

=G2<=CP3HA4 ($G$ 2:$G$ 11)*(1 — $N$ 4).

Левая часть формулы (G2) — относительная ссылка на первую ячейку столбца Цена. Правая часть формулы использует встроенную функцию СРЗНАЧ по диапазону ячеек столбца Цена. $G$ 2:$G$ 11 — абсолютные ссылки на диапазон ячеек блока. Процент снижения цены находится в ячейке $N$ 4 — абсолютная ссылка, так как ячейка находится вне списка.

Общий вид вычисляемого критерия представлен на рис. 12.17.

Рис. 12.17. Общий вид вычисляемого критерия.