Понятие функции комплексного переменного, ее предел и непрерывность

Терминология и символика здесь и далее используется лишь для обычной комплексной плоскости С; случай расширенной плоскости не рассматривается.

Говорят, что на множестве Еа С задана функция, если каждому числу z е Е поставлено в соответствие одно комплексное число w или некоторая их совокупность. Пишут: w=f (z), zeE. Функция называется однозначной, если каждому zeE сопоставляется только одно число м>; в противном случае функция называется многозначной. Например функция w = z² одозначиая в С, а функция w=Vz многозначная (точнее, двузначная). Подробное изложение многозначности в данном пособии опущено; мы ограничимся в дальнейшем рассмотрением лишь нескольких примеров. В этой главе и в следующей предполагается однозначность рассматриваемых функций.

Пусть задана функция v = f (z), zeE со значениями в комплексной плоскости. Обозначим z = x + yi, w=u + iv. Если в действительном одномерном анализе функциональную зависимость у = f (x) можно визуализировать (построить график функции), то аналогичный прием дтя функции f (z) не удастся — ведь пространство переменных (x, y, u, v) чстырсхмсрнос, недоступное нашему трехмерному восприятию. Вследствие этого используют так называемый рельеф (ландшафт) фкнкции. Это — поверхность модуля функции в трехмерном пространстве (*, д>,| w|), она иногда позволяет составить наглядное представление о поведении некоторых конкретных функций. Например, рельеф функции w = z² — это параболоид с уравнением | w=x² + у². Сделайте чертеж самостоятельно.

Чаще всего для геометрического истолкования функции рассматривают два экземпляра комплексной плоскости: С. — (плоскость аргумента), в которой изображаются числа zeE, и другая плоскость С_и., в которой изображаются значения функции. В наиболее важных на практике случаях кривые при отображении / переходят в кривые, а области — в области. Однако это не всегда так. Например, функция w = Rer область С_х отображает лишь на действительную ось плоскости С_и.

Ясно, что функцию w = f (z) комплексного переменного z = x + yi можно представить в виде w = u (x, y) + iv (x, y) с действительнозначными функциями двух действительных переменных. При этом, по определению, функция и=и (х, у) — это действительная часть функции jz), a v = v{x₄y) — ее мнимая часть.

Пример. Выделить действительную и мнимую части функции _ 1.

w = z —.

Z

Решение. Имеем 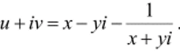. Здесь правая часть примет вид.

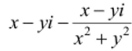. Следовательно,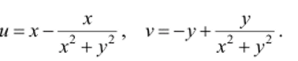

В реальных приложениях комплексного анализа чаше всего роль множества Е играет некоторая область, которую обозначаем через D (от английского domain). Часто встречаются следующие задачи.

1. B D задана кривая L. Каков ее образ К при отображении^[1]

В решении второй задачи возможен следующий прием. Представим себе область D с С_: образованной «заметанием» кривой L. Смотрим ее образ.

К и наблюдаем, какую область он «заметает» в C_w.

Пример. Рассмотрим функцию w = z.

• 1). Найдем, в какую кривую она отображает вертикаль в С_: х = а * 0.
• 2). Каков образ полосы, лежащей между вертикалями х = 1 и х = 2? Решение. 1). Имеем: w=(x + iy) = х +2xyi-y => и =ху, v-2xy.

При х = а тогда иа¹ -у, v = 2ау. Это и есть параметрические уравнения кривой К, в которых параметром является y&R. Исключив его из уравнений, получим.

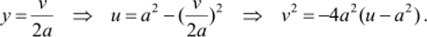
Следовательно, данная вертикаль перешла в параболу с этим уравнением. Сделайте самостоятельно чертежи при а = 1, а = 2.

2). Полоса, заключенная между прямыми х = 1, х = 2 (рис.8а)), получается «заметанием» прямой х = а, когда а изменяется от 1 до 2. При этом парабола.

v =-4а (и-а) «заметает» криволинейную полосу на рис.86).

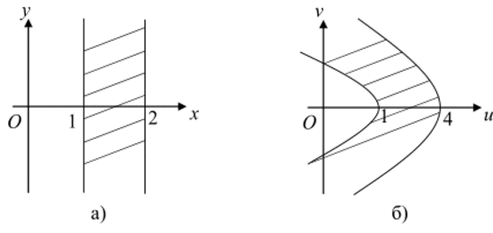
Рис. 8.

В решениях задач 1 и 2 часто используются полярные координаты.

Пример. Показать, что функция w = z² преобразует луч, выходящий из начала координат С_г, в луч, выходящий из начала координат С_н., но при этом угол наклона его к действительной оси удваивается.

Решение. Точка z = /*(cosM-/sinf) опишет луч, если t = const, r> 0. Так как w = г²(cos 2t + isin 2/), то видно, его аргумент равен 2/. Следовательно, точка w опишет луч с углом наклона, вдвое большего первоначального.

Отсюда как следствие получим, что угол с вершиной в начале координат преобразуется в угол удвоенного раствора. Например, первая четверть {Rez > 0, Imz > 0} переходит в верхнюю полуплоскость, а полуплоскоть {lmz>0} преобразуется в плоскость с разрезом вдоль неотрицательной части действительной оси С_н.

В курсе действительного одномерного анализа рассматривались два эквивалентных определения предела функции в точке: на языке e-S (по Коши) и на языке последовательностей (по Гейне). Они дословно переносятся в комплексный анализ. Приведем их.

Пусть функция /(z) определена в проколотой окрестности U* точки ²о;

• 1. Число с называется пределом функции в этой точке, если для любого ?>0 существует такое S> 0, что из неравенств 0<|z-z_o|f (z)-c
• 2. Число с называется пределом функции в точке z₀, если для любой последовательности комплексных чисел z_neU сходящейся к z₀, соответствующая последовательность значений функции f (z_n) сходится к с*.

Равносильность этих определений здесь не доказывается; следует повторить тс же рассуждения, что и в действительном анализе. В обоих определениях используется знакомая запись.

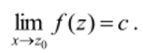
Заметим, что из второго определения предела следует такой признак несуществования предела:

если можно найти такие две последовательности аргумента, удовлетворяющие условиям этого определения, что соответствующие последовательности значений функции имеют различные пределы, то функция в точке z₀ предела нс имеет.

Пример. Имеет ли предел в точке z₀ = 0 функция.

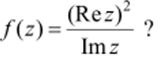
Решение. Рассмотрим последовательности.

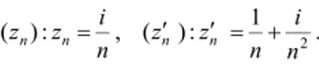
Очевидно, обе они сходятся к нулю. Но последовательность значений функции по первой из них сплошь состоит из нулей и, следовательно, сходится к нулю; на второй последовательности значения функции состоят из единиц, поэтому последовательность ее значений сходится к единице. Из неравенства 0 * 1 делаем вывод: в рассматриваемой точке данная функция предела не имеет.

Так как принятое определение предела функции читается в точности так, как и в действительном анализе, и алгебраические действия над комплексными функциями проводятся по тем же правилам, как и над действительными, то в комплексный анализ автоматически переносятся элементарные теоремы о пределах (о пределе суммы и др.) — мы не останавливаемся на их формулировках и доказательствах.

Понятие предела обобщается на случаи, когда z или f (z) стремятся к бесконечности. В этих случаях надо заменить окрестности обыкновенных точек окрестностями бесконечно удаленной точки. Например, запись lim f{z) = c означает, что для любого е>0 найдется такое ?>0, что при.

z> S будет f{z)-c Очевидно, что lim f (z) = c в том и только в том Г-КЮ случае, когда

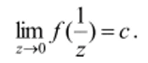
Пример. Найти предел.

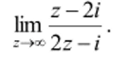
Решение. Заменяя z на -, сведем задачу к вычислению предела.

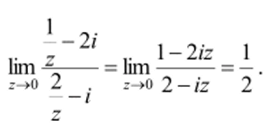
Как и в действительном анализе, функция w = f (z) называется непрерывной в точке z₀ € С, если.

• 1) она определена в окрестности этой точки;
• 2) существует конечный предел функции в этой точке;
• 3) этот предел равен /(z₀).

По соображениям, о которых говорилось выше, в комплексный анализ переносятся элементарные теоремы о непрерывных функциях в точке (непрерывность суммы и др.). Очевидно, что функция непрерывна в точке ^zo ⁼ *0 ⁺ О^;о тогда и только тогда, когда в точке (дг₀, у₀) непрерывны в смысле двумерного действительного анализа ее действительная и мнимая части. Это часто упрощает проверку непрерывности.

Пример. Доказать, что функция f (z)=z² z непрерывна в каждой точке комплексной плоскости.

Решение. Полагая z = x + yi_t получим f (z) = (x²+y²)(x + yi). Действительная и мнимая части функции равны соответственно.

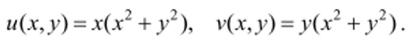
Они обе непрерывны как функции двух действительных функций в любой точке (*,>>) е R². Отсюда приходим к выводу о непрерывности f (z) в любой точке плоскости.

В заключение приведем небольшую подборку задач по рассматриваемой теме.

3.1. Пусть z = x + yi. Подвергнуть прямую х+у = 1 преобразованиям.

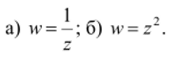
3.2. В какую область функция w = — преобразует полосу 1 < Rez < 2 ?

z

3.3. Запишите на языке «e-S» равенства.

a) lim /(z) = оо {а е С); б) ton /(z) = со.

z—*a ос.

3.4. Установить, имеют ли данные функции предел в указанных точках. Если предел существует, найти его.

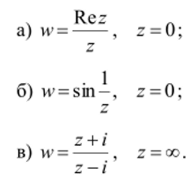
3.5. Является ли функция w=argz непрерывной в точке z =—1 ?

• [1] Как найти образ области при этом отображении? В первой задаче обычно кривая задается параметрически: х = x (t у = y (t). Тогда ее образ К имеет параметризацию и = u (x (t), y{t) v = v (jt (f),.KO). В решении второй задачи часто поступаюттак: область D представляют себе как образованную «заметанием» какой-нибудь кривой, зависящей от параметра. Например, круг |z|