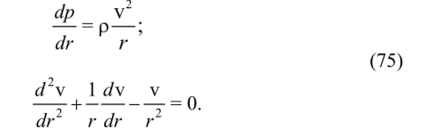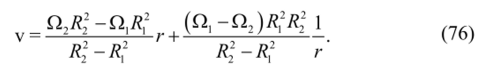Течение Куэтта между вращающимися цилиндрами

Рассмотрим течение вязкой несжимаемой жидкости между двумя бесконечно длинными соосными цилиндрами, вращающимися вокруг общей оси с угловыми скоростями Q, и О, (рис. 12).

Выберем цилиндрическую систему координат с осями z, г, <�р. Поскольку все значения координаты z физически равноправны, то компоненты скорости не могут зависеть от z. Равноправие направлений «вверх» и «вниз» по оси z означает, что осевая компонента скорости v. равна нулю. Условие несжимаемости жидкости означает, что радиальная компонента скорости у также равна нулю. Следовательно, из всех компонент скорости не равна нулю только полярная компонента v, которую для краткости мы будем обозначать v. Эта компонента может зависеть только от расстояния г до оси цилиндров.

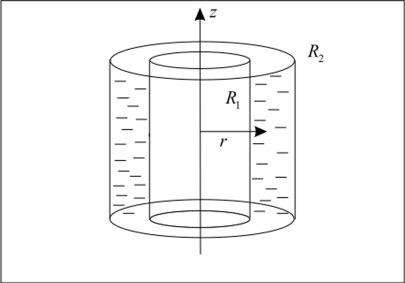
Рис. 12.

Уравнение Навье — Стокса в цилиндрических координатах в рассматриваемом случае дает два уравнения:

Второе из этих уравнений является однородным уравнением Эйлера. Его решение:

Постоянные интегрирования С, и С, находятся из граничных условий прилипания на внутреннем и внешнем цилиндрах, т. е. при r = R_i2 выполняется v = D._l 2R_i 2 соответственно. В результате.

Рассмотрим несколько важных частных случаев.

• 1. Q, = Q, = Q. Отсюда v = Qг, т. e. жидкость вращается как целое вместе с цилиндрами.
• 2. Внутреннего цилиндра нет (R_t = 0). В этом случае v = Q, r, т. с. жидкость вращается как целое вместе с внешним цилиндром.
• 3. Нет внешнего цилиндра (Q, =0, R₂ =оо). Из уравнения (76) получаем v = О,/?,² / г.