Необходимость и возможность получения пары сигналов: когерентного и квадратурного

Путем сдвига времени преобразования на половину периода мы получили сдвиг преобразованного сигнала на ту же половину периода. Аналогично, вводя сдвиг на четверть и на три четверти периода, мы можем получить сигналы разностной частоты с таким же сдвигом фаз. Аналогичным образом, вычитая один из другого, можно получить второй сигнал, который имеет сдвиг фаз на половину периода по отношению к ранее полученному сигналу.

Эта пара сигналов называется когерентным (синхронным) и квадратурным сигналами соответственно, а в совокупности они называются аналитическим сигналом.

Аналитический сигнал можно трактовать как проекции вращающегося вектора на оси абсцисс и ординат соответственно. В этом случае вычисление фазы осуществляется из простого геометрического соотношения. Фаза угла наклона вектора равна арктангенсу отношения квадратурной компоненты к когерентной либо арккотангенсу обратного отношения.

Как видим, аналитический сигнал легко получить и легко использовать для вычисления фазы.

Проиллюстрируем это на сигналах, получаемых математическим моделированием.

Ранее, как показано на рис. 18.17, получен когерентный сигнал разностной частоты. С помощью такой же модели, отличающейся только сдвигами фаз сигналов, подаваемых на УВХ, легко получить квадратурный сигнал. Нарис. 18.22 показаны два сигнала — когерентный и квадратурный. Разница между ними состоит только в сдвиге фаз моментов взятия отсчетов входной частоты, общий сдвиг второго канала по отношению к первому составляет четверть периода взятия частоты. Здесь в каждом канале использована компенсация запаздывания.

Теперь остается только из когерентного и квадратурного сигналов вычислить разность фаз.

Вместо вычисления арктангенсов можно построить график изменения вектора аналитического сигнала в фазовой плоскости. Это достаточно наглядно иллюстрирует возможности определения фазы. Действительно, любая точка в фазовой плоскости отмечает текущее в данный момент времени положение конца вектора, который представлен своими проекциями и виде аналитического сигнала. Если начало координат соединить с этой точкой, получим.

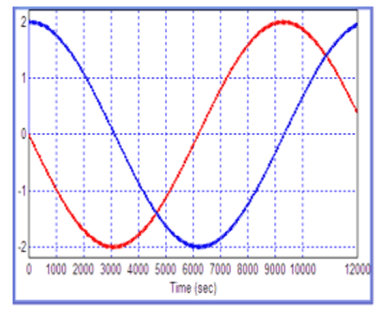
Рис. 18.22. Два сигнала — когерентный и квадратурный (разность фаз между ними — четверть периода)

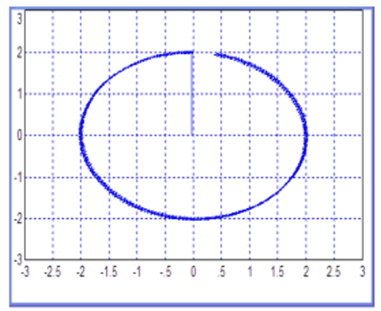
Рис. 18.23. Фазовый портрет, полученный из сигналов, показанных на рис. 18.22

сам вектор, а угол между этим вектором и осью абсцисс и есть искомая фаза. Преимущество такого представления состоит в том, что можно определять угол во всех четырех квадрантах и даже в большем диапазоне, отслеживая поворот вектора. Если получаем круг (или при неравенстве масштабов по осям — эллипс), то это идеальный результат обработки сигнала. Наличие шумов в сигнале даст некоторые отклонения графика от идеального круга. Это породит некоторые девиации вектора по длине и по углу его поворота, но если при подобных девиациях конец вектора не проходит через начало координат вследствие шумов, то измерение фазы будет осуществляться непрерывно и без срывов слежения за фазой.

На рис. 18.23 показан фазовый портрет, полученный из этих сигналов. В этом случае один из сигналов откладывается по оси абсцисс, а другой — по оси ординат. На рис. 18.24 показан такой же сигнал, полученный в присутствии шумов, на рис. 18.25 — такой же сигнал при еще большем увеличении шумов, а именно при стандартном отклонении в два раза большем, чем на рис. 18.24.

Из рис. 18.25 видно, что измерение фазы было бы осуществлено без сбоев. Входной сигнал для этого случая показан на рис. 18.26. Дальнейшее увеличение шумов вдвое также не приводит к срыву измерений, что видно из рис. 18.27, где показан соответствующий фазовый портрет. Входной сигнал для этого случая показан на рис. 18.28. Полученные в результате обработки сигналы в виде функций времени по отдельности, когерентная и квадратурная компоненты, показаны на рис. 18.29. Это те же сигналы, что показаны на рис. 18.27 в фазовой плоскости.

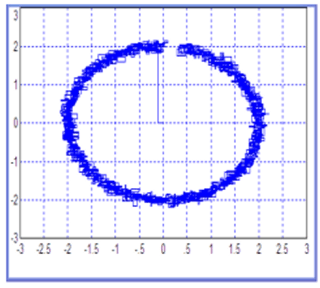
Рис. 18.24. Такой же сигнал, полученный в присутствии шумов

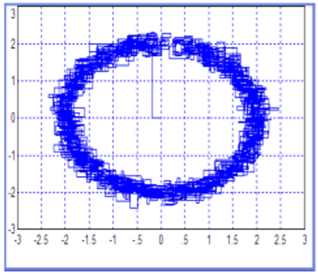
Рис. 18.25. Такой же сигнал при увеличении шумов в два раза большем, чем на рис. 18.24

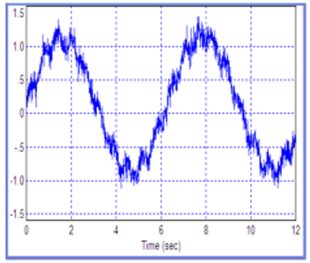
Рис. 18.26. Входной сигнал для случая фазового портрета, полученного на рис. 18.25

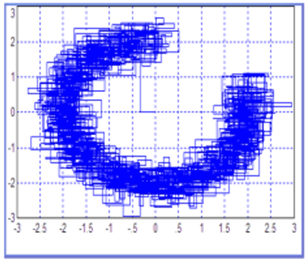
Рис. 18.27. Такой же сигнал при увеличении шумов в четыре раза большем, чем на рис. 18.24

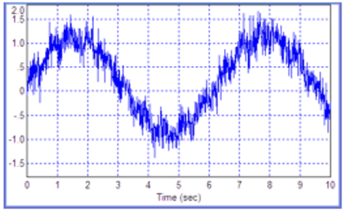
Рис. 18.28. Входной сигнал для случая фазового портрета, полученного на рис. 18.27

Рис. 18.29. Тс же сигналы, что па рис. 18.27, когерентный и квадратурный, но в виде функций времени

Тот факт, что на рис. 18.27 график остается далеко от начала координат, кроме начального участка, говорит о том, что вектор, начало которого лежит в начале координат, а конец движется вдоль этого графика, не изменяет скосго угла поворота слишком резко, т. е. его угол как функция времени поворота не претерпевает разрывов.