Спрос на труд конкурентной фирмы

Рассмотрим конкурентную фирму, т. е. фирму, которая не может влиять на рыночную цену производимого продукта. В этом случае рыночная цена продукта рассматривается как неизменная, заданная величина.

Спрос фирмы на труд при некоторой ставке заработной платы равен величине затрат труда, обеспечивающей фирме максимальную прибыль. Прибыль конкурентной фирмы выражается следующей формулой: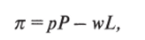

где р — фиксированная цена продукта;

Р— производственная функция фирмы;

w — ставка заработной платы;

L — затраты труда (численность персонала).

Для определения условия максимизации прибыли продифференцируем функцию прибыли и приравняем ее производную нулю. Получим соотношение, задающее функцию спроса на труд конкурентной фирмы:

где MP_L — предельный продукт труда. Правую часть данного равенства называют стоимостью предельного продукта труда, из него следует, что кривая спроса на труд конкурентной фирмы совпадает с графиком функции стоимости предельного продукта труда.

Графики названных функций совпадают, однако сами функции не являются тождественными: функция спроса на труд задана на множестве значений ставок заработной платы, а функция стоимости предельного продукта труда — на множестве значений затрат труда. Иными словами, функция спроса на труд конкурентной фирмы является обратной к функции стоимости предельного продукта труда.

Поскольку в рассматриваемой модели рыночная цена продукта фиксирована, ее часто принимают равной единице. Тогда кривая спроса на труд конкурентной фирмы совпадает с графиком предельного продукта труда, а сама функция спроса является обратной к функции предельного продукта труда.

Пример 1. Производственная функция конкурентной фирмы задана формулой 4L⁰*⁵, цена продукта равна 10. Определим формулу спроса на труд и рассчитаем объем спроса при ставке заработной платы, равной 4. Для этого умножим производную производственной функции на цену продукта. Тогда, согласно формуле (10.1), получим:

Объем спроса на труд при ставке заработной платы 4 равен 400:4²=25.

Пример 2. Производственная функция конкурентной фирмы задана в табл. 10.1. Во второй строке таблицы рассчитаны значения предельного продукта труда посредством вычитания «соседних» значений производственной функции. Затраты труда измеряются количеством работников фирмы, цена продукта равна единице. Тогда спрос на труд составит: при ставке заработной платы 10 ед. — 5 человек, при ставке заработной платы 11 ед. — 4 человека, и т. д.

Таблица 10.1

Спрос на труд конкурентной фирмы (пример).

Неценовыми факторами спроса на труд называют причины, вызывающие изменение кривой спроса на труд. Для конкурентной фирмы таковыми являются:

• • цена продукта. С увеличением цены продукта кривая спроса на труд сдвигается вправо—вверх (спрос увеличивается), с уменьшением цены — влево—вниз (спрос сокращается);
• •технология производства. Замена старой технологии на более продуктивную может привести как к снижению спроса на труд, так и к его увеличению. Покажем это на примере.

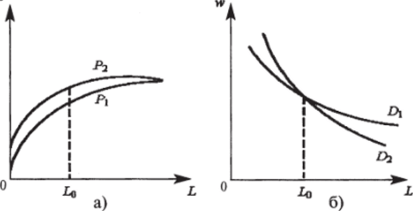
Рис. 10.1. Влияние технологических изменений на спрос фирмы на труд

На рис. 10.1а старая и новая производственные функции обозначены через Р и Р*1 соответственно. Заметим, что новая технология более продуктивна: при любой величине затрат труда она обеспечивает больший выпуск продукта, чем старая (новая кривая расположена выше старой). Обозначим через L$ величину затрат труда, при которой старое и новое значения предельного продукта труда равны между собой. В этой точке касательные к обоим графикам производственных функций параллельны. Как следует из рис. 10.1а, при затратах труда, меньших Lq, новый предельный продукт больше старого (касательная круче). Соответственно новое значение спроса на труд также больше. При затратах труда, превышающих Lq, новое значение предельного продукта труда меньше старого, и спрос на труд также меньше (см. рис. 10.16). Таким образом, при численности персонала, меньшей Lq, внедрение данной технологии приводит к необходимости найма новых работников, а при численности, большей Lq, — к некоторому сокращению численности персонала.

Модель спроса на труд конкурентной фирмы называют также простои моделью спроса на труд.