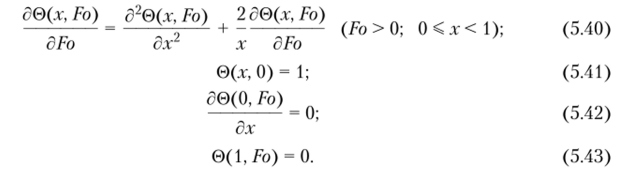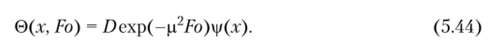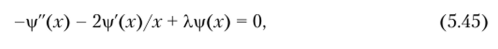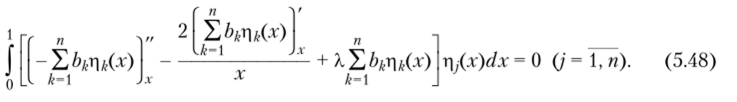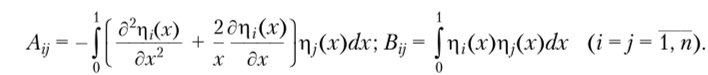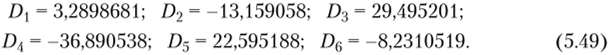Шар (граничные условия первого рода)

В качестве конкретного примера рассмотрим также эффективность совместного применения методов Фурье и Бубнова —Галеркина в решении симметричной задачи теплопроводности для шара при граничных условиях первого рода в следующей математической постановке:

Следуя методу разделения переменных, решение задачи (5.40)—(5.43) разыскивается в виде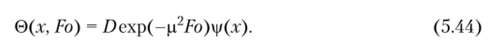

Функция у (х) удовлетворяет уравнению Бесселя вида где X = р².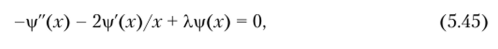

Граничные условия для уравнения (5.45) согласно (5.42), (5.43) будут иметь вид.

Следуя методу Бубнова—Галеркина, решение задачи (5.40)—(5.43) разыскивается в виде (5.37), где г|(х) — координатные функции, определяемые по формуле (5.38).

Для нахождения неизвестных коэффициентов (k = 1, п) составляется невязка уравнения (5.45) и требуется ортогональность невязки ко всем координатным функциям г|ДХ):

Соотношение (5.48) представляет систему однородных алгебраических линейных уравнений вида (5.15), где.

Из системы однородных уравнений находятся собственные числа и коэффициенты /у,. Коэффициенты О/, находятся из начального условия (5.41). Значения этих коэффициентов для шести приближений имеют вид.

На графиках рис. 5.13 представлены результаты расчетов безразмерной температуры по формуле (5.44) в шестом приближении в сравнении с точным решением [49]. Собственные числа для трех и шести приближений, а также точные их значения представлены в табл. 5.4.

Изменения невязки уравнения (5.40) и начального условия (5.41) представлены на рис. 5.14—5.16.

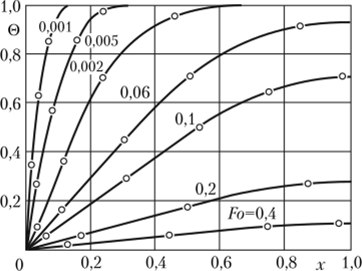
Рис. 5.13. Графики распределения относительной избыточной температуры в шаре:

—расчет по формуле (5.44) (шестое приближение); о — точное решение [49].

Рис. 5.16. Изменение невязки е начального условия при и = 6 (Fo = 0).