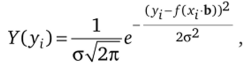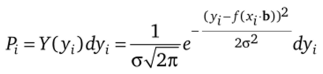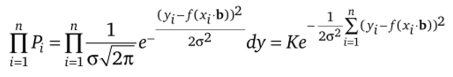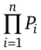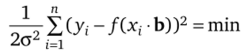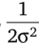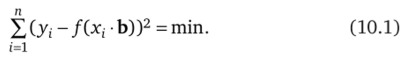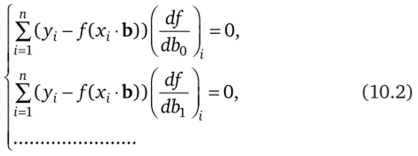Оценка параметров однофакторной регрессионной модели

Оценка параметров однофакторной регрессионной модели методом наименьших квадратов

Для оценки параметров однофакторной регрессионной модели, в случае если функция отклика Y в соответствии со статистическими данными выборки подчиняется нормальному закону распределения, используется метод наименьших квадратов. Поскольку нормальный закон распределения имеет на практике очень широкое распространение, то и метод наименьших квадратов также получил широкое применение для оценки параметров различных однофакторных регрессионных уравнений.

Метод наименьших квадратов основан на так называемом принципе максимального правдоподобия (метод максимального правдоподобия — более общий статистический метод оценивания параметров статистических распределений по отношению к методу наименьших квадратов), суть которого состоит в следующем: необходимо так подобрать математические ожидания распределений/(х; • b) при i = 1, …, п, чтобы вероятность того, что случайные величины Y_x, У₂,…, Y_n приняли совокупность значений у_г, у₂, …,.у_п, была максимальной.

Если условия эксперимента одинаковы для каждого i-ro измерения, то нормальный закон будет иметь вид.

где, а = = а₂= … = а" — среднее квадратичное отклонение. Отсюда соответствующий элемент вероятности будет равен.

Очевидно, что вероятность того, что случайные величины Y_b Y₂ ,…, Y_n примут значения у_ь у₂,…, у_п, равна произведению элементов вероятности р, для всех значений i:

где К — коэффициент, не зависящий от/Ос, • Ь).

Вероятность 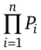будет максимальной, если величина.

откуда, отбрасывая постоянный множитель 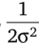?, получаем:

Это и есть требование метода наименьших квадратов — сумма квадратов отклонений экспериментальных точек у, — от уравнения регрессии Да? b) должна обращаться в минимум. Метод наименьших квадратов имеет перед другими методами существенные преимущества:

• • во-первых, он приводит к сравнительно простому способу определения параметров регрессионной модели Ь₀, Ь_ь Ъ₂,…, Ь_п;
• • во-вторых, он имеет довольно веское теоретическое обоснование с вероятностной точки зрения.

Рассмотрим задачу определения параметров Ъ исходя из метода наименьших квадратов. Найдем значения элементов вектора Ь, обращающие левую часть выражения (10.1) в минимум. Для этого продифференцируем ее по элементам вектора b и приравняем производные к нулю:

где 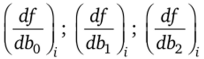 — значения частных производных функции Дх_;? Ь) по параметрам Ъ₀, Ь_ь Ъ₂,… в точке х,.

Система уравнений содержит столько же уравнений, сколько неизвестных Ь₀, Ь_1г Ъ₂,… Решить эту систему в общем виде нельзя, для этого необходимо задаться конкретным видом функции Дат, • Ь).