Задачи о покрывающих деревьях

Пусть задан неориентированный граф G = (X, ?). Дерево D (Y, I) называется покрывающим деревом графа G (X, ?), еслиХ= Yи! с?. Таким образом, покрывающее дерево связывает все вершины данного графа, но необязательно при этом включает все его ребра. На рис. 16.12, а показан граф, для которого на рис. 16.12, б построено покрывающее дерево. Очевидно, что любой связный граф содержит хотя бы одно покрывающее дерево.

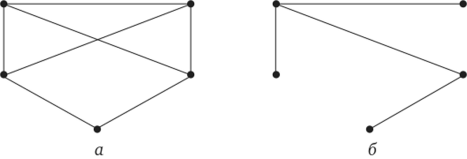
Рис. 16.12. Исходный граф и покрывающее дерево.

Существует ряд стандартных задач, к которым сводятся многие приложения графов.

Задача 1. Для заданной сети S = (G, С) построить покрывающее дерево минимального веса.

К этой задаче могут быть сведены многие практические проблемы. Вот одна из них. В строящемся микрорайоне необходимо разработать схему подводки газа к домам, причем затраты на строительство должны быть наименьшими. На языке теории графов задача будет формулироваться следующим образом: для заданного множества домов построить схему газоснабжения таким образом, чтобы суммарная стоимость строительства была минимальной. Для решения этой задачи удобной моделью является взвешенный граф, вершины которого соответствуют домам, ребра — возможным газовым коммуникациям между ними, веса ребер — стоимости прокладки газопровода между соответствующими домами.

Ниже мы покажем, что при рассмотрении таких задач лучше предварительно решить другую, более простую задачу.

Задача 2. Для связного графа G (X, Е) без петель построить покрывающее дерево.

Идея решения этой задачи следующая. Предварительно строят так называемые связки. Связка представляет собой некоторое поддерево искомого покрывающего дерева. Для построения связки последовательно выделяются отдельные вершины, объединенные некоторыми ребрами. По мере рассмотрения все новых и новых ребер исходного графа связки постепенно нарастают и объединяются, до тех пор пока не будет получена одна единая связка, включающая в себя все вершины графа — искомое покрывающее дерево. При образовании связок следует следить за тем, чтобы не образовывались циклы. Процедуру выделения вершин и ребер во время выполнения алгоритма называют окрашиванием.

Алгоритм построения покрывающего дерева.

Шаг 0. Все ребра исходного графа G (X, Е) не окрашены и множество связок пусто.

Шаг 1. Произвольным образом выбирается ребро. Окрашиваем это ребро. Формируем из этого ребра и инцидентных ему вершин первую связку.

Шаг 2. Произвольным образом выбираем следующее неокрашенное ребро. При этом возможно возникновение одной из четырех ситуаций.

• 2.1. Обе вершины выбранного нового ребра принадлежат выбранной ранее связке (в дальнейшем — одной из рассмотренных ранее связок). Исключаем выбранное ребро из дальнейшего рассмотрения. Переходим к шагу 3.
• 2.2. Одна вершина выбранного ребра принадлежит одной из связок, а другая не принадлежит ни одной из связок. Окрашиваем ребро и включаем его вторую концевую вершину в ту связку, в которую входит первая концевая вершина (наращиваем связку). Переходим к шагу 3.
• 2.3. Ни одна из вершин, инцидентных выбранному ребру, не принадлежит ни одной из связок. Окрашиваем это ребро и формируем новую связку из выбранного ребра и смежных ему вершин. Переходим к шагу 3.
• 2.4. Концевые вершины выбранного ребра принадлежат различным связкам. Окрашиваем это ребро. Обе связки, которые связывает рассматриваемое ребро, сливаем в одну связку и переходим к шагу 3.

Шаг 3. Если все ребра графа рассмотрены, то переходим к шагу 4, иначе переходим к шагу 2.

Шаг 4. Если получилась единственная связка, то она и является искомым покрывающим деревом, иначе задача не имеет решения. Конец алгоритма.

зп.

Примечание 16.1. Описанный алгоритм относится к так называемым поедающим алгоритмам, в которых судьба рассматриваемых элементов решается только один раз на протяжении всей процедуры. Поэтому если число вершин графа конечно, то алгоритм заканчивается за конечное число шагов. Поедающие алгоритмы считаются самыми быстрыми из комбинаторных алгоритмов.

Примечание 16.2. Изложенный алгоритм позволяет построить одно из возможных покрывающих для исходного графа деревьев, поскольку очередное ребро выбирается произвольным образом.

Примечание 16.3. Если алгоритм не заканчивается построением покрывающего дерева, то это означает, что граф G (X, ?) не связный и поставленная задача не имеет решения. Признаком такой ситуации является наличие более чем одной связки при рассмотрении всех ребер графа.

Пример 16.1.

Построить покрывающее дерево для графа, изображенного на рис. 16.13.

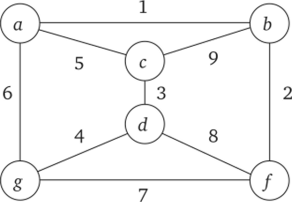
Рис. 16.13. Исходный граф для задачи о покрывающем дереве.

Решение. Произвольным образом пронумеруем ребра графа, например так, как показано на рисунке. Согласно изложенному алгоритму первое выбранное ребро (а, Ь) образует первую связку D_: = {(a, b)}. Второе ребро (b, f) окрашивается (реализуется ситуация 2.2), а связка 6_г уже включает вершины а, b и/ (рис. 16.14, а).

Выбор третьего ребра (с, d) реализует случай 2.3. Поэтому образуется вторая связка D₂ = {(с, d)} (рис. 16.14, б). Четвертое выбранное ребро (d, g), как показано на рис. 16.14, в, наращивает вторую связку: D₂ = {(с, d), (d, g)}.

Рассматривая следующее ребро (а, с), видим, что реализуется шаг 2.4. Это требует объединения обеих связок в одну, а именно D₃ = = {(a, b), (b, f), (a, c), (c, d), (d, g)}. Шестое ребро в дерево не включается, так же как и все остальные ребра. В итоге получаем покрывающее исходный граф дерево (рис. 16.14, г).

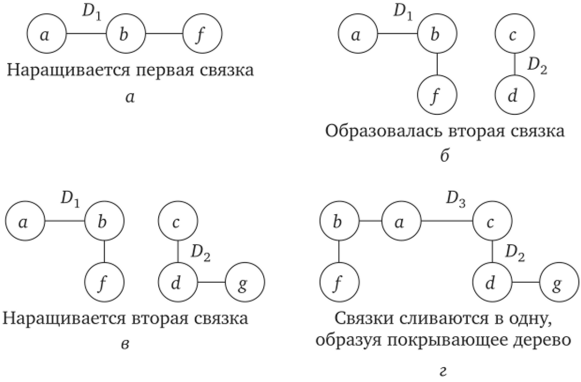
Рис. 16.14. К решению задачи о покрывающем дереве.

Из приведенного выше алгоритма очевидно, что граф в общем случае может иметь более одного покрывающего дерева. Необходимость выбора наиболее подходящего дерева и приводит к задаче 1 — задаче построения покрывающего дерева минимального веса. В таком случае можно поступить следующим образом. В целом сохранить алгоритм решения задачи 2, но выбирать очередное ребро не произвольным образом, а строго в порядке возрастания весов.

Пример 16.2.

Построить минимальное покрывающее дерево для графа, изображенного на рис. 16.15, где цифры при ребрах (в скобках) означают вес соответствующего ребра.

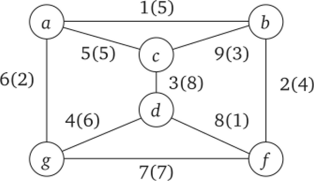
Рис. 16.15. Исходный граф к решению задачи о минимальном покрывающем дереве.

Решение. Первым выбирается ребро (d, f), так как оно имеет наименьший вес, равный единице. Второе ребро (a, g) образует вторую связку {a, g}. Следующим должно быть выбрано ребро (с, Ь), которое образует третью связку {с, Ь}.

Ребро (b, f) объединяет первую и третью связку {d, /, с, b}. Следующим ребром может быть либо ребро (а, Ь), либо (а, с). Пусть это будет ребро (а, с). Тогда необходимо объединить имеющиеся связки в одну {d, f, с, b, a, g}. Все вершины просмотрены и включены в единственную связку, поэтому оставшиеся ребра можно не рассматривать.

В итоге имеем дерево, изображенное на рис. 16.16 и имеющее вес 15. Сравните этот вес с весом дерева изображенного на рис. 16.15, г, вес которого составляет 27.

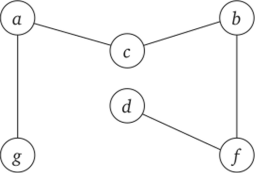
Рис. 16.16. Покрывающее дерево.

Покажем, что описанный алгоритм обеспечивает построение дерева минимального веса, используя метод от противного.

Пусть для исходного графа по алгоритму построили покрывающее дерево веса Q, но для него уже известно покрывающее дерево минимального веса Р. Занумеруем ребра в том порядке, как их выбирали. Чтобы доказать эффективность алгоритма, необходимо показать, что веса графов равны, т. е. L (P) = L (Q).

Если Р и Q не совпадают, то они отличаются хотя бы одним ребром. Пусть такое ребро есть (а, Ь) и М (а, b) — цепь графа с весом Р, идущая из а в Ь.

Если (а, Ъ) добавить к Р, то получится цикл (так как Р — дерево). Но Q не имеет циклов, поэтому в цикле, получившимся в Р, имеется хотя бы одно ребро, не принадлежащее Q. Пусть это ребро веса U. Удалив его из Р, получим граф Р' с тем же числом ребер, что и Р.

Найдем вес графа Р'

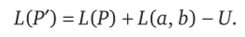
Но по условию граф Р имеет наименьший вес, следовательно, L (P)< U. Но ребро (а, b), когда его выбирали, было ребром наименьшего веса, при добавлении которого к Р не получалось цикла. Поэтому U — L{a, b) и Р', следовательно, имеет вес, равный весу графа Р.

Повторяя эти рассуждения для каждого ребра, получим, что L (Q) = L (P).