Геометрическая интерпретация основной задачи линейного программирования

Рассмотрим особенности задач линейного программирования, используя геометрические построения. Для удобства иллюстрации будем рассматривать тот частный случай, когда число неизвестных ровно на две единицы превышает число линейно независимых уравнений, т. е. п — т = 2. В этом случае возможна иллюстрация рассуждений на плоскости.

Как следует из вышеизложенного, решение системы ограничений (14.6) в этом случае содержит ровно две свободные (независимые) переменные. Какие переменные выбрать в качестве независимых — решает исследователь. Пусть у нас свободными будут переменные Xj и х₂, тогда х₃, х₄,…, х_п станут базисными. Иначе говоря, решение такой системы можно получить в следующем виде:

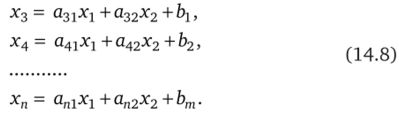
Геометрически каждое уравнение системы (14.8) описывает бесконечную прямую линию в координатах (х_1; х₂). Пересекаясь, каждые две из этих линий образуют так называемые угловые точки. Теоретически возможны случаи, когда угловую точку (при п — т = 2) образуют более двух линий, однако на практике это встречается крайне редко. В общем же случае угловую точку образует не менее (п — т) плоскостей.

Поскольку в ОЗЛП все п переменных должны быть неотрицательными, то с учетом системы (14.8) условия (14.7) можно переписать в следующем виде:

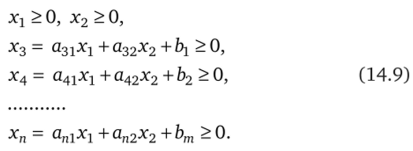
Каждое из условий (14.9) определяет полуплоскость, в которой соответствующая переменная неотрицательна. Совокупность же этих условий может определять некоторую область — область допустимых решений (рис. 14.2). Первые два из этих условий говорят о том, что область допустимых решений задачи линейного программирования может находиться только в положительном квадранте.

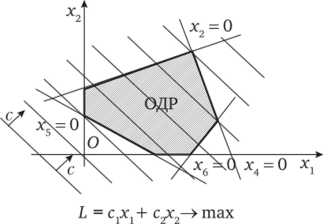
Рис. 14.2. Область допустимых решений.

При разделении переменных на свободные и базисные целевая функция L после подстановки выражений (14.8) в функцию (14.1) также будет выражена только через базисные переменные т. е.

Линия, описываемая этим уравнением, называется линией целевой функции ОЗЛП.

При решении задачи линейного программирования может встретиться один из трех случаев. Область допустимых решений может быть ограниченной (см. рис. 14.2), неограниченной (рис. 14.3) или не иметь ни одного решения (см. рис. 14.1). Последний случай возникает тогда, когда система ограничений (14.6) несовместна.

Рис. 14.3. Случай неограниченной области допустимых решений.

Теорема 14.1. Множество допустимых решений ОЗЛП— выпуклое множество.

Доказательство. Предположим, что ОДР — невыпуклое множество (применяется метод от противного). В этом случае в ОДР найдутся такие две точки, А и В, что на отрезке, их соединяющем, лежит точка С, не принадлежащая ОДР (рис. 14.4). Мы докажем теорему, если при таком предположении придем в дальнейшем к противоречию.

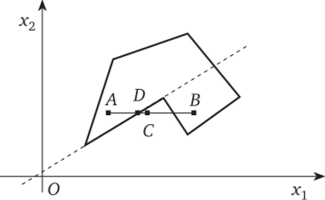
Рис. 14.4. Иллюстрация невозможности невыпуклой ОДР.

Действительно, если точка А принадлежит, а точка С не принадлежит ОДР, то через соединяющий их отрезок обязательно проходит граница области допустимых решений (на рис. 14.4 это точка D). Выше показано, что в задачах линейного программирования (при п — т = 2) границей ОДР является бесконечная прямая (в общем случае — гиперплоскость). Следовательно, все точки отрезка АВ, лежащие по ту же сторону, что и точка С, должны не принадлежать ОДР. Однако это не так. По построению такая точка существует. Это точка В. Мы пришли к противоречию, что и свидетельствует о доказательстве теоремы.

Примечание 14.1. В линейном программировании областей допустимого решения типа представленного на рис. 14.4 не может существовать. Если же в задаче хотя бы одно ограничение нелинейно, то ситуация такого типа возможна (рис. 14.5).

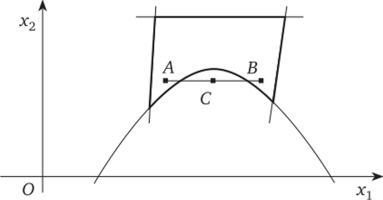
Рис. 14.5. Существование невыпуклой ОДР при нелинейной системе ограничений.

Доказанная теорема позволяет также утверждать, что любой найденный локальный максимум целевой функции является глобальным максимумом, т. е. соответствует решению поставленной задачи.

Если условия (14.6) и (14.7) определяют множество лишь допустимых угловых точек, то условие (14.1) позволяет найти среди них наилучшую (с точки зрения принятого критерия). Уравнение (14.10) — эквивалент (14.1) — задает в пространстве свободных переменных (х_1; х₂) некоторую прямую, которая при изменении этих переменных перемещается параллельно сама себе (см. рис. 14.2). Известно, что градиент показывает направление наискорейшего возрастания функции. В рассматриваемой задаче градиент целевой функции (gradL) есть вектор С = (у_х, у₂). Очевидно, что по комбинации знаков коэффициентов и у₂ (всего четыре варианта) можно определить направление, в котором вектор С возрастает. Для примера, иллюстрируемого рис. 14.2, его увеличение направлено вверх направо.

Чем дальше перемещать линию целевой функции по направлению вектора С, тем с точки зрения принятого критерия (наибольшего значения L) лучше. Однако лучшее решение должно быть одновременно и допустимым, т. е. удовлетворять всем ограничениям задачи: и (14.6), и (14.7). Геометрически это означает, что линия целевой функции должна иметь с ОДР хотя бы одну общую точку. Поскольку в линейном программировании ОДР есть выпуклый многогранник, то такая точка (решение задачи!) обязательно есть одна из его вершин. Напомним, что каждая из вершин многогранника является угловой точкой, т. е. там пересекается не менее (п — т) прямых (в общем случае гиперплоскостей).

Становится ясным, что решение ОЗЛП можно найти, перебирая только вершины ОДР. Та из вершин, где значение целевой функции наибольшее, является решением задачи.

Поскольку каждая из вершин есть точка пересечения (п — т) гиперплоскостей, на каждой из которых соответствующая неизвестная равна нулю, то в решении не менее (п — т) переменных обращается в нуль. Иначе говоря, структура решения задачи линейного программирования всегда имеет вид.

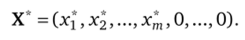
Примечание 14.2. Если в направлении возрастания целевой функции ОДР не имеет границ, соответствующая ОЗЛП имеет решение в бесконечной точке (см. рис. 14.3). На практике это означает отсутствие реально достижимого решения.

Изложенные соображения иногда позволяют найти решение ОЗЛП, используя так называемый геометрический метод.

Пример 14.3.

Найти максимум целевой функции при условиях.

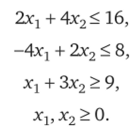
Решение. Решение данной задачи проведем исходя из геометрических соображений. Если заменить заданные неравенства на точные равенства.

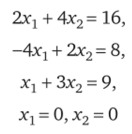
и построить соответствующие прямые (рис. 14.6), то областью допустимых решений будет треугольник АВС. Вектор, показывающий направление увеличения целевой функции L, есть вектор (1, 1). Следовательно, наиболее удаленной является точка С, которая образована пересечением линий 1 и 3.

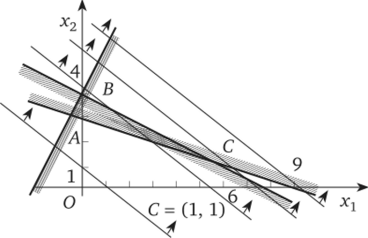
Рис. 14.6. Геометрическая интерпретация ОЗЛП.

Это означает, что решение задачи есть решение системы уравнений.

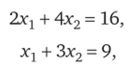
т.е. решением задачи является точка X = с, в которой целевая функция достигает своего наибольшего значения V = 6+1 = 7.