Задачи.
Сфера и шар
Так как они прямоугольные, MF — общий катет, — по условию. Таким образом, FA=FC=FB=FD, точка F равноудалена от вершин основания, то есть является центром описанной около основания окружности. Нарисуем сечение пирамиды и шара плоскостью AMC. Точка O — центр шара,. По теореме синусов в: Цистерна имеет форму цилиндра, к основаниям которой присоединены равные шаровые сегменты. Радиус цилиндра равен… Читать ещё >
Задачи. Сфера и шар (реферат, курсовая, диплом, контрольная)
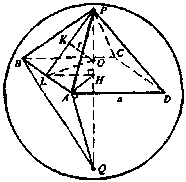
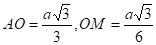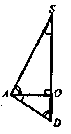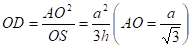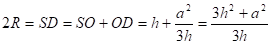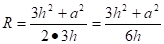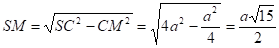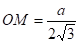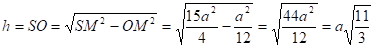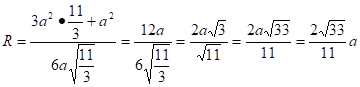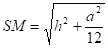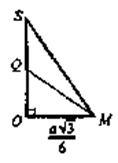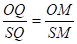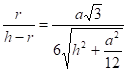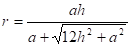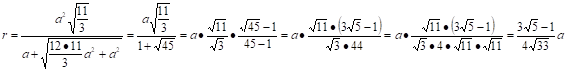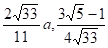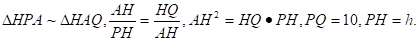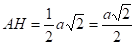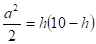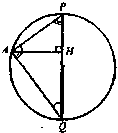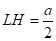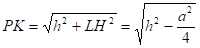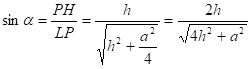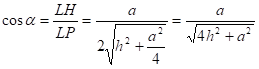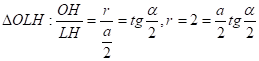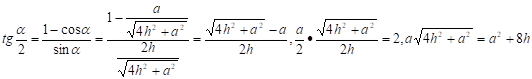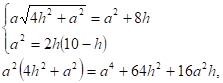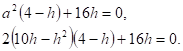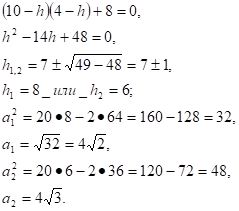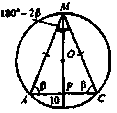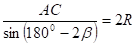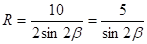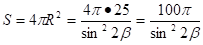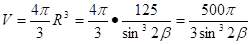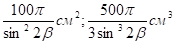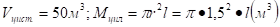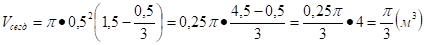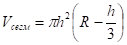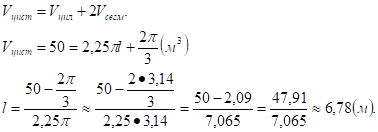Задачи на поверхности
Задача № 1.
В правильной треугольной пирамиде сторона основания равна a, а боковое ребро равно 2a. Найдите радиусы вписанной и описанной сфер.
Решение:
SO — высота пирамиды; SO=h.
Пусть O — центр основания пирамиды, M — середина BC, AM — высота в .
.
Центры обеих сфер лежат на прямой SO, SO плоскости ABC. Найдём R — радиус описанной сферы. Продолжим SO до пересечения с описанной сферой в точке D. SD — диаметр шара,. Из подобия треугольников и :
.
.
.
Проведём отрезок SM.
Из .
поэтому из :
Найдём радиус r вписанной сферы.
Пусть Q — центр вписанного шара, тогда в QM — биссектриса .
.
По свойству биссектрисы внутреннего угла треугольника:
.
.
Ответ: .
Задача № 2.
В правильной четырёхугольной пирамиде радиусы вписанной и описанной сфер равны 2 см и 5 см.
Найдите сторону основания и высоту пирамиды.
Решение:
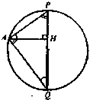
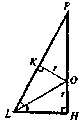
Продолжим высоту пирамиды PH до пересечения со сферой в точке Q. PQ — диаметр, центр описанной сферы лежит на высоте PH, или на её продолжении за точку H. Соединим отрезком точку A с точкой H. Рассмотрим сечение плоскостью APQ.
как опирающийся на диаметр,.
Пусть a — сторона основания, тогда .
Тогда .
Проведём, отрезок PL., плоскость плоскости. Пусть O — центр вписанной сферы, — биссектриса .
.
Пусть .
;
.
Из .
Решим систему:
Разделим обе части на .
Ответ: см; 8 см или 6 см, см.
Задачи на объёмы тел
Задача № 3
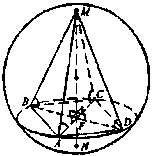
В шар вписана пирамида, основанием которой является прямоугольник с диагональю 10 см. Какое боковое ребро составляет с основанием угол. Найдите площадь поверхности и объём шара.
Решение:
Проведём высоту пирамиды MF; проведём отрезки.
FA, FB, FC, FD.
так как они прямоугольные, MF — общий катет, — по условию. Таким образом, FA=FC=FB=FD, точка F равноудалена от вершин основания, то есть является центром описанной около основания окружности. Нарисуем сечение пирамиды и шара плоскостью AMC. Точка O — центр шара,. По теореме синусов в :
.
где R — радиус шара.
.
Площадь поверхности шара:
(см2).
Объём шара:
(см3).
Ответ: .
Задача № 4
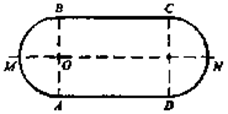
Цистерна имеет форму цилиндра, к основаниям которой присоединены равные шаровые сегменты. Радиус цилиндра равен 1,5 м, а высота сегмента равна 0,5 м. Какой длины должна быть образующая цилиндра, чтобы вместимость цистерны равнялась 50 м3?
Дано:. .
— шаровые сегменты.
Решение:
.
где.
Ответ: м.