Определение доли рынка (иллюстрация метода Маркова)

Рассмотрим варианты приобретения двух различных марок, А и Б. Предположим, что существует определенная последовательность, а именно: АБАБ, АББА, ББАА, ААББ. Каждая последовательность предполагает две покупки марки, А и две покупки марки Б. Таким образом, вероятность совершения покупки (или степени лояльности) для марки, А составляет 50% в случае, если воздействие на нее последовательности совершения покупок не учитывается. Аналогично и для марки Б. При условии, что покупка определенной марки ведет к изменению последующих поступков потребителя, вероятность приобретения марки, А при каждой пятой покупке должна отличаться при различных вариантах последовательностей. Справедливо предположить, что вероятность совершения покупки, А — р (А) будет выше при наблюдении последовательности ББАА, нежели после последовательности ААББ, несмотря на то, что в каждой последовательности обе марки приобретаются одинаковое число раз.

В случаях, когда опыт прошлых закупок относится к числу значимых факторов, лояльность к определенной марке должна меняться в результате текущего покупательского поведения. 50% лояльность к торговой марке должна увеличиваться или уменьшаться в зависимости от того, какую последовательность совершения покупок выказал потребитель.

Один из самых распространенных методов решения вышеуказанной задачи является метод Маркова, описывающий вероятностный подход к описанию явлений, которые дискретно развиваются во времени. Время рассматривается не как некоторая непрерывная величина, а как дискретные периоды. В основе теории марковских процессов лежит гипотеза о зависимости результата п + 1 испытания от результатов всех предшествующих испытаний через результат п — того (предыдущего) испытания. Итак, марковские случайные процессы — это процессы с дискретными состояниями и непрерывным временем. Процесс называется с дискретным состоянием, если все его возможные состояния можно заранее перечислить, т. е. состояние системы принадлежит к конечному множеству N = {n,}. Процесс с непрерывным временем — это если смена состояний может произойти в любой случайный момент, при этом считается, сто переход системы из одного состояния в другое происходит мгновенно.

Предположим, что существуют две марки определенного товара X и У. В среднем потребитель приобретает товар данного типа примерно раз за период времени (день, неделя, месяц, квартал и т. д.). После проведенных исследований на лояльность потребителей марке исследователь имеет данные:

• 1. Из каждых 10 пользователей марки X в среднем шесть человек предполагают приобретать ее и в следующий раз.
• 2. Из каждых десяти пользователей марки У в среднем семь с половиной человек предполагают приобретать ее и в следующий раз.

Таким образом, мы имеем дело с вероятностью перехода от одной марки к другой. По собранным данным можно построить матрицу одноступенчатых переходов Z. Она будет иметь следующий вид:

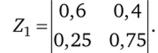
Верхняя строка матрицы показывает состояние перехода по марке X, нижняя — по марке У, причем, сумма по строке всегда будет равняться 1 или 100%. Смысл модели, подложенной Марковым, заключается в том, что существует некоторая тенденция переходов системы из одного состояния в другое. Необходимо определить соответствующие вероятности переходов. Процедура поиска этих вероятностей в упрощенном варианте (т.е. без приведения соответствующей доказательной математической базы^[1]) имеет следующую логику.

1. Построение матрицы двухступенчатого перехода. Вероятность того, что потребитель, пользующийся маркой X, будет продолжать ее использовать и в следующий период равна сумме вероятностных переходов от X—>Х (по нашим данным 6 человек из 10, или р_х_>_х = 0,6) и от У—>Х (по нашим данным 2,5 человека из 10, р_у_,_х=0,25). В общем для марки X имеем:

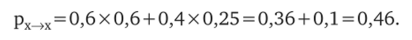
Графически это можно представить следующим образом (см. рис. 6.3).

Аналогично рассчитываются вероятности перехода от X—>У, от У—>У и от У—>Х:

Рх^_у = 0,6×0,4 + 0,4×0,75 = 0,24 + 0,3 = 0,54 Р_у_>_у= 0,4×0,25 + + 0,75×0,75 = 0,1+ 0,5625 = 0,6625 р_у_,_х = 0,25×0,6 + 0,75×0,25 = = 0,15 + 0,1875 = 0,3375.

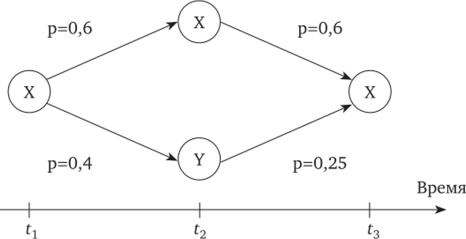
Рис. 6.3. Процесс двухступенчатого перехода.

В результате получаем матрицу двухступенчатых переходов:

2. Если мы продолжим рассмотрение, то можно определить вероятности на следующий период времени, т. е. построить матрицу трехступенчатых переходов. Построение будет производиться исходя из выявленной в процессе опроса лояльности марке (предположим, что она сохраниться, особенно если мы имеем «консервативное» население и если уровень жизни населения определенного региона невысокий). Графически этот процесс для переходов от X—>Х изображен рис. 6.4.

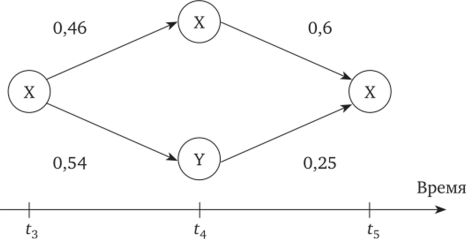
Рис. 6.4. Процесс последующего (трехступенчатого) перехода.

Остальные вероятностные состояния можно определить аналогичным образом:

р_х->у = 0,46хО, 4 + 0,54×0,75 = 0,184 + 0,405 = 0,589 Р_у_, у = 0,3375х х 0,4 + 0,6625×0,75 = 0,135 + 0,4969 = 0,6319;

р_ун>х=0,3375×0,6 + 0,6625 X 0,25 = 0,2025 + 0,1656 = 0,3681.

Матрица Z₃, так же как и матрица Z₂, может быть рассчитана с помощью матричной алгебры, а именно:

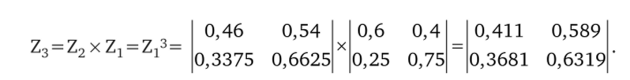
В общем случае для к-той ступени перехода соответствующая матрица может быть рассчитана по следующей формуле:

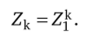
В итоге получаем вероятности переключения клиента с марки X на марку У в различные периоды времени.

Вышеуказанный принцип можно использовать для определения доли рынка определенной марки. Обозначим объем реализации на рынке в определенное время как q. Тогда, если принять, что существует марка товара X и все остальные марки, можно выразить это состояние как:

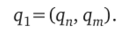
где q_n + q_m=q_i=100%, q_n — доля рынка для марки X, q_m — для рынка всех остальных марок.

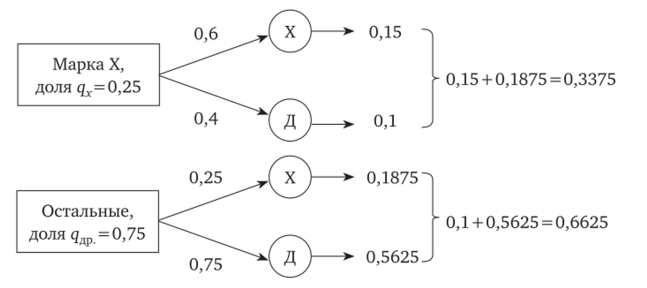
Рис. 6.5. Расчет прогнозных долей рынка.

Это значит, что весь объем реализации на рынке можно представить как сумму двух долей — марки X и всех остальных марок данного товара. Предположим, что марка X занимает ¼ всего рынка, а все остальные марки ¾. Тогда можно выразить существующее состояние на первый период времени как:

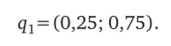
Определим, какую долю рынка будет контролировать марка X на следующем этапе, т. е. в следующий период (см. рис. 6.5).

Итак, исходя из наших расчетов можно написать состояние рынка в период два:

В результате все расчеты могут быть выражены в следующем общем виде: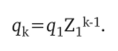

Для более четкого выявления тенденции можно использовать теорему теории массового обслуживания, которая носит название первой эргодической теоремы. Данная теорема доказывает, что, если исходная матрица Z_x не имеет нулевых элементов, то:

1. Существует единственный вектор q, для которого.

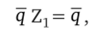
где q — является неподвижным вектором для Z_v

• 2. По мере роста к матрица Z_a^k приближается к матрице Z, в которой каждая строка совпадает с q.
• 3. Для каждого исходного вектора q^ увеличением к вектор приближается к q.

На основе этой теоремы сразу по исходным данным матрицы Z может быть рассчитан вектор q . В общем виде задача может быть записана следующем виде:

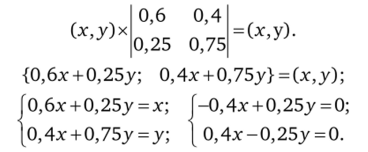
Если принять во внимание, что в общем виде х + у =1, то можно решить любую систему:

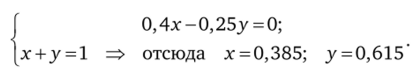
Этот результат означает, что независимо от нынешнего состояния рынка, если матрица переходов Zj останется неизменной, то будет наблюдаться тенденция к тому, что марка X будет контролировать 38,5% рынка, а все остальные 61,5% рынка.

Получение данных для построения модели Маркова связаны с проведением специальных исследований, основой которых будет выявление лояльности марке. В качестве метода исследования могут быть использованы различные варианты опросов или эксперимент, целью которых является выяснение степени удовлетворенности определенной маркой и намерение (или отказ) что-либо поменять.

Допустим, рынок определенного товара представлен тремя марками А, В и С. Исследователю известно, что на текущий момент времени марка, А имеет 40% рынка, марка В — 30% и марка С — 30% рынка. Для того, чтобы спрогнозировать доли этих трех марок на будущий период, исследователь провел эксперимент, результаты которого показали следующее (см. табл. 6.5).

Таблица 6.5

Матрица переключений потребительских предпочтений

Результаты исследования показали: вероятность того, что купившие марку, А сейчас купят ее снова в следующем периоде, составляет 70%, вероятность переключения на марку В — 20%, а на марку С — 10%. Марку В, вероятно, предпочтут купить в следующем периоде 40%, 50% переключаться на марку, А и 10% — на марку С. Вероятность сохранения предпочтения к марке С у купивших ее в первый период составит всего лишь 20%, на марку А, вероятно, переключатся 60%, а на марку В — 20%. Исходя из этого исследователь может определить долю марки А, В, и С на последующий период.

Рыночная доля марки А: 40×0,7 + 30×0,5 + 30×0,6 = 61%.

Рыночная доля марки В: 40×0,2 + 30×0,4 + 30×0,2 = 26%.

Рыночная доля марки С: 40×0,1 + 30×0,1 + 30×0,2 = 13%.

Подобный эксперимент имеет еще и некоторый побочный результат — выяснилось, что марка, А является наиболее удачной (имеет более приемлемое для клиента соотношение цена/качество), по сравнению с маркой В и С. При проведении эксперимента можно определить причину такого положения, сразу определив направления улучшения марки В и марки С. Если данные собирались методом опроса, то для выявлении причины сложившегося положения, а именно, почти полная неудовлетворенность маркой С и менее значительная неудовлетворенность маркой В, необходимо организовывать и проводить дополнительные исследования.

В общем, маркетинг может извлечь некоторые основные принципы деятельности из этой модели. В конечном итоге можно попытаться оказать воздействие на вероятность переключения на другую марку, т. е. разработать комплекс маркетинговых мероприятий по изменению лояльности потребителей.

Метод экстраполяции использует исторические данные по ряду интересующих показателей. Это один из наиболее широко используемых методов прогнозирования в фирмах — построение тренда изменения величины. Привлекательность его состоит с том, что можно опираться только на достоверные внутренние данные, в то же время опасность применения только этого метода в невозможность учесть момент перелома ситуации. Применение метода экстраполяции данных предполагает, что выполняется ряд условий:

• • имеются в наличие данные за длительный период наблюдения — более 10—12 периодов;
• • периоды, в которые собираются данные, должны иметь схожие характеристики (условия среды примерно одинаковы);
• • если периоды наблюдения не соответствуют требованиям схожести, то применение метода экстраполяции становится рискованным, и тогда лучше перейти к экспертным методам анализа ситуации.

Наиболее популярные методы экстраполяции основываются на экспоненциальном сглаживании, которое реализует принцип: «Наиболее свежая информация обладает большим весом». Используется для краткосрочного прогноза и основаны на средневзвешенном значении продаж по определенному числу периодов.

Эконометрические методы используют информацию для прогноза параметров при различных ограничениях. Всегда существует проблема — что можно использовать из предшествующего исследования? Примером применения данного метода может быть расчет кривой спроса. Оценки в данном случае отношений могут модифицироваться на базе экспертной информации и данных временных рядов. И здесь снова необходима надежная информация. Эконометрические методы позволяют эффективно соединить теоретические (экспертные) и статистические источники. Эконометрические методы наиболее применимы, когда:

• 1) существуют явные причинные взаимосвязи;
• 2) эти связи описаны количественными параметрами;
• 3) при прогнозах надо иметь в виду перемены в причинных связях (например, могут произойти изменения в потребительских предпочтениях) ;
• 4) эти изменения могут быть спрогнозированы или проконтролированы.

Если любое из этих условий не выполняется, что типично для прогнозирования с малым «горизонтом», то эконометрические методы не дадут достоверного результата.

Эконометрика в маркетинге представлена методами линейного моделирования, а также динамического программирования, моделями, базирующимися на теории массового обслуживания и теории принятия решений, имитационными моделями. В силу сложностей среды маркетинговой деятельности применение данных методов весьма ограничено.

• [1] Доказательную базу см.: Дубров А. М. и др. Многомерные статистические методы: учебник. — М.: Финансы и статистика, 1998.