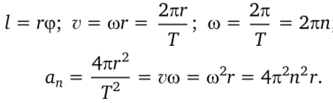Механика. 
Физика

Механика — раздел физики, изучающий механическое движение тел.

Механическое движение — изменение взаимного расположения тел или их частей в пространстве с течением времени.

Кинематика

Кинематика — раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — модель тела, размерами которого в данных условиях движения можно пренебречь. Масса тела сосредоточена в этой точке.

Тело отсчета — произвольно выбранное тело, относительно которого определяется положение других (движущихся) тел.

Система координат — совокупность (в простейшем случае прямоугольная декартова система) трех взаимно перпендикулярных числовых осей х, у, z с общим началом координат, связанным с телом отсчета.

Система отсчета — тело отсчета, связанная с ним система координат и выбранный способ измерения времени.

Положение точки А в декартовой системе координат определяется тремя координатами х, у, z, а также радиусом-вектором г (рис. 2.1).

Траектория — линия, вдоль которой движется тело в данной системе отсчета.

Путь AS — скалярная величина, равная длине участка траектории между начальным и конечным положениями тела.

Вектор перемещения (или перемещение) Дг — вектор Аг = г2 — г_ъ проведенный из начальной точки пути в конечную.

Рис. 2.1.

Скорость — векторная величина, характеризующая направление и быстроту движения. Единица скорости: метр в секунду (м/с).

Средняя скорость — векторная величина, равная отношению перемещения АР к промежутку времени At, в течение которого это перемещение произошло:

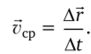
Модуль вектора средней скорости:

Следует различать среднюю скорость прохождения пути и модуль вектора средней скорости.

Средняя скорость прохождения пути:

где Л S' — путь, пройденный телом за время At'; AS_1; A S₂, …, AS_n — части пройденного пути со скоростями п_ь v₂, …, v_n за интервалы времени At_a, At₂,…, At_n соответственно.

Средняя скорость, очевидно, тем лучше характеризует движение, чем меньше At, и поэтому заставим At стремиться к нулю (At —? 0).

Мгновенная скорость — это скорость тела в данный момент времени (в данной точке траектории):

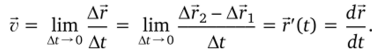
Модуль мгновенной скорости:

Направление вектора средней скорости Р_ср совпадает с направлением вектора перемещения Дг, а вектор v направлен по касательной к траектории в сторону движения (рис. 2.2).

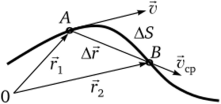
Рис. 2.2.

Равномерное движение — движение, при котором материальная точка за любые равные промежутки времени совершает равные перемещения.

Скорость равномерного движения материальной точки:

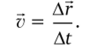
Вектор скорости v совпадает по направлению с вектором перемещения, А г.

Равномерное прямолинейное движение — движение с постоянной по модулю и направлению скоростью:

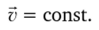
В этом случае | Дг| = S и v = т'_ср = const, а = 0.

При равномерном прямолинейном движении путь:

Кинематическое уравнение равномерного движения материальной точки вдоль оси х:

где л:₀ — координата тела в начальный момент времени; v_x — проекция вектора скорости v на ось x;t — время движения тела.

Знаки «плюс» или «минус» перед слагаемыми определяются при выборе начальной координаты х₀ и проецировании вектора д на ось координат.

На графике зависимости пути S от времени (рис. 2.3, а) и координаты х от времени (рис. 2.3, б) скорость численно равна тангенсу угла наклона графика:

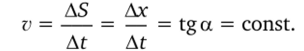
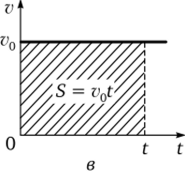
По графику зависимости скорости v от времени t можно определить путь, пройденный телом, как площадь фигуры, ограниченной графиком и осью времени (рис. 2.3, в).

Рис. 2.3.

Принцип суперпозиции (наложения): скорость результирующего движения (в данный момент времени) есть векторная сумма скоростей составляющих движений (рис. 2.4, а):

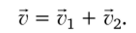
Классический закон сложения скоростей: скорость тела в неподвижной системе отсчета равна векторной сумме скорости подвижной системы отсчета и скорости этого тела относительно подвижной системы (рис. 2.4, б):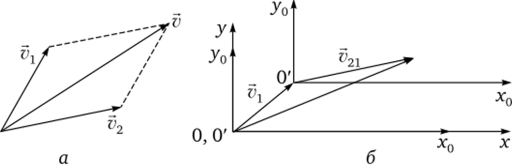

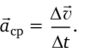
Рис. 2.4.

Здесь v — вектор скорости относительно неподвижной системы отсчета; д — вектор скорости подвижной системы; г₂₁ — вектор скорости тела относительно подвижной системы отсчета.

Ускорение — векторная величина, характеризующая быстроту изменения скорости по величине и направлению. Единица измерения — метр на секунду в квадрате (м/с²).

Среднее ускорение — векторная величина, численно равная отношению изменения скорости Ад к промежутку времени At, за которое это изменение произошло:

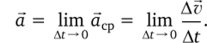
Мгновенное ускорение — векторная величина, равная пределу отношения изменения скорости к промежутку времени At, когда последнее неограниченно стремится к нулю:

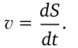
Для любого движения модуль мгновенной скорости равен первой производной пути во времени:

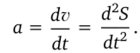
Мгновенное ускорение — первая производная скорости по времени и вторая производная пути по времени:

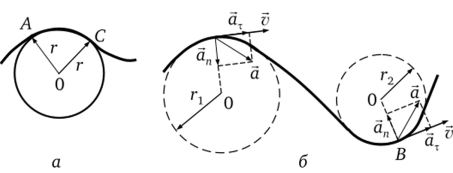
При достаточно малом времени At длина дуги траектории АС будет достаточно малой и ее можно считать дугой окружности (рис. 2.5, а). Ее центр 0 называется центром кривизны, а радиус г — радиусом кривизны в данной точке траектории.

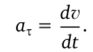
Puc. 2.5.

Составляющие ускорения:

• тангенциальная — характеризует быстроту изменения скорости по модулю (рис. 2.5, б; направлена по касательной к траектории):

• нормальная — характеризует быстроту изменения скорости по направлению (рис. 2.5, б; направлена к центру кривизны траектории):

Полное ускорение при криволинейном движении:

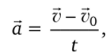
Равнопеременное прямолинейное движение — движение, при котором скорость материальной точки за любые равные промежутки времени изменяется на равные величины.

Ускорение равнопеременного движения:

где б₀ — начальная скорость (в момент времени t₀ = 0); б₀ — скорость в произвольный момент времени f.

Равнопеременное прямолинейное движение — движение с постоянным по модулю и направлению ускорением:

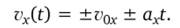
Равнопеременное движение может быть равноускоренным (движение с положительным ускорением) и равнозамедленным (движение с отрицательным ускорением).

Проекция вектора скорости, например, на ось х:

Путь S при переменном прямолинейном движении:

Уравнение координаты х при равнопеременном прямолинейном движении имеет вид:

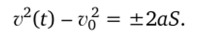
где х₀ — начальная координата тела в момент времени t = 0; а_х — проекция ускорения а на ось Ох.

Знаки «±» определяются при выборе начальной координаты х₀при проецировании векторов v и а на ось х.

Соотношение между квадратами конечной и начальной скорости тела, ускорением и пройденным путем:

Средняя скорость равнопеременного движения:

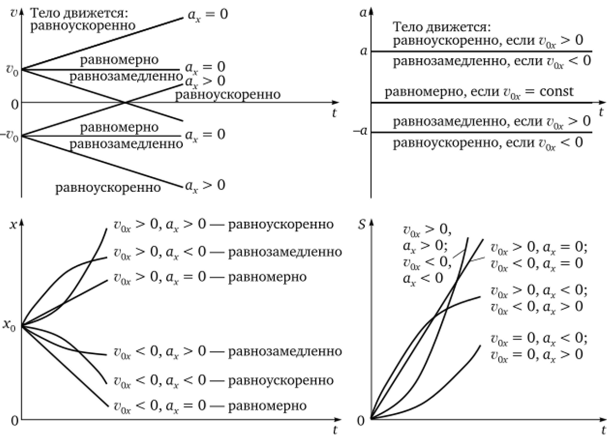
Графики зависимости скорости, ускорения, координаты тела, пути от времени приведены на рис. 2.6.

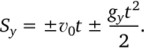
Рис. 2.6.

Свободное падение — движение тела в безвоздушном пространстве под действием силы тяжести. Ускорение, с которым движется тело при свободном падении, называется ускорением свободного падения (а = g направлено к центру Земли, g = 9,81 м/с² ~ 10 м/с²). Как любой вектор, ускорение свободного падения g может быть разложено на составляющие g_x и g_y вдоль координатных осей: g — g_x + g_y.

Путь тела:

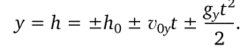
Координата тела (или его высота):

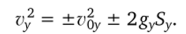
Скорость тела в любой точке пути:

Скорость тела в любой момент времени:

Знаки «+» или «-» определяются при выборе начальной координаты h₀ (при t = 0) и проекциями соответствующих векторов д, а и g на ось у.

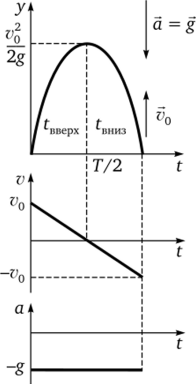
Графики координаты у, скорости v и ускорения а тела, брошенного вертикально вверх с поверхности Земли №₀ = 0), показаны на рис. 2.7.

Рис. 2.7.

Движение тела, брошенного под углом к горизонту. Тело брошено под углом а к горизонту с начальной скоростью v₀ (рис. 2.8). Изучаемое движение складывается из равномерного горизонтального движения со скоростью v_0x и движения тела, брошенного вертикально вверх со скоростью и_0х.

Рис. 2.8.

Проекция вектора начальной скорости на ось Ох: 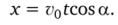Координата х тела:

Проекция начальной скорости на 0у:

Координата у тела и проекция его скорости v_y на ось Оу соответственно:

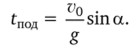
Время движения до верхней точки траектории:

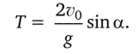
Время движения (полета): Максимальная высота подъема:

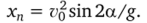
Дальность полета:

Равномерное движение материальной точки по окружности — движение, при котором точка (тело) за равные промежутки времени проходит равные по длине дуги окружности.

При равномерном движении по окружности модуль скорости тела постоянен (т. е. v = const), но направление вектора скорости изменяется и, следовательно, это движение происходит с ускорением (рис. 2.9).

Следует заметить, что всякое криволинейное движение, даже равномерное, есть движение с ускорением.

Рис. 2.9.

Угловая скорость:

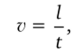
где ф — угол поворота радиус-вектора от начального положения; t — время, за которое произошел этот поворот.

Единица угловой скорости: радиан в секунду (рад/с). Линейная скорость:

где / — длина дуги окружности АВ (рис. 2.9, а), пройденной точкой за время t.

Единица линейной скорости: метр в секунду (м/с).

Период вращения (Г) — время одного полного оборота по окружности. Если за время t совершается N оборотов, то период вращения:

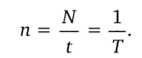
Единица периода вращения: секунда ©.

Частота вращения (п) — число полных оборотов в единицу времени:

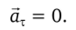
Единица частоты: секунда в минус первой степени (с^-1 = 1/с). Тангенциальная составляющая ускорения при равномерном движении точки по окружности равна нулю:

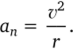
Нормальная составляющая ускорения (центростремительное ускорение):

Единица тангенциальной и нормальной составляющей ускорения: метр на секунду в квадрате (м/с²).

Ускорение материальной точки при равномерном движении по окружности является центростремительным. В любой точке окружности вектор центростремительного ускорения направлен к центру окружности и перпендикулярен вектору скорости (рис. 2.9, б).

Связь между линейными и угловыми величинами при равномерном движении точки по окружности: