Третий закон Ньютона

Действие тел друг на друга носит характер взаимодействия.

Третий закон Ньютона отражает тот факт, что сила есть результат взаимодействия тел, и устанавливает, что силы, с которыми действуют друг на друга два тела, равны по величине и противоположны по направлению:

Например, сила давления тела на опору F,_|an:i и сила реакции опоры N (приложенные к разным телам) по третьему закону Ньютона связаны соотношениями: Р_даш1 = -N; = N.

Однако третий закон справедлив нс всегда. Он выполняется в случае контактных взаимодействий, т. е. при соприкосновении тел, а также при взаимодействии тел, находящихся на расстоянии друг от друга, но покоящихся друг относительно друга.

Мы уже отмечали, что законы Ньютона плохо работают при и * с (релятивистская механика), а также при движении тел очень малых размеров, сравнимых с размерами элементарных частиц.

Уравнение движения системы материальных точек. Теорема о движении центра масс

В любой системе частиц имеется одна замечательная точка С, называемая центром инерции, или центром масс, которая обладает рядом интересных и важных свойств. Положение этой точки характеризует распределение масс этой системы.

Радиус-вектор простой системы двух частиц (рис. 3.1) массами т и т₂

, _В /и. г, -г т₇%

можно наити, но формуле г_с = ——-—.

т_х + т₂

В общем случае (рис. 3.2) радиус-вектор центра масс системы, состоящей из п материальных точек, равен:

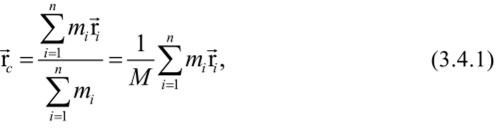
п где т = - общая масса системы, п — число материальных точек системы.

При этом не надо путать центр масс с центром тяжести системы — с точкой приложения равнодействующей сил тяжести всех тел системы.

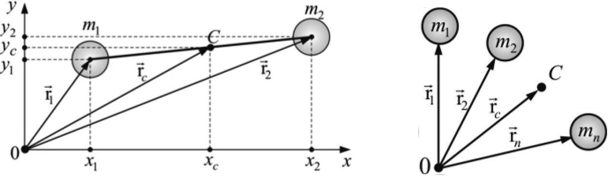
Рис. 3.1. В В В Рис. 3.2.

Центр тяжести совпадает с центром масс (центром инерции), если g (ускорение силы тяжести) для всех тел системы одинаково (когда размеры системы гораздо меньше размеров Земли).

Рассмотрим систему, состоящую из п взаимодействующих между собой материальных точек (или тел, принимаемых в условиях данной задачи за материальные точки), обладающих соответственно: массами: т^, т_г,…, т_п…т_п

скоростями: б, б₂,…, б₁.,…о_и;

импульсами: р, р₂р, ,".р".

Вектор полного импульса механической системы, равен геометрической сумме импульсов отдельных материальных точек (или частиц) системы:

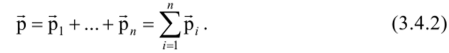
Движение каждой частицы определяется уравнением (в соответствии со // законом Ньютона (3.2.2)).

П _.

где: F_;'^wyrp' - 'У F, _t — результирующая всех внутренних сил, действую;

it^.

ы

щих на данную /-ю частицу; F_ik — сила, действующая на /-ю частицу со.

/ w Г’ВНСШ.

стороны к-и частицы; г, — результирующая внешних сил, приложенных к j-й частице системы со стороны частиц (тел), нс входящих в состав рассматриваемой механической системы.

Используя (3.4.2) и (3.4.3), получим уравнение движения системы материальных точек (частиц).

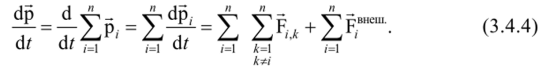
Так как для любой внутренней силы всегда существует парная ей сила, равная по величине и противоположно направленная, согласно третьего закона Ньютона, т. е. F_i Jt = -F_{A (}. (например, F₁₂ = -F,), то результирующая всех внутренних сил системы частиц равна нулю: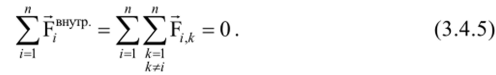

Введем обозначение.

Здесь г — результирующая всех внешних сил, приложенных к системе материальных точек.

Подставив (3.4.5) и (3.4.6) в (3.4.4), получаем уравнение движения системы материальных точек

Каждая материальная точка системы имеет свою скорость, свое ускорение, однако в нерелятивистском случае уравнению (3.4.7) можно дать определенное толкование, используя понятие о центре масс.

В однородном поле сил тяжести центр инерции совпадает с центром тяжести системы. Воспользуемся величиной F (3.4.1) и преобразуем выражение для импульса системы частиц.

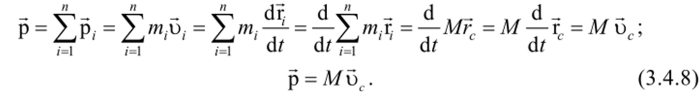
Подставив (3.4.8) в (3.4.7) получим уравнение движения центра масс системы частиц.

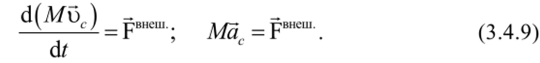
В твердом теле центр масс занимает постоянное положение относительно других точек тела, поэтому данные уравнения полностью описывают поступательное движение твердого тела.

Теорема о движении центра масс:

Центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, под действием силы, равной геометрической сумме всех внешних сил, действующих на систему.