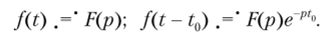Другие работы

Которые позволяют использовать их во многих случаях взамен бронз и баббитов. Сплавы на цинковой основе (ЦАМ 9−1,5, ЦАМ 10−5) характеризуются низкой температурой плавления (~ 400° С), в большей степени, чем у бронз и алюминиевых сплавов, размягчением при нагревании и, таким образом, хорошей прирабатываемостью. Благодаря эффекту снижения абразивной активности свободных абразивных частиц путем…
Реферат 
Способность электрического аппарата (или любой электроустановки) противостоять действию электромагнитных сил, возникающих при протекании токов короткого замыкания, называют электродинамической стойкостью. Если вектор 12 тока в элементе dl2 лежит в плоскости, образованной проводником 1 и точкой 2, как на рис. 6.1, б, то вектор индукции В12 перпендикулярен вектору тока 12. Поэтому в выражении (6.2…
Реферат 
Где Акn, Arяа, Arав, Arhc — объёмные активности Rn и его дочерние продукты распада 2,8Ро (RaA), 2,4Pb (RaB), 2,4Bi (RaC) Бк/м3, соответственно; Fru — коэффициент равновесия, который определяется как отношение эквивалентной равновесной объемной активности радона в воздухе к реальной объемной активности Rn, т. е. величина Frh характеризует степень сдвига равновесия между Rn и продуктами его распада.
Реферат 
К этим процессорам относятся МП фирмы Intel 8080, 8086/8088 и 80 286. Первым МП, на основе которого стали создавать персональные компьютеры, был МП 8080. Он был 8-разрядным, имел тактовую частоту 2 МГц и содержал 6 тыс. транзисторов. Производительность такого компьютера была невысокой, однако ее оказалось достаточно для успешного применения в качестве контроллера различных приборов, устройств…
Реферат 
При t > 7р* разрушенной областью в поперечном сечении трубы является кольцо, внутренний и наружный радиусы которого г* и г2 (рис. 6.28), и фронт разрушения, представляющий собой поверхность кругового цилиндра радиуса г*, будет двигаться к внутренней поверхности трубы. Уравнение движения фронта может быть получено из соотношения (6.33). Для этого вместо сттах следует подставить окружное напряжение…
Реферат 
Рис. 1. Приемы выполнения разделки конца кабеля: а — резка конца кабеля ножницами НС, б — наложение бандажа из просмоленной ленты, в — наложение прополочного бандажа, г — надрезание брони, д, е, ж — удаление брони, кабельной пряжи подушки и защитной кабельной бумага на оболочке, з — разметка, и, к — круговые надрезы свинцовых оболочек, л, м, н, о — продольные надрезы алюминиевой, свинцовой…
Реферат 
Сверлением получают сквозные и глухие отверстия. Рассверливанием увеличивают диаметр ранее просверленного отверстия. Зснкерованием увеличивают диаметр отверстия, ранее полученного в заготовке литьем или давлением. Развертывание — чистовая операция, обеспечивающая высокую точность отверстия. Развертыванием обрабатывают цилиндрические и конические отверстия после зенкерования или растачивания…
Реферат 
А. Поле внутри проводящего тела в условиях электростатики. Если тело не заряжено, то, естественно, суммарный заряд тела равен нулю. Поскольку тело помещено в поле, то вследствие явления электростатической индукции в нем произойдет разделение зарядов. В результате этого разделения на поверхности тела, обращенной в сторону более высокого потенциала (рис. 2.2), выступят отрицательные заряды…
Реферат 
Помещения, где проводятся работы на стационарных установках с закрытыми радионуклидными источниками излучения, должны быть оборудованы системами блокировки и сигнализации о положении источника (блока источников). Кроме того, должно бьггь предусмотрено устройство для принудительного дистанционного перемещения источника излучения в положение хранения в случае отключения энергопитания установки или…
Реферат 
Стенку можно рассматривать как неподвижный шар с и2 = 0> массой ш2 —" со. Разделим числитель и знаменатель на т2 и пренебрежем /и, / т2, тогда. В данном случае можно воспользоваться законом сохранения механической энергии и законом сохранения импульса (в проекциях на ось х): Рис. 6.7. Система Зелия — шарик, Рис. 6.8. Полная кинетическая и скользящий без трения по проволоке потенциальная энергии…
Реферат 
Капельное орошение — самый экономичный способ увлажнения, при котором вода подается прямо в корнеобитаемый слой небольшими дозами, через специальные водовыпускные отверстия (капельницы), устанавливаемые через каждые 50… 100 см на увлажняющих трубопроводах. Управление системой капельного орошения должно обеспечить нужную последовательность увлажнения отдельных участков и коррекцию нормы полива…
Реферат 
Определим параметры схемы замещения (рис. 5.4,6) Л0, х0,20, а также значения тока 1х=1а и его реактивную и активную составляющие 1]р и /1а, на основании опытных данных. Если пренебречь /?, и х, (так как Я"Яо и Х1"хо, т. е. приняв Л, = 0, х, = 0), то мощность, потребляемая от сети: Тогда В опыте холостого хода измеряются напряжения на входе и выходе трансформатора с помощью вольтметров РУ] и РУ2…
Реферат 
Рабочую АРД-диаграмму строят для конкретных параметров контроля: материала изделия, частоты упругих колебаний, радиуса преобразователя, угла ввода луча. В качестве основного сигнала Ад можно использовать эхосигнал от бокового цилиндрического отражателя или отражение от бесконечной плоскости (донного сигнала). В действующей нормативно-технической документации АРДдиаграммы приводятся в виде таблиц…
Реферат 
Щепетов, А. Г. Теория, расчет и проектирование измерительных устройств. В 3 ч. Ч. 1. Теория измерительных устройств / А. Г. Щепетов. — М.: Стандартинформ, 2006. Шехонин, А. А. Методология проектирования оптических приборов: учеб, пособие / А. А. Шехонин, В. М. Домненко, О. А. Гаврилина. — СПб.: Изд-во СПбГУИТМО, 2006. Васильев, В. П. Основы теории и расчета цифровых фильтров: учеб, пособие для…
Реферат 
В радиотехнических системах сегодня широко используются интегральные операционные усилители (ИУ) со специальными элементами обратной связи, формирующими амплитудно-частотную характеристику (АЧХ) резонансного типа. Однако классическое построение таких ИУ сопровождается значительными энергетическими потерями, которые идут в основном на обеспечение статического режима достаточно большого числа…
Реферат