Граничные условия. 
Электродинамика и распространение радиоволн

Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с различными электрическими свойствами.

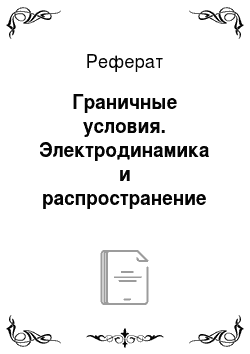
А. Поле внутри проводящего тела в условиях электростатики. Если тело не заряжено, то, естественно, суммарный заряд тела равен нулю. Поскольку тело помещено в поле, то вследствие явления электростатической индукции в нем произойдет разделение зарядов. В результате этого разделения на поверхности тела, обращенной в сторону более высокого потенциала (рис. 2.2), выступят отрицательные заряды и на противоположной стороне — положительные заряды. Хотя сумма зарядов тела и будет равна нулю, но заряды, выступившие на поверхности тела, окажут существенное влияние на поле вне проводящего тела и на поле внутри проводящего тела. В области вне тела, особенно вблизи него, поле может существенно исказиться по сравнению с тем полем, которое было, если бы проводящее тело в поле отсутствовало.

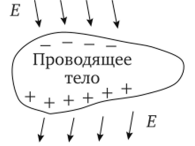
Рис. 2.2. Проводник в электростатическом поле.

Все точки проводящего тела в условиях электростатики имеют один и тот же потенциал. В этом можно убедиться исходя из противного. Если допустить, что в условиях электростатики между двумя точками проводящего тела может быть разность потенциалов, то тогда под действием этой разности потенциалов электроны в теле начали бы перемещаться. Упорядоченное движение зарядов в теле противоречило бы самому определению электростатического поля как поля, созданного неподвижными зарядами (в макроскопическом смысле слова).

Поскольку все точки проводящего тела имеют один и тот же потенциал, то между двумя любыми бесконечно близко расположенными друг к другу точками приращение потенциала равно нулю, следовательно, и Е = -—п тоже равно нулю. Физически напряженность поля дп

внутри проводящего тела равна нулю (в макроскопическом смысле слова), потому что напряженность от внешнего поля компенсируется равной ей по значению и противоположной по знаку напряженностью от зарядов, расположившихся на поверхности тела.

Если тело будет заряжено, то все принесенные извне на тело заряды и заряды, разделившиеся в теле вследствие явления электростатической индукции, также расположатся на поверхности тела таким образом, что потенциал всех точек будет один и тот же, а напряженность внутри тела будет равна нулю.

Б. Условия на границе раздела проводящего тела и диэлектрика.

На границе «проводящее тело — диэлектрик» всегда выполняются два условия:

1) отсутствует тангенциальная (касательная к поверхности) составляющая напряженности поля:

2) вектор электрического смещения D в любой точке диэлектрика, непосредственно примыкающей к поверхности проводящего тела, численно равен плотности заряда X на поверхности проводящего тела в этой точке, т. е.

Рассмотрим первое условие. Все точки поверхности проводящего тела имеют один и тот же потенциал. Следовательно, между двумя любыми очень близко расположенными друг к другу точками поверхности приращение потенциала dtp = 0, но dcp= E_tdl, следовательно, E_tdl = 0.

Поскольку элемент пути dl между точками на поверхности не равен нулю, то равны нулю Е_г

Для доказательства второго условия мысленно выделим бесконечно малый параллелепипед (рис. 2.3). Верхняя грань его параллельна поверхности проводящего тела и расположена в диэлектрике. Нижняя грань находится в проводящем теле. Высоту параллелепипеда возьмем очень малой (сплющим его). Применим к параллелепипеду теорему Гаусса. Из-за малости линейных размеров можно принять, что плотность заряда X на поверхности ds проводящего тела, попавшей внутрь параллелепипеда, одна и та же. Полный заряд внутри рассматриваемого объема равен Ids.

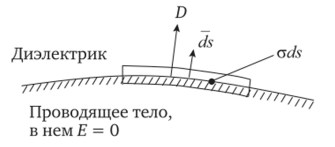
Рис. 2.3. Граничные условия.

Поток вектора D через верхнюю грань объема равен Dds =Dds. Поток вектора D через боковые грани объема отсутствует из-за того, что вектор D перпендикулярен к ним. Через «дно» объема поток также отсутствует, так как внутри проводящего тела Е = 0и?> = 0(е проводящего тела есть величина конечная). Таким образом, поток вектора D из объема.

В. Условия на границе раздела двух диэлектриков с различными электрическими проницаемостями. На границе раздела двух диэлектриков выполняются два следующих условия:

1) равны тангенциальные составляющие напряженности поля:

2) равны нормальные составляющие электрической индукции:

Индекс «1» относится к первому диэлектрику, индекс «2» — ко второму.

Первое условие вытекает из того, что в потенциальном полej>Edl =0 по любому замкнутому контуру. Второе условие представляет собой следствие теоремы Гаусса. Покажем справедливость первого условия. С этой целью выделим плоский замкнутый контур mnpqm (рис. 2.4) и составим вдоль него циркуляцию вектора напряженности электрического поля. Верхняя сторона контура расположена в диэлектрике с электрической проницаемостью е₂, нижняя — в диэлектрике с? j. Длину стороны тп, равную длине стороны pq, обозначим dl. Контур возьмем так, что размеры пр и qm бесконечно малы по сравнению с dl. Поэтому составляющими интеграла ф Ed I вдоль вертикальных сторон из-за их малости пренебрежем.

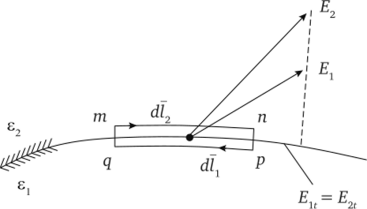
Рис. 2.4. Плоский замкнутый контур mnpqm.

Составляющая j>Edl на пути тп равна E₂dl₂ =E_2tdl, на пути pq —.

EidTi=—Ei_tdl.

Знак «минус» появляется как следствие того, что элемент длины на пути pq и касательная составляющая вектора Ej направлены в противоположные стороны (cosl80° =-1).

Таким образом, j> Edl = E_2tdl — E_udl = 0, или E_xt = E₂t.

Убедимся в справедливости второго условия. С этой целью на границе раздела двух сред выделим параллелепипед очень малых размеров (рис. 2.5). Внутри выделенного объема есть связанные заряды и нет свободных (случай наличия свободных зарядов на границе раздела рассмотрим отдельно), поэтому.

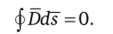
Поток вектора D через верхнюю грань площадью ds равен D₂ds2=D₂nds. Поток вектора через нижнюю грань Djdsj ~-D_uds; |ds]| = |ds₂| = ds.

Рис. 2.5. Малый параллелепипед на границе двух сред.

Следовательно, j>Dds = -D_lnds + D_2nds = 0, или Dpi = D₂n.

При наличии на границе раздела двух сред свободных зарядов с плотностью? (это встречается очень редко).

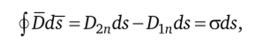
т.е. при этом.

Таким образом, при наличии на границе раздела двух сред свободных зарядов нормальная составляющая вектора D скачком изменяется на величину плотности этих зарядов.

Потенциал есть функция непрерывная, поэтому на границе раздела двух сред потенциал не претерпевает скачков.