Теорема Козлова об аффинной эквивалентности изображений

Два изображения называем аффинно эквивалентными (а-экви— валентными), если они переводимы друг в друга аффинными преобразованиями.

Лемма 1. Если два изображения а-эквивалентны, то они эквивалентны.

Доказательство. Нужно показать, в сущности, что при аффинных преобразованиях численные значения элементов их множества Т кода изображения не меняются. Каждый элемент в Т определяется отношением площадей некоторых треугольников. При преобразованиях сдвига, поворота и симметрии эти площади не меняются, а значит не меняется и их отношение. Пусть теперь происходит сжатие (или растяжение) изображения по осям х и у с коэффициентами к_х и к_у. Известно [22], что в этом случае площадь S' фигуры (или любой ес части) будет после преобразования равна Sk_xk_y (здесь S — площадь фигуры до преобразования). Отсюда следует, что если p'_nuvip<7 — соответствующий p_muv, ipq элемент множества множества Т после Преобразования, ТО S_muvk_xky/Sipqk_xky = S_mtiV/Slpq ⁼ Pmuv, lpq•.

Лемма доказана. ?

Пусть изображение В состоит из точек, являющихся подмножеством точек изображения А с кодом < Ма, Та >. Обозначим через Мв множество номеров тех и только тех точек из Л, которые входят в изображение В. Соответственно через Тв обозначим множество всех тех элементов p^f_muvipq из Та, для которых m, u, v, l, p, q € Мв- Изображение В с кодом.

< Мв, Тв > назовем частью изображения А. Любое изображение В'_f a-эквивалентное изображению В, назовем подизображением изображения Л.

Будем называть изображение из четырех точек четырехточечником. Пусть в четырехточечнике Л из точек a, b, с, d точки а, 6 и с расположены на одной прямой. Тогда S_ab_c = 0 и те элементы из Та, для которых в соответствующем отношении S_abc входит в знаменатель, не определены, а те, для которых 5'_6с входит в числитель (при не равном нулю знаменателе), равны нулю. Очевидно, можно утверждать обратное: если код.

< Ма, Та > обладает указанными свойствами, то в четырехточечнике Л точки а, Ь и с расположены на одной прямой. В изображении Л общего вида точки а, 6, с, входящие в изображение, расположены на одной прямой в том и только в том случае, если для любой части изображения Л, являющейся чстырехточечником и включающей точки а, 6, с, выполняется указанное свойство, определяющее расположенность точек а, 6, с на одной прямой. В изображении Л точки а, …, а_п(тх > 3) расположены на одной прямой в том и только в том случае, когда любые три точки из а_ь …, а_п расположены на одной прямой.

Изображение назовем плоским, если все его точки не лежат на одной или двух параллельных прямых.

Лемма 2. Если по коду плоского изображения выбраны какиелибо три его точки, не лежащие на одной прямой, и задано произвольное (но не на одной прямой) положение этих точек

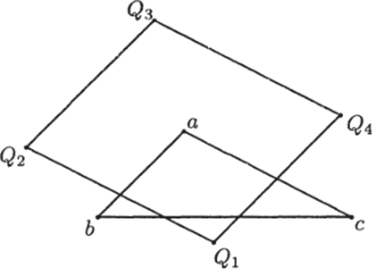
Рис. 1.3:

на плоскости, то положение остальных точек изображения определяется по коду однозначно.

Доказательство. Пусть наш код < Ма, Та > является кодом некоторого плоского изображения А. Пусть га, р, q — три выбранные точки, не лежащие на одной прямой, и а', 6', d их исходное положение. Пусть s — четвертая точка изображения, которая вместе точками га, р, q образует плоское изображение, т. е. если д! — исходное положение точки s, то точки а', 6', d и д! не лежат на одной или двух параллельных прямых.

Предположим, что задано новое положение а, 6, с точек га, р, q. Для определения нового положения точки s воспользуемся процедурой (стандартной) построения по коду четырехточечника четвертой точки при известных положениях остальных трех. Полагаем, что точки а, 6, с разные, лежат не на одной прямой, в остальном же их положение можно задавать произвольным образом. Точку, положение которой определяется, обозначим через х.

Поскольку площадь треугольника abc известна, то, используя S_abx/S_ab_Cl S_aCxf &abci ^bcx/^abo наХОДИМ ПЛОЩаДИ *Sa6x> &acxi Sbcx• Для треугольника abc длины его сторон известны, поэтому можно определить длины высот h_ab, h_ac, hb_c, опущенных из точки х на стороны соответственно ab, ас и 6с. (Одна из этих высот может оказаться нулевой по длине, две быть нулевыми, очевидно, не могут). Таким образом, задача сводится к тому, чтобы по заданному треугольнику abc построить точку х та ;

кую, что высоты из этой точки на стороны ab_f ас и Ьс треугольника есть соответственно h_ab, h_ac и /i&_c. Проводим две прямые, параллельные стороне ab по разные стороны и отстоящие от нее на величину h_аь, и две прямые, параллельные стороне ас по разные ее стороны и отстоящие от нее на величину h_ac. Возникает параллелограмм, вершины которого обозначены на рис. 4 как ??1,(?2><�Эз и Q₄. По построению, точка х может располагаться только на вершинах этого параллелограмма. Для окончательного определения положения точки х нужно провести две прямые, параллельные оставшейся стороне треугольника abc (стороне Ьс на рис. 1.3) и отстоящие от нее на величину hbc- Пересечение этих прямых с вершинами параллелограмма даст возможные положения точки х.

Покажем, что одно такое пересечение гарантированно существует.

Рассмотрим аффинное преобразование, которое переводит точки а', ?', d в точки а, 6 и с. Пусть это аффинное преобразование переводит точку d! в точку d. Согласно лемме 1 это аффинное преобразование не меняет кода и, значит, что точка d является гарантированно существующим положением, точки х. Отметим, что так как аффинное преобразование переводит параллельные прямые в параллельные, то точки а, 6, с и d не лежат на одной или двух параллельных прямых.

Остается вопрос, единственным ли может получиться положение восстанавливаемой точки.

Предположим, что для точки х возможны два разных положения х¹ и х", одно их которых гарантированная точка d.

• 1. Предположим, что точки х' и х" совпадают с Q и Q-z, которые поэтому должны быть равноудалены от стороны Ьс. Следовательно, отрезок Ьс должен делить отрезок Q1Q2 пополам, то есть точка Ь должна лежать на отрезке Q1Q2• В этом случае а, 6, с, х' и х" расположены на двух параллельных отрезках: отрезке ас и отрезке QQ2, и, значит, на двух параллельных отрезках лежат точки а, 6, с и d — пришли к противоречию.
• 2. Аналогичным образом приходим к противоречию в предположении, что х' и х" совпадают с Qi и Q₄.

Если х' и х" совпадают с Q и Q3, то отрезок QQ$ должен делиться стороной Ьс пополам. Однако серединой диагонали Q1Q3 должен делиться стороной 6с пополам. Однако серединой диагонали Q1Q3 параллелограмма является, по построению, точка а.

Если х' и х" совпадают с Q₂ и Q3, то отрезок Q2Q3 должен быть либо параллелен отрезку 6с, либо делиться этим отрезком или его продолжением пополам. И то, и другое противоречиво по построению. Аналогичное имеет место и при совпадении х' и х" с Q₄.

3. Пусть, наконец, х' и х" совпадают с Q₂ и Q₄. Тогда диагональ Q2Q4 должна быть параллельной стороне 6с, что противоречит тому, что точки а, 6, cud не лежат на двух параллельных прямых.

Тем самым мы доказали, что положение точки х определяется однозначно и совпадает с точкой d при условии, что точки то, р, q и s не лежат на двух параллельных прямых.

Разобьем множество точек изображения А, отличных от точек то, р, <7, на два класса А и А₂. В множество А включим точки s такие, что-то, р, <7 и s не лежат на двух параллельных прямых, а класс А₂ составят оставшиеся точки.

Как мы показали выше, положение каждой точки их А определяется однозначно положением точек то, р, q, причем так как изображение А плоское, то множество А — непустое.

Рассмотрим произвольную точку s из множества А₂. Возьмем произвольную точку г из множества А> положение которой уже определено. Точки m, р, q, s и г образуют плоское изображение, значит из четырех m, р, q и г можно выбрать три, что они вместе с точкой s образуют плоское изображение, т. е. не лежат на двух параллельных прямых. Тогда по этим трем точка положение точки s определяется однозначно.

Лемма доказана. ?

Теорема 1. Два плоских изображения эквивалентны точно тогда, когда они а-эквивалентны.

Доказательство. В одну сторону теорема 1 следует из леммы.

1.

Покажем теперь, что если плоские изображения А и В эквивалентны, то они a-эквивалентны. Выберем на А три точки а, 6, с, не лежащие на одной прямой. Пусть следующей из определения эквивалентности биекцией точкам а, 6, с сопоставляются точки соответственно ahd изображения В. Аффинным преобразованием изображения В совместим его точки а', Ь', с' с точками соответственно а, Ь, с изображения Л. Поскольку положение остальных точек изображения В, при заданных точках ad определяется, согласно лемме 2, однозначно, то, следовательно, они совпадут с точками изображения Л.

Теорема доказана. ?