Расчет параметров рабочего режима

Параметрами асинхронной машины называют активные и индуктивные сопротивления обмоток статора и ротора, а также сопротивление взаимной индуктивности и расчетное сопротивление r12 или r, введением которого учитывается влияние потерь в стали статора на характеристики двигателя. Схема замещения фазы обмотки приведенной асинхронной машины показана на рисунке 7.1.

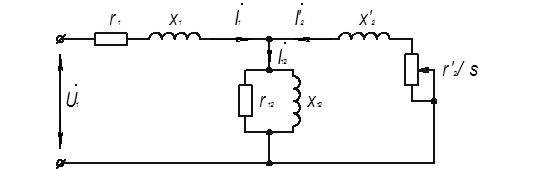
Рисунок 7.1 Т-образная схема замещения фазы приведенной асинхронной машины.

Активное сопротивление фазы обмотки статора r1 определяется по формуле (9.132).

(7.1).

статор проводник зазор машина где 115 — удельное сопротивление материала обмотки при расчетной температуре для класса изоляции F, равной 115, для меди 115=10−6/41Ом м, что равно 2,439 Ом м;

L1 — общая длина эффективных проводников фазы обмотки, вычисляется по формуле (9.134).

(7.2).

где lср — средняя длина витка обмотки.

Для расчета средней длины витка необходимо определить длину пазовой и лобовых частей витка. Длина пазовой части равна конструктивной длине сердечника машины, lп равна 201,5 мм.

Средняя ширина катушки bкт обмотки статора, рассчитывается по формуле (9.147).

;

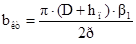
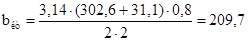
(мм).

Длина лобовой части витка lл определятся по формуле (9.145).

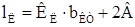
(7.3).

где Кл — коэффициент, значение которого выбирается из таблицы 9.23 при условии, что лобовые части не изолированы, Кл = 1,3;

В — вылет прямолинейной части катушек из паза, В = 10 мм.

По (7.3) получим.

мм.

Средняя длина витка обмотки lср находится по формуле (9.135).

;

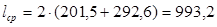
мм.

Общая длина эффективных проводников фазы обмотки по (7.2) равна м.

Активное сопротивление фазы обмотки статора r1 по (7.1) равно.

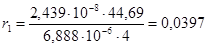
Ом.

Длина вылета лобовой части обмотки lвыл определяется по формуле (9.146).

.

где Квыл — коэффициент, выбранный из таблицы 9.23 Квыл = 0,4;

мм.

Значение сопротивления обмотки статора в относительных единицах находим по формуле (9.186).

;

.

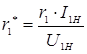
Активное сопротивление фазы обмотки ротора r2 определяется для короткозамкнутых роторов по формуле (9.168).

.

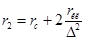
где rс — сопротивление стержня, определяемое по формуле (9.169).

.

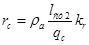
где kr — коэффициент увеличения активного сопротивления от действия эффекта вытеснения тока, в пределах изменения скольжения от холостого хода до номинального режима принимают kr = 1;

а — удельное сопротивление литой алюминиевой обмотки при расчетной температуре, принимаем, а = 0,049 10−6 Ом м;

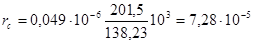
Ом;

rкл — активное сопротивление короткозамыкающих колец, вычисляемое по формуле (9.170).

;

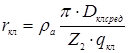
Ом;

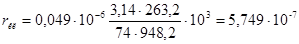
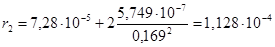
Ом.

Активное сопротивление фазы короткозамкнутой обмотки ротора, приведенное к обмотке статора, определяется по формуле (9.173).

;

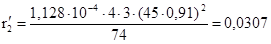
Ом.

Приведенное активное сопротивление фазы короткозамкнутого ротора в относительных единицах вычисляется по формуле.

;

.

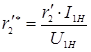
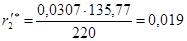
Индуктивное сопротивление фазы обмотки статора x1 определяется по формуле (9.174).

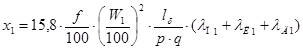
(9.4).

где f — частота питающей сети, f = 50 Гц;

п1 — коэффициент магнитной проводимости пазового рассеяния;

л1 — коэффициент магнитной проводимости лобового рассеяния;

д1 — коэффициент магнитной проводимости дифференциального рассеяния.

Коэффициент магнитной проводимости пазового рассеяния П1 определяется по формуле приведенной в таблице 9.26 для рисунка 9.50 в, г, з.

.

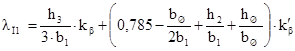
где h3 — высота проводников с учетом изоляции между ними, вычисляется по формуле.

h3 = hп — 2 bиз — hш - b½.

h3 = 31,3 - 2 0,4 - 1 — 9,3/2 = 24,5 мм;

h2 - высота занимаемая пазовым клином; т. к. проводники закрыты пазовой крышкой, то h2 = 0;

k' - коэффициент укорочения, зависящий от шага и определяемый по формуле (9.156).

;

;

k — коэффициент, зависящий от шага обмотки и определяемый по формуле (9.158).

;

;

.

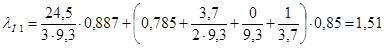
Коэффициент магнитной проводимости лобового рассеяния Л1 определяется по формуле (9.159).

;

.

Коэффициент магнитной проводимости дифференциального рассеяния Д1 определяется по формуле (9.160).

.

где 1 — коэффициент, зависящий от числа пазов на полюс и фазу q = 5, укорочения шага обмотки 1 = 0,8, размерных соотношений зубцовых зон и воздушного зазора = 0,8 мм, определяется по формуле (9.176).

.

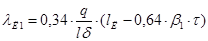
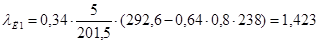
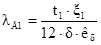
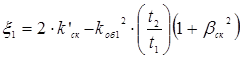
где ск — коэффициент скоса пазов, ск = 0;

к’ск — коэффициент, определяемый по рисунку 9.51, д, к’ск = 0,8;

;

.

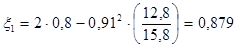
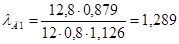
По (9.4) получим.

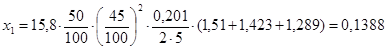
Ом.

Значение индуктивного сопротивления обмотки статора в относительных единицах определяется по формуле.

;

.

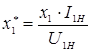
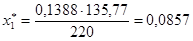
Индуктивное сопротивление фазы обмотки ротора х2 вычисляется по формуле (9.177).

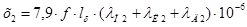
(9.5).

где п2 — коэффициент магнитной проводимости пазового рассеяния стержня ротора;

л2 — коэффициент магнитной проводимости лобового рассеяния стержня ротора;

д2 — коэффициент магнитной проводимости дифференциального рассеяния стержня ротора.

Коэффициент магнитной проводимости пазового рассеяния п2 определяется по формуле приведенной в таблице 9.27 для рисунка 9.52, а.

.

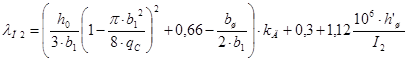
где kд — коэффициент, принимаемый в номинальном режиме равным единице;

h0 — высота паза, принимаемая равной 27,3 мм;

.

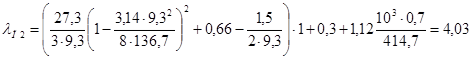
Коэффициент магнитной проводимости лобового рассеяния л2 определяется по формуле (9.178).

.

Коэффициент магнитной проводимости дифференциального рассеяния д2 определяется по формуле (9.180).

.

где 2 — коэффициент, рассчитываемый по формуле (9.181).

.

где z — коэффициент, определяемый по рисунку 9.51, а, z = 0;

;

.

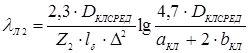
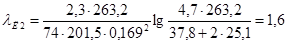
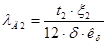
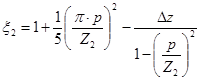
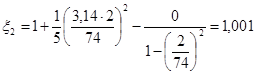
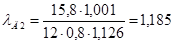
Тогда по (9.5) получим.

(Ом).

Приведенное к обмотке статора индуктивное сопротивление рассеяния фазы ротора определяется по формуле (9.183).

;

.

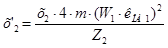
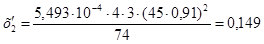
Приведенное индуктивное сопротивление фазы короткозамкнутого ротора в относительных единицах вычисляется по формуле.

;

.
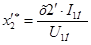