Проверка адекватности регрессионной модели

Использование регрессионных моделей для решения практических задач возможно лишь в случае, если они отражают существенные связи. Поэтому так важна проверка адекватности таких моделей, цель которой выяснить, не являются ли параметры полученного уравнения регрессии результатом действия случайных причин.

Значимость параметров парной линейной регрессии применительно к совокупностям объемом не больше 30 проверяют с помощью /-критерия Стьюдента. Для достаточно больших совокупностей используют таблицу интеграла вероятностей нормального закона распределения.

Фактические (расчетные) значения /.-кри терия для а_{) и а_л определяются по следующим формулам:

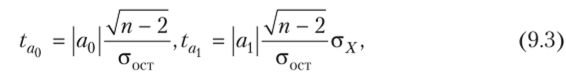
* 1т-Ц)²

где п — объем совокупности: а_ост = . —— --—среднее квадратическое.

V п

отклонение фактических значений результативного признака от его рас- 132.

/К*/-*)2 Ixx? (IX,)2.

четных значении; а. = А——¹-или, а = J-— - ——- — среднее.

V п ' у п { п)

квадратическое отклонение фактических значений факторного признака от его среднего уровня.

Рассчитанные по формулам (9.3) значения t сравниваются с критическим значением t, определяемым, но таблице Стыодента с учетом уровня значимости¹ а и числом степеней свободы² v.

В социально-экономических исследованиях, а обычно пронимают равным 0,05. Параметр признается значимым, если ?_расч > ?_табл. В этом случае отклоняется гипотеза о том, что значения а₀ и а_х обусловлены только случайными причинами и связь между X и У не носит закономерного характера.

Пример 9.2.

Рассмотрим продолжение примера 9.1. Проверим значимость параметров уравнения.

Расчетные величины, используемые при оценке адекватности регрессионной модели.

• 1 Уровню значимости соответствует вероятность, с которой может быть опровергнута та или иная гипотеза. Уровню значимости 0,05 (5%) и 0,01 (1%) соответствуют вероятности 0,95 и 0,99.
• 2 Число степеней свободы о = п — (k + 1), где к — число факторных признаков в уравнении.

Для расчета ст_()ст используем данные графы 7, полученные как разность граф 3 и 7 из таблицы примера 9.1:

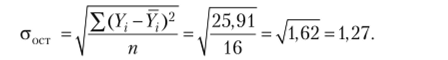
Расчет о у выполним по данным в графах 2 и 4:

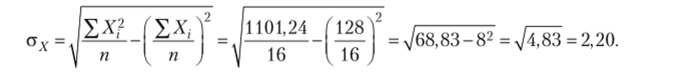
Расчетные значения 1-критерия Стыодента:

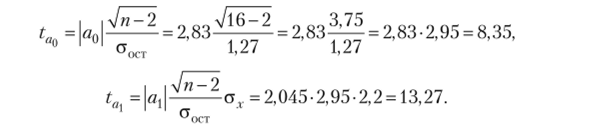
Уровню значимости, а = 0,05 при v = 14(16−2) соответствует критическое значение f-критсрия: ?_{та6 |}= 2,145.

Таким образом, расчетные значения t_ag незначительно превосходят табличное значение 1-критерия. Это означает, что оба параметра уравнения значимы и связь между заработной платой и выработкой рабочих в исследуемой совокупности не случайна.^[1][2]

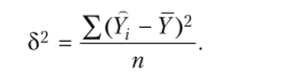
В результате формула (9.4) принимает вид.

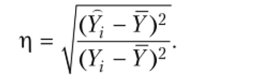
Теоретическое корреляционное отношение применяется для измерения тесноты связи между результативным и факторным признаками при линейной и криволинейной корреляционной зависимости. Значение его может находиться в пределах от нуля до единицы, т. е. О < r| < 1. Чем ближе корреляционное отношение к единице, тем теснее связь между изучаемыми признаками.

Рассчитаем г| как меру тесноты связи между заработной платой и выработкой рабочих (см. пример выше). Для этого воспользуемся данными примера 9.2: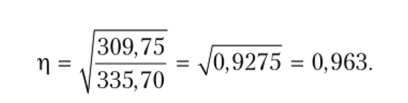

Качественная интерпретация теоретического корреляционного отношения осуществляется на основе шкалы Чеддока:

Следовательно, изучаемые нами признаки: заработная плата и выработка рабочих — связаны достаточно тесно.

Квадрат теоретического корреляционного отношения г² называется коэффициентом детерминации. В нашем примере он равен 0,927 и означает, что 92,7% вариации заработной платы рабочих обусловлено колеблемостью выработки продукции в натуральном выражении.

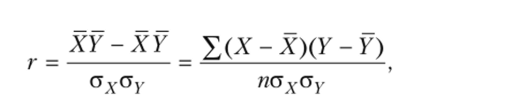
При линейной форме связи помимо теоретического корреляционного отношения для измерения тесноты связи может быть использован линейный коэффициент корреляции, предложенный английским математиком К. Пирсоном:

где п — число наблюдений;

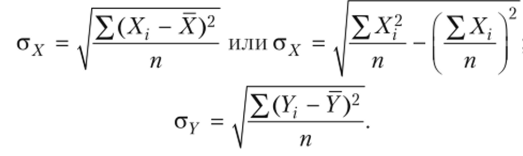
При небольшом числе наблюдений (п < 20-к30) этот коэффициент удобнее вычислять по следующей формуле:

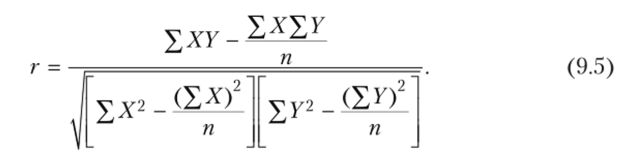
Линейный коэффициент корреляции может принимать значение в интервале: -1 < г < +1.

Отрицательное значение /'указывает на обратную связь, его положительное значение — на прямой характер зависимости. При г — 0 линейная связь отсутствует. Чем ближе коэффициент корреляции к единице (по абсолютной величине), тем теснее связь между изучаемыми признаками. При г = 1 связь функциональная.

Используя данные примера 9.2, рассчитаем линейный коэффициент корреляции по формуле (9.5):

Квадрат линейного коэффициента корреляции называется линейным коэффициентом детерминации. Его значение всегда находится в пределах от нуля до единицы.

Значения теоретического корреляционного отношения ц и линейного коэффициента корреляции г совпадают только при наличии прямолинейной связи. Эта закономерность используется для оценки формы связи. Если разность между г² и г² не превышает 0,1, то связь между изучаемыми признаками можно считать прямолинейной.

В приведенном примере г = г= 0,96, и это значит, что зависимость заработной платы рабочих от выработки продукции в натуральном выражении носит линейный характер.

Для оценки значимости г, так же как и при оценке значимости коэффициентов регрессии, используется^{-критерий} Стыодента. Расчетное значение t при этом определяется по формуле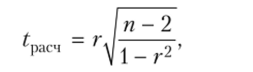

где п — объем выборки.

В нашем примере соответственно:

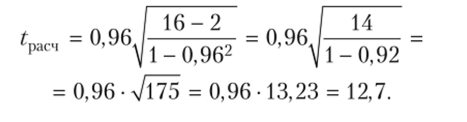
Эго значительно больше, чем критическое значение t = 2,977 при числе степеней свободы 14(16 — 2) и уровне значимости, а = 0,01. Это свидетельствует о значимости коэффициента корреляции и о существенности связи между заработной платой рабочих и выработкой продукции.

Следовательно, регрессионная модель Y = 2,045Х + 2,829 адекватна и ее можно использовать в экономическом анализе.

Такая зависимость означает, что с ростом выработки продукции в данной совокупности рабочих на 1 тыс. шт. в среднем величина их заработной платы увеличивается на 2,8 тыс. руб.

Для интерпретации а_{ можно использовать коэффициент эластичности:

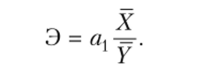
Этот коэффициент показывает среднее изменение результативного признака в процентах при изменении факторного признака на 1%. В нашем примере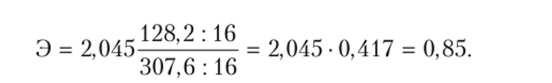

Это означает: при росте выработки продукции на 1% заработная плата рабочих возрастает на 0,85%.

Если данная совокупность и условия работы типичны, то эго уравнение можно использовать для планирования и прогнозирования заработной платы рабочих.

• [1] Проверка адекватности регрессионной модели, как правило, дополняется определением тесноты корреляционной связи между результативными факторным признаками. Для решения этой задачи используется теоретическое корреляционноеотношение: где а2 — общая дисперсия результативного признака, отображающая совокупное влияние всех факторов на вариацию результативного признака У, определяется по формуле
• [2] 2 — факторная дисперсия результативного признака, отображающая вариацию результативного признака У только иод воздействием изучаемогофактора X, определяется по формуле