Луна и звезды у горизонта

Самый невнимательный наблюдатель знает, что полный месяц, стоящий низко у горизонта, имеет заметно большую величину, чем когда он висит высоко в небе. Разница так велика, что трудно ее не заметить. То же верно и для Солнца; известно, как велик солнечный диск при заходе или восходе по сравнению с его размерами высоко в небе, например, когда он просвечивает сквозь облака (прямо смотреть на незатуманенное солнце вредно для глаз).

Для звезд эта особенность проявляется в том, что расстояния между ними увеличиваются, когда они приближаются к горизонту. Кто видел зимою красивое созвездие Ориона (или летом — Лебедя) высоко на небе и низко близ горизонта, тот не мог не поразиться огромной разницей размеров созвездия в обоих положениях.

Все это тем загадочнее, что, когда мы смотрим на светила при восходе или заходе, они не только не ближе, но, напротив, дальше (на величину земного радиуса), как легко понять из рис. 73: в зените мы рассматриваем светило из точки А, а у горизонта — из точек В или С. Почему же Луна, Солнце и созвездия увеличиваются у горизонта?

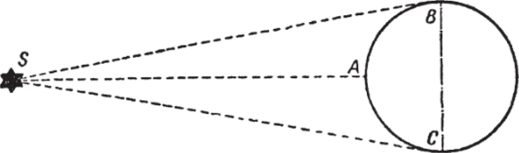
Рис. 73. Почему Солнце, находясь на горизонте, дальше от наблюдателя, чем находясь на середине неба.

«Потому что это неверно», — можно бы ответить. Это обман зрения. При помощи грабельного или иного угломера нетрудно убедиться, что лунный диск виден в обоих случаях под одним и тем же углом зрения^[1] в полградуса. Пользуясь тем же прибором или «посохом Якова», можно удостовериться, что и угловые расстояния между звездами не меняются, где бы созвездие ни стояло: у зенита или у горизонта. Значит, увеличение — оптический обман, которому поддаются все люди без исключения.

Чем объясняется столь сильный и всеобщий обман зрения? Бесспорного ответа на этот вопрос, насколько нам известно, наука еще не дала, хотя и стремится разрешить его 2000 лет, со времени Птолемея. Иллюзия находится в связи с тем, что весь небесный свод представляется нам не полушаром в геометрическом смысле слова, а шаровым сегментом, высота которого в 2—3 раза меньше радиуса основания. Это потому, что при обычном положении головы и глаз расстояния в горизонтальном направлении и близком к нему оцениваются нами как более значительные по сравнению с вертикальными: в горизонтальном направлении мы рассматриваем предмет «прямым взглядом», а во всяком другом — глазами, поднятыми вверх или опущенными вниз. Если Луну наблюдать лежа на спине, то она, наоборот, покажется больше, когда будет в зените, чем тогда, когда она будет стоять низко над горизонтом^[2]. Перед психологами и физиологами стоит задача объяснить, почему видимый размер предмета зависит от ориентации наших глаз.

Что же касается влияния кажущейся приплюснутости небесного свода на величину светил в разных его частях, то оно становится вполне понятным из схемы, изображенной на рис. 74. На своде неба лунный диск всегда виден под углом в полградуса, будет ли. Луна у горизонта (на высоте 0°), или у зенита (на высоте 90°). Но наш глаз относит этот диск не всегда на одно и то же расстояние: Луна в зените отодвигается нами на более близкое расстояние, нежели у горизонта, и потому величина его представляется неодинаковой — внутри одного и того же угла ближе к вершине помещается меньший кружок, чем подальше от нее. На левой стороне того же рисунка показано, как благодаря этой причине расстояния между звездами словно растягиваются с приближением их к горизонту: одинаковые угловые расстояния между ними кажутся тогда неодинаковыми.

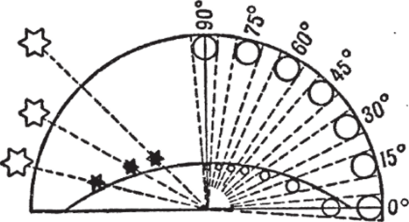
Рис. 74. Влияние приплюснутости небесного свода на кажущиеся размеры светил.

Есть здесь и другая поучительная сторона. Любуясь огромным лунным диском близ горизонта, заметили ли вы на нем хоть одну новую черточку, которой не удалось вам различить на диске высоко стоящей Луны? Нет. Но ведь перед вами увеличенный диск, отчего же нс видно новых подробностей? Оттого, что здесь нет того увеличения, какое дает, например, бинокль: здесь не увеличивается угол зрения, под которым представляется нам предмет. Только увеличение этого угла помогает нам различать новые подробности; всякое иное «увеличение» есть просто обман зрения, для нас совершенно бесполезный^[3].

Какой длины тень Луны н тень стратостата Довольно неожиданное применение для угла зрения найдено мною в задачах на вычисление длины тени, отбрасываемой различными телами в пространстве. Луна, например, отбрасывает в мировом пространстве конус тени, который сопровождает сс всюду.

Как далеко эта тень простирается?

Чтобы выполнить это вычисление, нет необходимости, основываясь на подобии треугольников, составлять пропорцию, в которую входят диаметры Солнца и Луны, а также расстояние между Луной и Солнцем. Расчет можно сделать гораздо проще. Вообразите, что глаз ваш помещен в той точке, где кончается конус лунной тени, в вершине этого конуса, и вы смотрите оттуда на Луну. Что вы увидите? Черный круг Луны, закрывающий Солнце. Угол зрения, под которым виден нам диск Луны (или Солнца), известен: он равен половине градуса. Но мы уже знаем, что предмет, видимый под углом в полградуса, удален от наблюдателя на 2 • 57 = 114 своих поперечников. Значит, вершина конуса лунной тени отстоит от Луны на 114 лунных поперечников. Отсюда длина лунной тени равна.

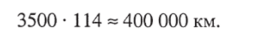
Она длиннее расстояния от Земли до Луны; оттого и могут случаться полные солнечные затмения (для мест земной поверхности, которые погружаются в эту тень).

Нетрудно вычислить и длину тени Земли в пространстве: она во столько раз больше лунной, во сколько раз диаметр Земли превышает диаметр Луны, т. е. примерно в четыре раза.

Тот же прием годен и для вычисления длины пространственных теней более мелких предметов. Найдем, например, как далеко простирался в воздухе конус тени, отбрасываемой стратостатом «СОАХ-1» в тот момент, когда оболочка его раздувалась в шар. Так как диаметр шара стратостата 36 м, то длина его тени (угол при вершине конуса тени тот же, полградуса) или около 4 км.

Во всех рассмотренных случаях речь шла, конечно, о длине полной тени, а не полутени.

• [1] Измерения, произведенные более точными инструментами, показывают, что видимый диаметр Луны даже меньше, когда Луна находится вблизи от горизонта, вследствие того, что рефракция несколько сплющивает диск.
• [2] В предыдущих изданиях «Занимательной геометрии"Я.И. Перельман объяснял кажущееся увеличение Луны у горизонтатем, что у горизонта мы ее видим рядом с отдаленными предметами, а на пустом небесном своде ее видим одну. Однако та же иллюзиянаблюдается и на ничем не заполненном горизонте моря, так чтопредлагавшееся прежде объяснение описываемого эффекта надо признать неудовлетворительным. {Прим. Б. А. Кордемского.)
• [3] Подробнее см. в книге Я. И. Перельмана «Физические головоломки», глава девятая.