Ортогональные сигналы. 
Теория электросвязи

Удобным способом спектрального описания сигнала по Фурье является его аналитическое представление с помощью системы ортогональных элементарных функций времени. Пусть имеется гильбертово пространство сигналов u0(t)y г/,(?), …, un (t) с конечной энергией, определенных на конечном или бесконечном интервале времени (tv 12). На этом отрезке зададим бесконечную систему (подмножество) взаимосвязанных элементарных функций времени и назовем ее базисной'.

где г = 1, 2, 3,…

Функции u (t) и v (t) ортогональны на интервале (?, ?₂), если их скалярное произведение.

при условии что ни одна из этих функций нс равна тождественно нулю.

В математике так задают в гильбертовом пространстве сигналов ортогональный координатный базис, т. е. систему ортогональных базисных функций.

Свойство ортогональности функций (сигналов) связано с интервалом их определения (рис. 2.9). Например, два гармонических сигнала м,(?) = = sin (2nr/7'₀) и u.,(t) = sin (4nt/T_Q) (т.е. с частотами/₀ = 1/7'₀ и 2/₀ соответственно) ортогональны на любом интервале времени, длительность которого равна целому числу полупериодов Т₀ (рис. 2.9, а). Следовательно, в первом периоде сигналы и_{(1) и u₂(t) ортогональны на интервале (0, 7'₀/2); но на интервале (О, ЗГ₀/4) они неортогональны. Па рис. 2.9, б сигналы ортогональны из-за разновременности их появления.

Рис. 2.9. Ортогональность сигналов:

а — на интервале; б — из-за разновременности появления Представление сигнала u (t) элементарными моделями существенно упрощается, если выбрана система базисных функций vff), обладающих свойством ортонормированности. Из математики известно, если для любой пары функций из ортогональной системы (2.7) выполняется условие.

то система функций (2.7) ортонормированна.

В математике такую систему базисных функций вида (2.7) называют ортонормированным базисом.

Пусть на заданном интервале времени |г, t₂ | действует произвольный сигнал u (t) и для его представления используется ортонормированная система функций (2.7). Проектирование произвольного сигнала u (t) на оси координатного базиса называется разложением в обобщенный ряд Фурье. Это разложение имеет вид.

где с, — некоторые постоянные коэффициенты.

Для определения коэффициентов с_к обобщенного ряда Фурье выберем одну из базисных функций (2.7) v_k(t) с произвольным номером к. Умножим обе части разложения (2.9) на эту функцию и проинтегрируем результат по времени:

Вследствие ортонормированности базиса выбранных функций в правой части этого равенства все члены суммы при i ^ к обратятся в нуль. Ненулевым останется только единственный член суммы с номером i = k, поэтому.

Произведение вида c_kv_k(t), входящее в обобщенный ряд Фурье (2.9), представляет собой спектральную составляющую сигнала u (t), а совокупность коэффициентов (проекций векторов сигнала на оси координат) {с₀, с,…, с_к,…, с"} полностью определяет анализируемый сигнал ii (t) и называется его спектром (от лат. spectrum — образ).

Суть спектрального представлениия (анализа) сигнала состоит в определении коэффициентов с_яв соответствии с формулой (2.19).

Выбор рациональной ортогональной системы координатного базиса функций зависит от цели исследований и определяется стремлением максимального упрощения математического аппарата анализа, преобразований и обработки данных. В качестве базисных функций в настоящее время используются полиномы Чебышева, Эрмита, Лагерра, Лежандра и др. Наибольшее распространение получило преобразование сигналов в базисах гармонических функций: комплексных экспоненциальных exp (J 2лft) и вещественных тригонометрических синусно-косинусных функций, связанных формулой Эйлера е^>х = cosx + y’sinx. Это объясняется тем, что гармоническое колебание теоретически полностью сохраняет свою форму при прохождении через линейные цепи с постоянными параметрами, а изменяются при этом лишь его амплитуда и начальная фаза. Также широко используется хорошо разработанный в теории цепей символический метод. Операцию представления детерминированных сигналов в виде совокупности постоянной составляющей (constant component) и суммы гармонических колебаний с кратными частотами принято называть спектральным разложением. Достаточно распространенное использование в теории сигналов обобщенного ряда Фурье связано также с его очень важным свойством: при выбранной ортонормированной системе функций v_k(t) и фиксированном числе слагаемых ряда (2.9) он обеспечивает наилучшее представление заданного сигнала u (t). Это свойство рядов Фурье широко известно.

При спектральном представлении сигналов наибольшее применение получили ортонормированные базисы тригонометрических функций. Это обусловлено следующим: гармонические колебания наиболее просто генерировать; гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями.

Оценим временное и спектральное представления аналогового сигнала (рис. 2.10). На рис. 2.10, а показана временная диаграмма сложного по форме непрерывного сигнала, а на рис. 2.10, б — его спектральное разложение.

Рассмотрим спектральное представление периодических сигналов в виде суммы либо гармонических функций, либо комплексных экспонент с частотами, образующими арифметическую прогрессию.

Периодическим называют сигнал и"(?). повторяющийся через регулярные интервалы времени (рис. 2.11):

где Г — период повторения или следования импульсов; п = 0, 1, 2,…

Рис. 2.10. Спектральное представление аналогового сигнала:

а — временная диаграмма; 6 — амплитудный спектр

Рис. 2.11. Периодический сигнал.

Если Т является периодом сигнала u (t), то периодами будут и кратные ему значения: 2Т, 3Т и т. д. Периодическая последовательность импульсов (их называют видеоимпульсами) описывается выражнением.

Здесь u₀(t) — форма одиночного импульса, характеризующаяся амплитудой (высотой) h = Е, длительностью т", периодом следования Т= /F (F — частота), положением импульсов во времени относительно тактовых точек, например t = 0.

При спектральном анализе периодических сигналов удобна ортогональная система (2.7) в виде гармонических функций с кратными частотами:

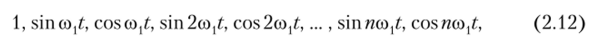
где со, = 2п/Т— частота следования импульсов.

Вычисляя интегралы, по формуле (2.8) легко убедиться в ортогональности этих функций на интервале [-Г/2, Г/2]. Любая функция удовлетворяет условию периодичности (2.11), поскольку частоты их кратны. Если систему (2.12) записать как.

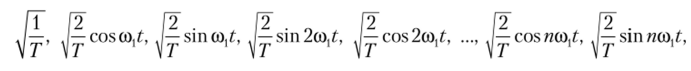
то получим ортонормированный базис гармонических функций.

Представим периодический сигнал наиболее распространенной в теории сигналов тригонометрической (синусно-косинусной) формой ряда Фурье:

Из курса математики известно, что разложение (2.11) существует, т. е. ряд сходится, если функция (в данном случае сигнал) u (t) на интервале [-7/2, 7/2] удовлетворяет условиям Дирихле (в отличие от теоремы Дирихле их часто трактуют упрощенно):

• • не должно быть разрывов 2-го рода (с уходящими в бесконечность ветвями);
• • функция ограничена и имеет конечное число разрывов 1-го рода (скачков);
• • функция имеет конечное число экстремумов (т.е. максимумов и минимумов).

В формуле (2.13) имеются следующие компоненты анализируемого сигнала:

• постоянная составляющая.

• амплитуды косинусоидальных составляющих.

• амплитуды синусоидальных составляющих.

Спектральную составляющую с частотой со, в теории связи называют первой (основной) гармоникой, а составляющие с частотами исо, (п > 1) — высшими гармониками периодического сигнала. Шаг по частоте Асо между двумя соседними синусоидами из разложения Фурье называют частотным разрешением спектра.

Если сигнал представляет собой четную функцию времени u (t) = u (-t), то в тригонометрической записи ряда Фурье (2.13) отсутствуют синусоидальные коэффициенты Ь_п, так как в соответствии с формулой (2.16) они обращаются в нуль. Для сигнала u (t), описываемого нечетной функцией времени, наоборот, согласно формуле (2.15) нулю равны косинусоидальные коэффициенты а_п (постоянная составляющая а₀ также отсутствует), и ряд содержит составляющие Ь_п.

Пределы интегрирования (от -7/2 до 7/2) не обязательно должны быть такими, как в формулах (2.14)—(2.16). Интегрирование может производиться по любому интервалу времени шириной 7 — результат от этого не изменится. Конкретные пределы выбираются из соображений удобства вычислений; например, может оказаться проще выполнять интегрирование от О до 7 или от -7 до 0 и т. д.

Раздел математики, устанавливающий соотношение между функцией времени u (t) и спектральными коэффициентами а_п, Ь_п, называют гармоническим анализом вследствие связи функции u (t) с синусоидальными и косинусоидальными членами этой суммы. Далее спектральный анализ в основном ограничен рамками гармонического анализа, находящего исключительное применение.

Часто применение синусно-косинусной формы ряда Фурье не совсем удобно, поскольку для каждого значения индекса суммирования п (т.е. для каждой гармоники с частотой mOj) в формуле (2.13) фигурируют два слагаемых — косинус и синус. С математической точки зрения удобнее эту формулу представить эквивалентным рядом Фурье в вещественной форме/.

где А₀ = а₀/2; А_п = yja²_n + Ь — амплитуда; <�р_я = arctg (6_J/fl_ll) — начальная фаза п-й гармоники сигнала. Иногда в соотношении (2.17) перед ср_Л ставят знак «плюс», тогда начальную фазу гармоник записывают как ср_и = -arctg (b_nfa_n).

В теории сигналов широко используют комплексную форму ряда Фурье. Она получается из вещественной формы ряда представлением косинуса в виде полусуммы комплексных экспонент по формуле Эйлера:

Применив данное преобразование к вещественной форме ряда Фурье (2.17), получим суммы комплексных экспонент с положительными и отрицательными показателями:

А теперь будем трактовать в формуле (2.19) экспоненты при частоте со, со знаком «минус» в показателе как члены ряда с отрицательными номерами. В рамках этого же подхода коэффициент А₀ станет членом ряда с нулевым номером. После несложных преобразований приходим к комплексной форме ряда Фурье.

где.

— комплексная амплитуда п-й гармоники.

Значения С_п по положительным и отрицательным номерам п являются комплексно-сопряженными.

Отметим, что ряд Фурье (2.20) представляет собой ансамбль комплексных экспонент exp (jn (o_{t) с частотами, образующими арифметическую прогрессию.

Определим связь между коэффициентами тригонометрической и комплексной форм ряда Фурье. Очевидно, что.

Можно также показать, что коэффициенты а_п = 2C_wcoscp"; b_n = 2C_/Isincp,_f.

Если u (t) является четной функцией, коэффициенты ряда С, будут вещественными, а если u (t) — функция нечетная, коэффициенты ряда станут мнимыми.

Спектральное представление периодического сигнала комплексной формой ряда Фурье (2.20) содержит как положительные, так и отрицательные частоты. Но отрицательные частоты в природе не существуют, и это математическая абстракция (физический смысл отрицательной частоты — вращение в направлении, противоположном тому, которое принято за положительное). Они появляются как следствие формального представления гармонических колебаний комплексной формой. При переходе от комплексной формы записи (2.20) к вещественной (2.17) отрицательная частота пропадает.

Наглядно о спектре сигнала судят, но его графическому изображению — спектральной диаграмме (рис. 2.12). Различают амплитудно-частотные и фазо-частотные спектры. Совокупность амплитуд гармоник А_п (рис. 2.12, а) называют амплитудным спектром, их фаз (рис. 2.12, б) ср_я — фазовым спектром. Совокупность С_п = |С_п является комплексным амплитудным спектром (рис. 2.12, в). На спектральных диаграммах, но оси абсцисс откладывают текущую частоту, а, но оси ординат — либо вещественную, либо комплексную амплитуду или фазу соответствующих гармонических составляющих анализируемого сигнала.

Рис. 2.12. Спектры периодического сигнала:

а — амплитудный; б — фазовый; в — амплитудный спектр комплексного ряда Фурье Спектр периодического сигнала называют линейчатым или дискретным, так как он состоит из отдельных линий с высотой, равной амплитуде А_п гармоник. Из всех видов спектров наиболее информативен амплитудный, поскольку он позволяет оценить количественное содержание тех или иных гармоник в частотном составе сигнала. В теории сигналов доказано, что амплитудный спектр есть четная функция частоты, а фазовый — нечетная.

Отметим эквидистантность (равноудаленность от начала координат) комплексного спектра периодических сигналов: симметричные (положительные и отрицательные) частоты, на которых расположены спектральные коэффициенты тригонометрического ряда Фурье, образуют эквидистантную последовательность (…, -жo_v …, -2со_р -со_р 0, _v 2со, …, nco_v …), содержащую частоту со = 0 и имеющую шаг co_t = 2л/7'. Коэффициенты могут принимать любые значения.

Пример 2.1.

Рассчитаем амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов с амплитудой ?, длительностью т_и и периодом повторения Т. Сигнал — функция четная (рис. 2.13).

Рис. 2.13. Последовательность прямоугольных импульсов.

Решение

Известно, что идеальный прямоугольный видеоимпульс описывается следующим уравнением:

т.е. он формируется как разность двух единичных функций а (?) (функций включения), сдвинутых во времени на т_н.

Последовательность прямоугольных импульсов представляет собой известную сумму одиночных импульсов:

Поскольку заданный сигнал является четной функцией времени и в течение одного периода действует только на интервале [т_и/2, т_и/2], то согласно формуле (2.14).

где q = Т/ т".

Анализируя полученную формулу, можно заметить, что период следования и длительность импульсов входят в нее в виде отношения. Этот параметр q — отношение периода к длительности импульсов — называют скважностью периодической последовательности импульсов (в зарубежной литературе вместо скважности используют обратную величину — коэффициент заполнения, от англ, duty cycle, равный т_и/7); при q = 2 последовательность прямоугольных импульсов, когда длительности импульсов и промежутков между ними становятся равными, называют меандром (от греч. paiav5poq — узор, геометрический орнамент).

В силу четности функции, описывающей анализируемый сигнал, в ряде Фурье наряду с постоянной составляющей будут присутствовать только косинусоидальные составляющие (2.15):

В правой части формулы (2.22) второй сомножитель имеет вид элементарной функции (sinx)/x. В математике эту функцию обозначают как sinc (x), причем только при значении х = 0 она равна единице (lim (sinx/x) =1), проходит л^О через нуль в точках х = ±л, ±2л,… и затухает с ростом аргумента х (рис. 2.14). Окончательно тригонометрический ряд Фурье (2.13), который аппроксимирует заданный сигнал, записывают в форме

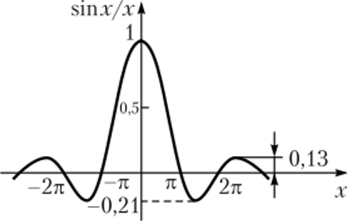
Рис. 2.14. График функции sinx/x.

Функция sine имеет лепестковый характер. Говоря о ширине лепестков, следует подчеркнуть, что для графиков дискретных спектров периодических сигналов возможны два варианта градуировки горизонтальной оси — в номерах гармоник и частотах. Например, на рис. 2.14 градуировка оси ординат соответствует частотам. Ширина лепестков, измеренная в числе гармоник, равна скважности последовательности. Отсюда следует важное свойство спектра последовательности прямоугольных импульсов — в нем отсутствуют (имеют нулевые амплитуды) гармоники с номерами, кратными скважности. При скважности импульсов, равной трем, исчезает каждая третья гармоника. Если бы скважность была бы равна двум, то в спектре остались бы лишь нечетные гармоники основной частоты.

Из формулы (2.22) и рис. 2.14 следует, что коэффициенты ряда высших гармоник сигнала имеют отрицательный знак. Это связано с тем, что начальная фаза этих гармоник равна п. Поэтому формулу (2.22) принято представлять в измененном виде:

При такой записи ряда Фурье значения амплитуд всех высших гармонических составляющих на графике спектральной диаграммы положительны (рис. 2.15, а).

Амплитудный спектр сигнала в значительной степени зависит от отношения периода повторения Т и длительности импульса т_и, т. е. от скважности q. Расстояние по частоте между соседними гармониками равно частоте следования импульсов со₁ = 2л/'Г. Ширина лепестков спектра, измеренная в единицах частоты, равна 2я/т_н, т. е. обратно пропорциональна длительности импульсов. Отметим, что при одной и той же длительности импульса т_и с увеличением не;

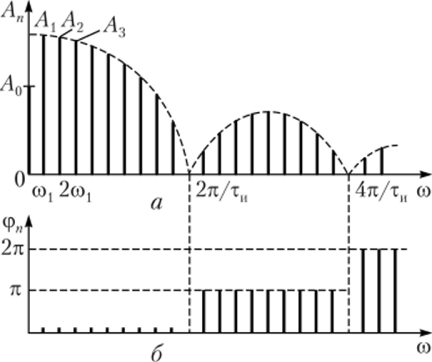
Рис. 2.15. Спектры последовательности прямоугольных импульсов:

а — амплитудный; б — фазовый риода их повторения Т основная частота со, уменьшается и спектр становится плотнее.

Ту же картину наблюдают, если укорачивают длительность импульса т_и при неизменном периоде Т. Амплитуды всех гармоник при этом уменьшаются. Это проявление общего закона (принципа неопределенности В. Гейзенберга — Uncertainty principle): чем короче длительность сигнала, тем шире его спектр.

Фазы составляющих определим из формулы ф_л = arctg(b_n/a_n). Так как здесь коэффициенты Ь" = 0, то.

где m = 0, 1, 2,…

Соотношение (2.24) показывает, что при вычислениях фаз спектральных составляющих имеем дело с математической неопределенностью. Для ее раскрытия обратимся к формуле (2.22), согласно которой амплитуды гармоник периодически меняют знак в соответствии с изменением знака функции sin (nco₁x_1I/2). Изменение знака в формуле (2.22) эквивалентно сдвигу фазы этой функции на п. Следовательно, когда данная функция положительна, фаза гармоники ф_и = 2тп, а когда отрицательна — ф" = (2т + 1 )к (рис. 2.15, б). Заметим, что хотя амплитуды составляющих в спектре прямоугольных импульсов и уменьшаются с ростом частоты (см. рис. 2.15, а), этот спад довольно медленный (амплитуды убывают обратно пропорционально частоте). Для передачи таких импульсов без искажений необходима бесконечная полоса частот канала связи. Для сравнительно малозаметных искажений граничное значение полосы частот должно быть во много раз больше значения, обратного длительности импульса. Однако все реальные каналы имеют конечную полосу пропускания, что приводит к искажениям формы переданных импульсов.

Ряды Фурье произвольных периодических сигналов могут содержать бесконечно большое количество членов. При расчетах спектров таких сигналов вычисление бесконечной суммы ряда Фурье вызывает определенные трудности и не всегда требуется, поэтому ограничиваются суммированием конечного количества слагаемых (ряд «усекают»).

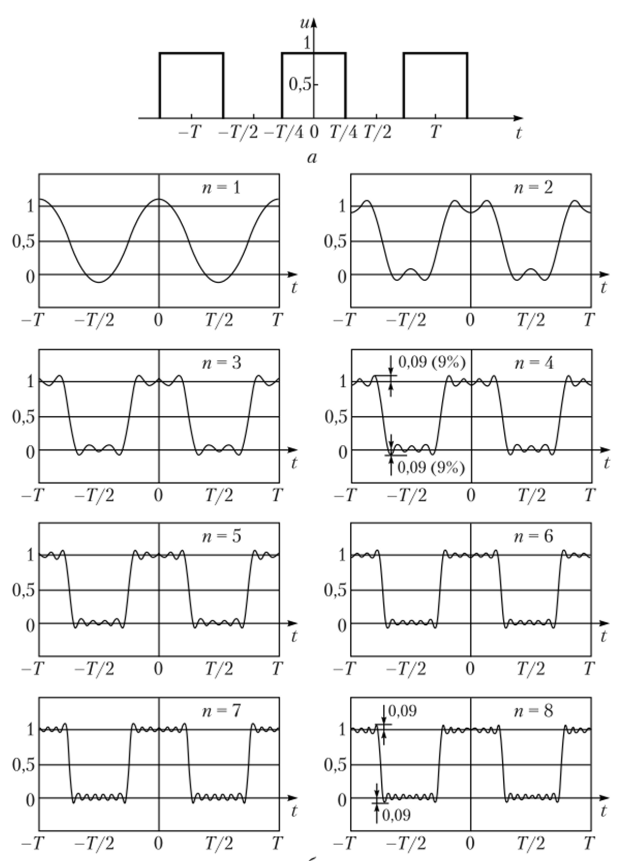
Точность аппроксимации сигнала зависит от числа суммируемых составляющих. Рассмотрим это на примере аппроксимации суммой из восьми первых гармоник последовательности прямоугольных импульсов (рис. 2.16). Сигнал имеет вид однополярного меандра с периодом повторения Т_у амплитудой Е = 1 и длительностью импульсов т_и = Т/2 (заданный сигнал — функция четная — рис. 2.16, а; скважность q = 2). Аппроксимация показана на рис. 2.16, б, причем на графиках показано число суммируемых гармоник. В проводимой аппроксимации заданного периодического сигнала (см. рис. 2.13) тригонометрическим рядом (2.13) суммирование первой и высших гармоник будет осуществляться только по нечетным коэффициентам Пу так как при четных их значениях и длительности импульса т_и = Т/2 = = 7т/со₁ величина sin (mo, T_H/2) = sin (wt/2) обращается в нуль.

Тригонометрическая форма ряда Фурье (2.23) для заданного сигнала имеет вид.

о.

Рис. 2.16. Формирование меандра суммой гармоник ряда Фурье:

а — заданный сигнал; б — промежуточные стадии суммирования Для удобства представления ряд Фурье (2.25) можно записать упрощенно:

Из формулы (2.26) очевидно, что гармоники, аппроксимирующие меандр, нечетны, имеют чередующиеся знаки, а их амплитуды обратно пропорциональны номерам. Отметим, что последовательность прямоугольных импульсов плохо подходит для представления рядом Фурье — аппроксимация содержит пульсации и скачки, а сумма любого числа гармонических составляющих с любыми амплитудами всегда будет непрерывной функцией. Поэтому поведение ряда Фурье в окрестностях разрывов представляет особый интерес. Из графиков рис. 2.16, 6 нетрудно заметить, как с увеличением числа суммируемых гармоник результирующая функция все точнее приближается к форме исходного сигнала u{t) везде, кроме точек ее разрыва. В окрестности точек разрыва суммирование ряда Фурье дает наклонный участок, причем крутизна наклона результирующей функции возрастает с увеличением числа суммируемых гармоник. В самой точке разрыва (обозначим ее как t = t₀) ряд Фурье u (t₀) сходится к полусумме правого и левого пределов:

На примыкающих к разрыву участках аппроксимируемой кривой сумма ряда дает заметные пульсации, причем на рис. 2.16 видно, что амплитуда основного выброса этих пульсаций не уменьшается с ростом числа суммируемых гармоник — он лишь сжимается по горизонтали, приближаясь к точке разрыва.

При п —? в точках разрыва амплитуда выброса остается постоянной, а его ширина будет бесконечно узкой. Не изменяются и относительная амплитуда пульсаций (по отношению к амплитуде скачка), и относительное затухание; изменяется только частота пульсаций, которая определяется частотой последних суммируемых гармоник. Это связано со сходимостью ряда Фурье. Обратимся к классическому примеру: достигнете ли вы когда-нибудь стены, если с каждым шагом будете проходить половину оставшегося расстояния? Первый шаг приведет к отметке половины пути, второй — к отметке на трех его четвертях, а после пятого шага пройдете уже почти 97% пути. Вы почти дошли до цели, однако сколько бы вы еще шагов вперед ни сделали, никогда не достигнете ее в строгом математическом смысле. Можно лишь доказать математически, что в конце концов вы сможете приблизиться на любое заданное сколь угодно малое расстояние. Данное доказательство будет эквивалентно демонстрации того, что сумма чисел ½, 1/4,1/8,1/16 и т. д. стремится к единице. Это явление, присущее всем рядам Фурье для сигналов с разрывами 1-го рода (например, скачками, как на фронтах прямоугольных импульсов), называют эффектом Гиббса*. При этом значение первого (самого большого) выброса амплитуды в аппроксимируемой кривой составляет около 9% уровня скачка (см. рис. 2.16, п = 4).

Эффект Гиббса приводит к неустранимой погрешности аппроксимации периодических импульсных сигналов с разрывами 1-го рода. Эффект имеет место при резких нарушениях монотонности функций. На скачках эффект максимален, во всех других случаях амплитуда пульсаций зависит от характера нарушения монотонности. Для ряда практических приложений эффект Гиббса вызывает определенные проблемы. Например, в звуковоспроизводящих системах это явление называют «звоном» или «дребезгом». При этом каждый резкий согласный или другой внезапный звук может сопровождаться коротким неприятным для слуха звуком.

Ряд Фурье может быть применен не только для периодических сигналов, но и для сигналов конечной длительности. При этом оговаривается времен-^[1]

ной интервал, для которого строится ряд Фурье, а в остальные моменты времени сигнал считается равным нулю. Для расчета коэффициентов ряда такой подход означает периодическое продолжение сигнала за границами рассматриваемого интервала.

Отметим, что и природа (например, слух человека) использует принцип гармонического анализа сигналов. Виртуальное преобразование Фурье человек производит всякий раз, когда слышит звук: ухо автоматически выполняет это, представляя звук в виде спектра последовательных значений громкости для тонов различной высоты. Мозг человека превращает эту информацию в воспринимаемый звук.

Гармонический синтез. В теории сигналов наряду с гармоническим анализом сигналов широко используют гармонический синтез — получение заданных колебаний сложной формы путем суммирования ряда гармонических составляющих их спектра. По существу выше был проведен синтез периодической последовательности прямоугольных импульсов суммой из ряда гармоник. На практике эти операции выполняют на компьютере, как это показано на рис. 2.16, б.

• [1] Джозайя Гиббс (J. Gibbs, 1839—1903) — американский физик и математик, один из основоположников химической термодинамики и статистической физики.