Игры с непротивоположными интересами. 
Равновесие Нэша. 
Парето-оптимальность

Определение 2.10. Пусть задана игра G в нормальной форме (N, Sj, Исход s = (s, s₂> •••> %)е5 называется равновесием

Нэша (NE — Nash Equilibrium) игры G, если Vi е 1…N, Уу, е 5,.

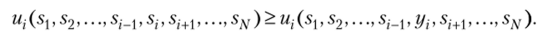
Иначе говоря, каждый из игроков максимизирует свою функцию полезности.

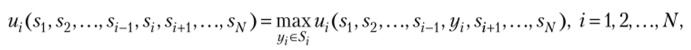
на множестве своих стратегий.

В точке равновесия Нэша стратегия х, — — одна из лучших для игрока i стратегий в ответ на х__; =(х₁, х₂,—.,^_₁, х₁₊₁,…, х_лг) — стратегии остальных игроков. Игрок i рассматривает стратегии из х__; как заданную вполне определенную совокупность стратегий «внешнего мира», на которую он не может активно воздействовать. Он может активно выбирать лишь свою стратегию в, которая будет наилучшим выбором, если остальные игроки выберут s_j. При этом игрок i полагает, что аналогично выбирают свои стратегии и все остальные игроки.

В точке равновесия Нэша игроку i невыгодно в одиночку отклоняться от стратегии s_it если остальные игроки придерживаются стратегий 5₁, s₂,…s,-_₁, s_i+1 …s_N. Действия «в одиночку» могут только уменьшить выигрыш игрока i. Поиск точки равновесия Нэша, таким образом, сводится к решению системы из N задач максимизации функций полезности по соответствующим переменным.

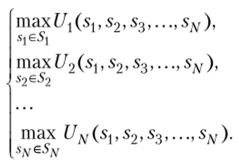
Пусть G — (N, 5,-, Uj, i —1,.N) — конечная игра в нормальной форме.

Назовем X, — множеством смешанных стратегий игрока i, а множество X = X,-Х₂-…-X_jV — множеством профилей всех смешанных стратегий. Обозначим аеХ — элементы этого множества.

Назовем игру G = (N; X; и) смешанным расширением игры G. Тогда равновесие в смешанных стратегиях в игре G — это равновесие Нэша в ее смешанном расширении.

Пример 2.17. Задана биматричная игра.

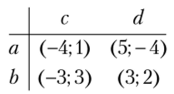
Какие выигрыши будут у игроков при выборе ими стратегий т = 0, а + 0,6Ь и п = 0,25с + 0,75d ?

Решение

Запишем рядом с чистыми стратегиями вероятности их выбора:

Поскольку выбор стратегий осуществляется игроками независимо, вероятность профиля (а; с) равна 0,4−0,25 = 0,1. Аналогично рассчитываются вероятности выигрышей игроков при остальных наборах чистых стратегий. Для удобства выигрыши игроков представим в виде вектор-столбца:

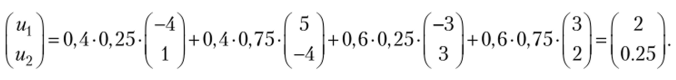
Ответ: щ — 2; и₂ = 0,25.

Наряду с равновесием Нэша введем еще одно важное понятие — доминирования по Парето.

Пусть задана игра в нормальной форме G = (N, Si, u_iti = l,…, N). Рассмотрим два профиля стратегий x = (x, x₂,…, x_jY)e5 и i/ = (i/_vi/₂,…, yy)&S.

Определение 2.11. Профиль стратегий х доминирует по Парето профиль стратегий у, если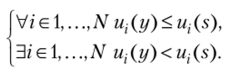

Последняя система неравенств означает, что для всех игроков профиль х не хуже, чем профиль у, но при этом хотя бы для одного из игроков профиль х лучше, чем у.

Определение 2.12. Профиль стратегий х называется оптимальным по Парето (Парето-оптимальным), если он недоминируем, но Парето.

Если исход оптимален, но Парето, то он характеризуется следующим свойством: невозможно улучшить положение ни одного из игроков без ухудшения положения хотя бы одного из других игроков.

Пример 2.18. Найти точки равновесия Нэша, точки равновесия в строго доминирующих стратегиях и Парето-оптимальные точки в матричной игре двух игроков с заданными платежными матрицами:

Решение.

Очевидно, ни одна из стратегий не является строго доминируемой. Поэтому равновесия в строго доминирующих стратегиях нет.

Для определения равновесий Нэша подчеркнем наибольшие выигрыши каждого из игроков при фиксированных ходах противника:

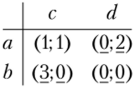
Исходы с двойными подчеркиваниями будут равновесиями Нэша: (a; d) (b; с); (b;d).

Для определения Парето-оптимальных исходов удобно изобразить все точки биматричной игры в критериальной плоскости (рис. 2.21 — по осям откладываем выигрыши игроков).

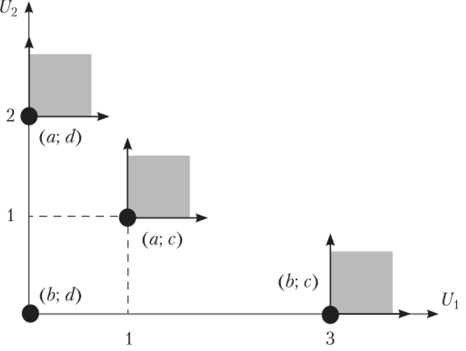
Рис. 2.21.

Парето-оптимальными являются точки, в направлении штриховки от которых (к «северо-востоку») нет других точек. Таковыми являются исходы (а; d) (а; с); (Ь; с). Введем для краткости обозначения для Паретооптимальных точек — Р и для равновесных по Нэшу — N. Получим.

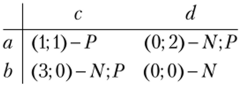
Выясним, существуют ли в этой игре равновесные по Нэшу профили смешанных стратегий.

Пусть стратегии а и b играются с вероятностями р и 1 — р соответственно, а стратегии с и d — с вероятностями q и 1 — q. Запишем матрицу ожидаемых выигрышей первого и второго игроков:

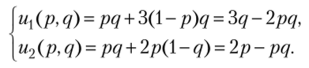
Максимизируем функцию щ (р, q) = 3q — 2pq по переменной р е [0; 1 ] при постоянном значении q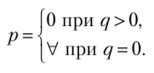

К аналогичному результату приводит рассмотрение рационального поведения второго игрока, оптимизирующего u₂(p, q) по переменной q при постоянном значении р

Изобразим полученный результат 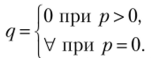(рис. 2.22) в координатах (q, р):

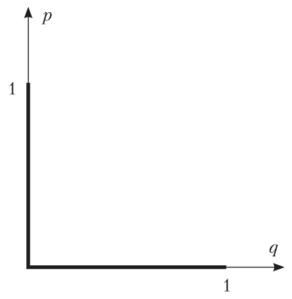
Рис. 2.22.

Как видим, оба графика совпали.

Равновесия Нэша: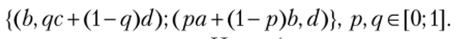

Пример 2.19. Найти точки равновесия Нэша (в смешанных стратегиях) и Парето-оптимальные точки в матричной игре двух игроков с заданными платежными матрицами: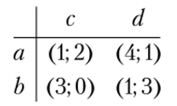

Решение

Очевидно, доминирующих стратегий в игре нет. Точек равновесия Нэша в чистых стратегиях также нет. Парето-оптимальные профили: (а; d) и {b d).

Рассмотрим смешанные стратегии игроков.

Пусть стратегии а и b играются с вероятностями р и 1 — р соответственно, а стратегии cud — с вероятностями q и 1 — q. Запишем матрицу ожидаемых выигрышей первого и второго игроков:

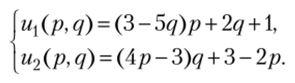
Очевидно, первый игрок решает задачу.

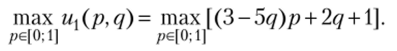
Решением задачи является.

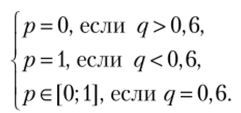
Эти три случая представлены на рис. 2.23.

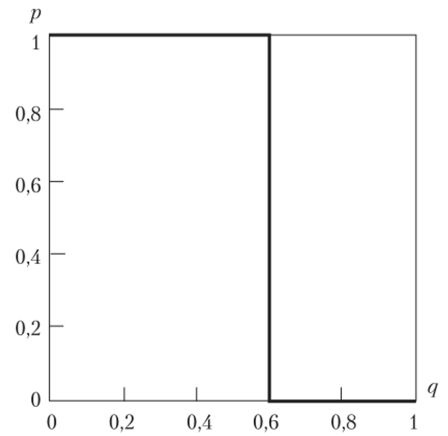
Рис. 2.23.

Аналогично второй игрок решает задачу 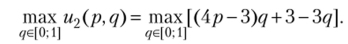Решением задачи является.

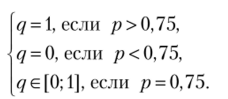
Эти три случая представлены на рис. 2.24.

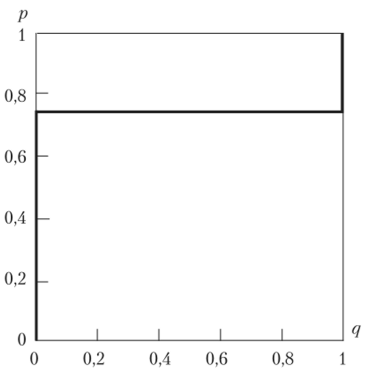
Рис. 2.24.

Совмещая рисунки, получим рис. 2.25.

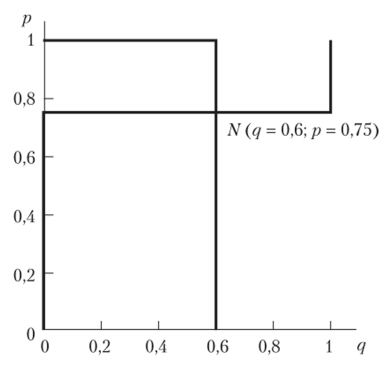
Рис. 2.25.

Точка N (р = 0,75; q = 0,6), очевидно, является точкой равновесия Нэша в смешанных стратегиях, поскольку она получена в результате решения задач максимизации функции u_x(p, q) пори u₂(p, q) по q.

Ответ: равновесие Нэша: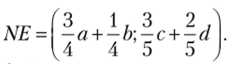

Как соотносятся между собой решения игр в чистых стратегиях, полученные методом итерационного исключения строго доминируемых стратегий (если они существуют) и равновесий Нэша? Ответ на этот вопрос дают следующие две теоремы.

Теорема 2.3. Если существует процедура итерационного исключения строго доминируемых стратегий в игре G — (S;, щ;i —1,…,N), которая приводит к единственному исходу s = (s_i, s₂,…, s_N), то этот исход является единственным равновесием Нэша.

Доказательство теоремы достаточно очевидно, поскольку процедура итерационного исключения строго доминируемых стратегий в конечной игре не может исключить равновесия Нэша. И в силу единственности получаемого исхода он будет единственным равновесием Нэша.

Замечание. Если в теореме 2.3 исключить слово «строго», то она перестает быть справедливой. Например, в игре.

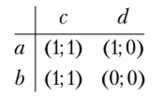
исходы (а; с) и (Ь; с) являются точками равновесия Нэша, хотя стратегия b доминируема.

Теорема 2.4. Если исход явля

ется равновесием Нэша, то он не может быть исключен в процедуре итерационного исключения строго доминируемых стратегий.

Доказательство теоремы следует из определения строгой доминируемости стратегии.

Пример 2.20. Рассмотрим матричную игру:

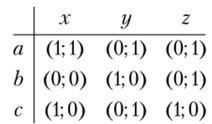
Точка равновесия Нэша — (а, х). Однако стратегия а первого игрока доминируема (не строго) стратегией с, а стратегия х второго игрока доминируема стратегией у. Тем самым мы показали, что условие строгой доминируемое™ в теореме существенно.

Пример 2.21. Рассмотрим игру двух игроков, называемую «битва полов» (или «семейный спор»). Саша и Маша пытаются решить, как им проводить выходной день, — пойти на футбол или на балет. Конечно, Саше больше хочется пойти на футбол, Маша же получает большее удовольствие от балета. Но совсем никакого удовольствия они не получат, если будут развлекаться порознь (бывает же такое!). Саша и Маша выбирают место развлечения одновременно и независимо друг от друга, не сговариваясь. Матрица выигрышей имеет следующий вид^[1]: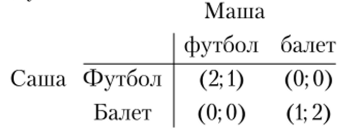

В данной игре исход (Футбол; футбол) является точкой равновесия Нэша. Это значит, что если игроки договорились о выборе каждым из них первой стратегии, то ни одному из них невыгодно будет отклоняться от нее, если другой ее придерживается. Аналогично и исход (Балет; балет) будет точкой равновесия Нэша. Рассмотрим теперь возможность выбора игроками смешанных стратегий. Пусть первый игрок (Саша) выбирает первую и вторую чистые стратегии с вероятностями соответственно р и 1 — р. Второй игрок (Маша) выбирает первую и вторую чистые стратегии с вероятностями соответственно q и 1 -q. Получаем матрицу.

Выигрыш Саши равен.

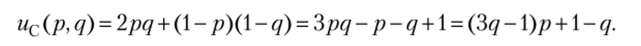
Стратегия Саши определяется выбором вероятности р. Функция выигрыша Саши и_с(р, q) является монотонно возрастающей по переменной р,.

если 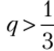, и, следовательно, приСаша выберет максимальное значение вероятности, т. е.р = 1.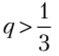

Аналогично если, то функция u_c(p, q) — убывающая по переменной/;, и, следовательно, 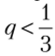при 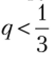Саша, максимизируя свой выигрыш, выберет минимальное значение вероятности, т. е. р = 0.

При 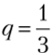функция и_с (р> q) не зависит от р и Сашу удовлетворяет любое значение р е [0; 1]. Таким образом, имеем.

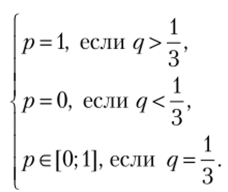
Все сказанное наглядно представляется диаграммой (рис. 2.26).

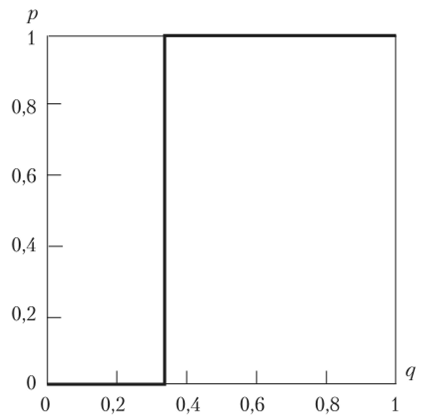
Рис. 2.26.

Выигрыш Маши равен

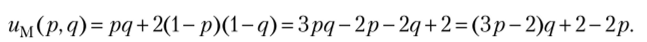
Стратегия Маши определяется выбором вероятности q. Функция выигрыша Маши u_M(p, q) является монотонно возрастающей по переменной q,

если 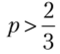, и, следовательно, приМаша выберет максимальное значение вероятности, т. е.q = 1.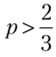

Аналогично если 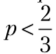, то функция u_M(p, q) — убывающая по переменной q, и, следовательно, приМаша выберет минимальное значение вероятности, т. е. <7 = 0.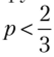

При 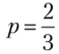функция и_и(р, q) не зависит от q и Машу удовлетворяет любое значение <7 е [0; 1].

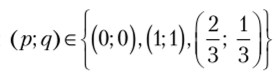
Все сказанное наглядно представляется диаграммой (рис. 2.27). Совмещение диаграмм на рис. 2.26 и 2.27 дает три точки пересечения наилучших выборов игроков на всевозможные действия другого игрока (рис. 2.28).

Имеем три точки равновесия Нэша. Первые две из них соответствуют выбору чистых стратегий (Балет; балет) и (Футбол; футбол). Третья точка представляет собой точку равновесия Нэша в смешанных стратегиях.

Заметим, что значения платежных функций обоих игроков в точке 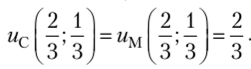В соседней точке, например 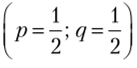, значения платежных функций игроков равны 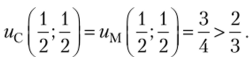Однако эта точка не будет точкой равновесия, поскольку если Маша будет придерживаться стратегии 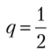, то Саше будет более выгодна стратегия р = 1,.

поскольку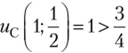

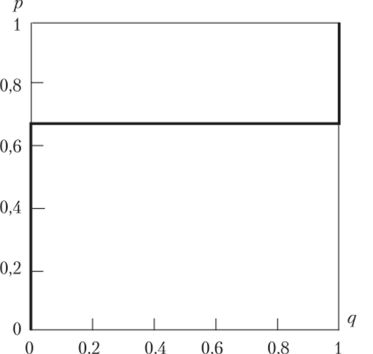
Рис. 2.27 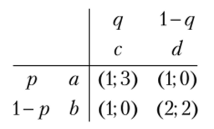Рис. 2.28

Пример 2.22. Рассмотрим пример биматричной игры, в которой существует бесконечно много равновесий 11эша:

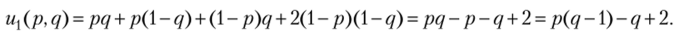
Выигрыш первого игрока равен.

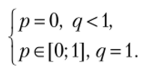
Из условия максимизации функции выигрыша по переменнойр получим.

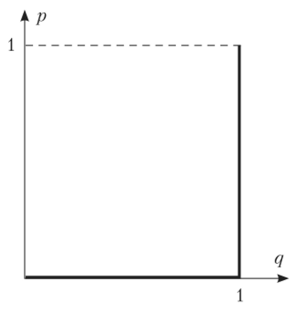
Графически этот выбор изображается следующим образом (рис. 2.29).

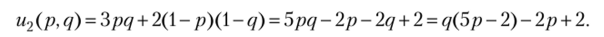
Рис. 2.29.

Это наилучшее для первого игрока действие, зависящее от выбора вероятности q вторым игроком. Но первый игрок не знает, каков выбор второго игрока. Он лишь знает, что второй игрок будет также максимизировать свою функцию выигрыша по переменной q.

Выигрыш второго игрока равен.

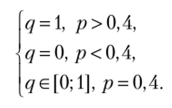
Из условия максимизации функции выигрыша по переменной q получим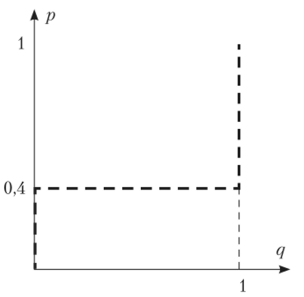

Графически этот выбор изображается следующим образом (рис. 2.30).

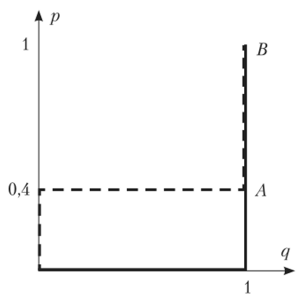
Рис. 230.

Совместим графики на рис. 2.29 и 2.30 (рис. 2.31).

Рис. 2.31.

Графики совпадают на отрезке АВ и в начале координат. Все эти точки и будут равновесиями Нэша в смешанных стратегиях. Точка p = q = 0 означает выбор профиля чистых стратегий (b;d). Поэтому получим: NE:{(b;d), (pa + (l-p)b; с), ре[0,4; 1]}.

Следующая теорема дает ответ на вопрос о существовании равновесия Нэша в довольно широком классе игр.

Теорема 2.5 (Нэш, 1950). Для любой конечной игры (т.е. множество игроков и множества их чистых стратегий конечны) в нормальной форме G = (N, S_jt Uj, i = 1,…, N) всегда существует по крайней мере одна точка равновесия Нэша, возможно, в смешанных стратегиях.

Чистые стратегии могут быть строго доминируемы смешанными стратегиями, даже если в чистых стратегиях не существует доминируемых стратегий. Покажем это на следующем примере.

Пример 2.23. Дана биматричная игра:

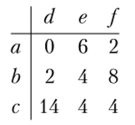
Найти все равновесия Нэша в смешанных стратегиях.

Решение

В данной биматричной игре невозможно, рассматривая только чистые стратегии игроков, исключить строго доминируемые стратегии. Попробуем найти смешанную стратегию, которая доминирует чистую стратегию.

Сначала рассмотрим возможность исключения строго доминируемых строк. Выпишем для удобства матрицу выигрышей первого игрока (он выбирает строки):

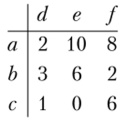
Очевидно, никакая смешанная стратегия ра + (1- р) Ь не сможет доминировать чистую стратегию с, поскольку неравенство /?-0 + (1-/?)-2>14 невыполнимо ни при каких значениях р е [0; 1]. Значит, стратегия с не может быть строго доминируема даже с применением смешанных стратегий.

Как было доказано выше, величина f (p) = p-A + (l-p) B при /?е[0;1], {А и В — действительные числа) может принимать все значения между числами А и В. Действительно, поскольку /(/?) — линейная функция, то множеством ее значений является отрезок E (f) = [min (A; В); шах (Л: В). Например, если /(р) = /? • 2 + (1 — /?) • 5, то Д (/) = [2;5].

Аналогично стратегия а не может быть доминируема смешанной стратегией pb + (l-р)с, поскольку (при выборе вторым игроком стратегии е) потребуется выполнение неравенства 4/?+ 4(1-/?) >6.

Предполагая, что смешанная стратегия pa + (1 — р)с может строго доминировать чистую стратегию Ь, также получим невыполнимое неравенство 2/?+ 4(1-/?) >8.

Следовательно, в данной игре не существует строго доминируемых стратегий первого игрока.

Рассмотрим стратегии второго игрока. Выпишем матрицу его выигрышей:

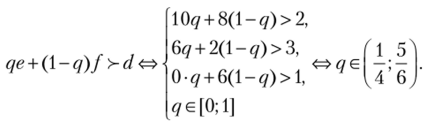
Очевидно, стратегии ей/ недоминируемы. Поскольку 2 < 8, 2 < 10, 3 е [2; 6], 1 е [0; 6], то можем предположить, что существует смешанная стратегия qe + (l-q)f, строго доминирующая чистую стратегию d. Проверим наше предположение. Для этого требуется выполнение системы неравенств:

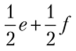
Необязательно было решать систему неравенств. Достаточно догадаться, что эта система имеет какое-нибудь решение. Например, в данной задаче видно, что смешанная стратегия строго доминирует стратегию d.

Важно понимать, что не только второй игрок исключает стратегию d, но и первый игрок, поставив себя на место второго и выполнив за него все указанные операции, может прийти к вывод}' об исключении стратегии d.

Вычеркнув первый столбец, получим матрицу.

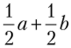
Нетрудно увидеть, что в этой матрице смешанная стратегия первого игрока строго доминирует стратегию с (это стало очевидным только после исключения стратегии d). Игра сократилась до биматричной игры размерности 2×2:

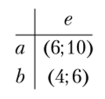aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Теперь е>/. Получим И наконец, а >- Ь.

Равновесие Нэша: (а; е). Этот исход будет единственным равновесием Нэша в исходной игре, поскольку процедура исключения строго доминируемых стратегий не может исключить равновесный по Нэшу профиль стратегий.

Пример 2.24. Последовательным исключением строго доминируемых чистых стратегий привести биматричную игру к игре размерности 2×2 (смешанная стратегия может доминировать чистую). Найти все равновесия Нэша в смешанных стратегиях.

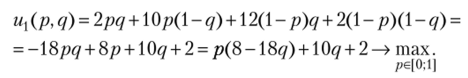
5) Пусть первый игрок играет смешанную стратегию рА + ( 1 — р)С, а второй — qE + (-q)F.

Выигрыш первого игрока равен.

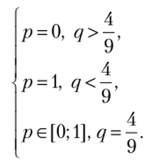
Из условия максимизации функции выигрыша по переменной р получим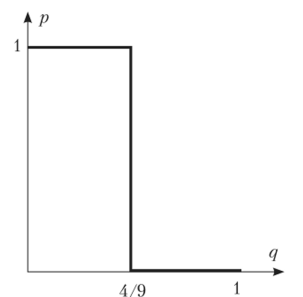

Графически этот выбор изображается следующим образом (рис. 2.32).

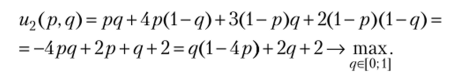
Рис. 2.32.

Это наилучшее для первого игрока действие, зависящее от выбора вероятности q вторым игроком.

Выигрыш второго игрока равен.

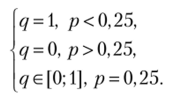
Из условия максимизации функции выигрыша по переменной q получим 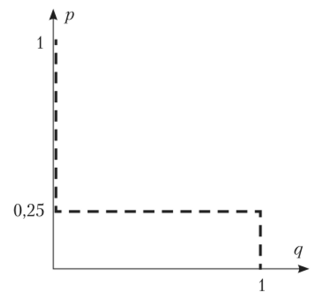Графически этот выбор изображается следующим образом (рис. 2.33).

Рис. 2.33.

Совместим графики на рис. 2.32 и 2.33 (рис. 2.34).

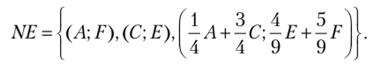
Рис. 2.34.

Графики совпадают в трех точках. Эти точки и будут определять равновесия Нэша:

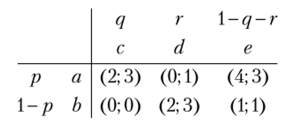
Пример 2.25. Найти все равновесия Нэша в смешанных стратегиях в биматричной игре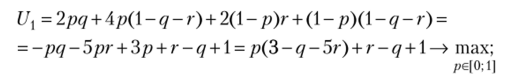

Решение

Способ 1. Нетрудно видеть, что в данной игре не существует строго доминируемых стратегий. Введем смешанные стратегии игроков:

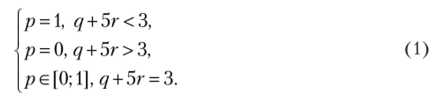
Выигрыш первого игрока максимизируем по переменной р: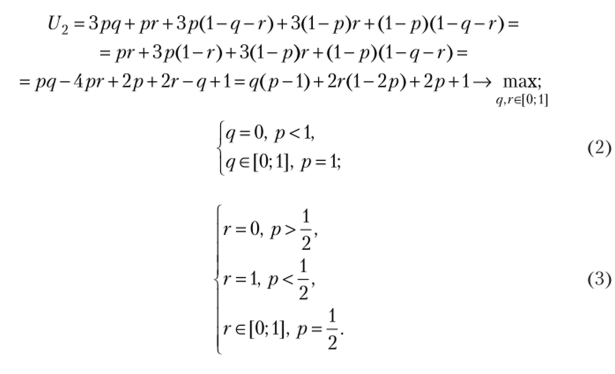

Выигрыш второго игрока максимизируем по переменным q и г.

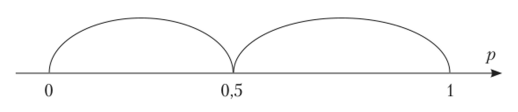
Рассмотрим различные значения р (рис. 2.35).

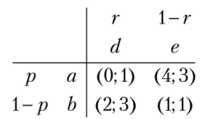
Рис. 235.

Случай 1. Пусть р < 0,5. Тогда из (2) и (3) получим <7 = 0; r= 1. Но тогда из (1) имеем р — 0. Итак, (р = ();q = 0;г = 1) — равновесие Нэша. Это исход (b, d).

Случай 2. Пусть р = 0,5. Тогда из (2) получим q = 0, а из (1) 5г= 3, или г = 0,6. Следовательно, (р = 0,5; q = 0; г = 0,6) — равновесие Нэша. Это исход (0,5а + 0,56, 0,6d + 0,4е).

Случай 3. Пусть р е (0,5; 1). Тогда из (2) и (3) получим q = 0; г= 0. Но тогда из (1) имеем р = 1, что противоречит исходному условию.

Случай 4. Пусть р = 1. Тогда из (3) получим г = 0, а из (1) q< 3, что выполняется при всех допустимых q. Итак, (р = 1; (a, qc + (-q)e), qe[ 0; 1].

Ответ: (6, d) (0,5а + 0,56, 0,6с/ + 0,4с); (a, qc + (-q)e), ^е[0;1].

Покажем еще один способ нахождения равновесий Нэша в таких играх.

Способ 2 (решения примера 2.25). Рассмотрим выигрыши второго игрока при условии выбора первым игроком смешанной стратегии ра + (-р)Ь. Выигрыш второго игрока при выборе им чистой стратегии с равен U - 3 р при выборе чистой стратегии d — = р + 3(- р)] при выборе чистой стратегии е — U?₂ =Зр + (-р).

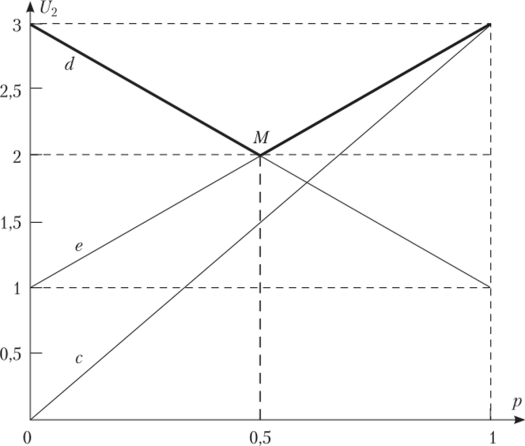
Построим графики функций выигрыша второго игрока (рис. 2.36).

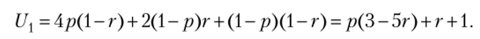
Рис. 2.36.

Случай 1. Пусть р < 0,5. Тогда второй игрок выбирает чистую стратегию d. Но наилучшим ответом первого игрока на стратегию второго d является чистая стратегия b (2 > 0), т. е. р- 0, что удовлетворяет исходному условию р< 0,5. Следовательно, (b, d) — равновесие Нэша.

Случай 2. Пусть р е (0,5; 1). Тогда второй игрок выбирает чистую стратегию е. Но наилучшим ответом первого игрока на стратегию второго е является чистая стратегия а (4 > 1), т. е. р = 1, что не удовлетворяет исходному условию. В данном промежутке нет равновесий Нэша.

Случай 3. Пусть р = 0.5. Тогда вторым игроком не будет играться стратегия с, г. е. q — 0. Рассмотрим игру.

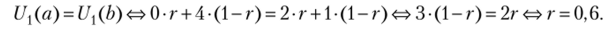
Математическое ожидание выигрыша первого игрока равно.

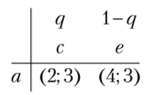
Значение р = 0,5 может быть наилучшим ответом на смешанную стратегию второго игрока только при г = 0,6. Тогда исход (0,5а + 0,56, 0,6d + + 0,4с) — равновесие Нэша.

К тому же результату мы придем и из других рассуждений. А именно, для первого игрока значение р = 0,5 возможно только в случае его безразличия к выбору стратегии, а или Ь. Э го значит: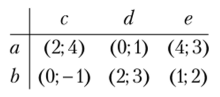

Случай 4. Пусть р= 1. Тогда вторым игроком не будет играться стратегия d, т. е. г = 0. Матрица принимает вид.

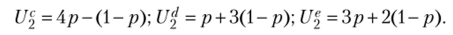
Тогда (a, qc + (1 — q)e) — равновесие Нэша при любых <�у е 10; 1 ].

Пример 2.26. Найти все равновесия Нэша в смешанных стратегиях в биматричной игре.

Решение.

Рассмотрим выигрыши второго игрока при использовании им чистых стратегий в ответ на смешанную стратегию первого игрока:

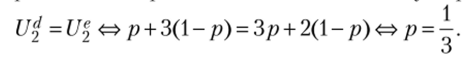
Построим графики этих функций (рис. 2.37).

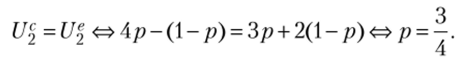
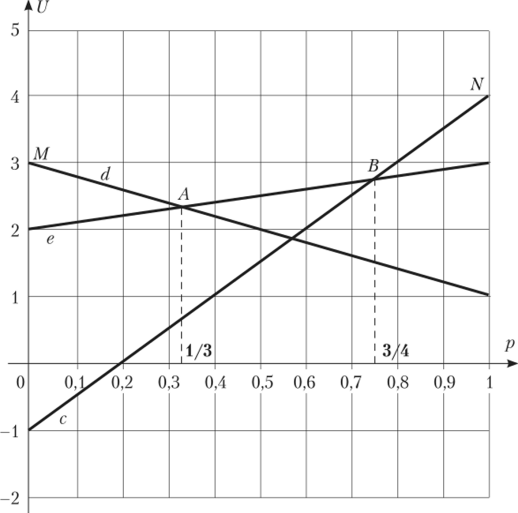
Рис. 2.37.

В точке А пересекаются прямые d не. Найдем точку пересечения:

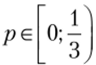
В точке В пересекаются прямые сие. Найдем точку пересечения:

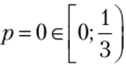
Ломаная линия MABN — наилучший ответ второго игрока при различных значениях р. Рассмотрим несколько случаев.

Случай 1: 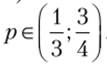. Тогда наилучшим ответом второго игрока является чистая стратегия d. Но наилучшим ответом первого игрока на чистую стратегию d второго игрока является чистая стратегия й, что соответствует значению 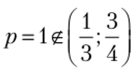. В этом промежутке получили единственное равновесие Нэша (b, d).

Случай 2: 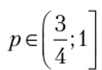. Тогда наилучшим ответом второго игрока является чистая стратегия е. Но наилучшим ответом первого игрока на чистую стратегию е второго игрока является чистая стратегия а, что соответствует значению 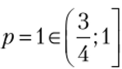. В этом промежутке нет равновесий Нэша.

Случай 3: 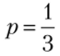. Тогда наилучшим ответом второго игрока является чистая стратегия с. Но наилучшим ответом первого игрока на чистую стратегию с второго игрока является чистая стратегия а, что соответствует значению 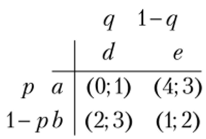. В этом промежутке получили единственное равновесие Нэша (а_} с).

Случай 4: 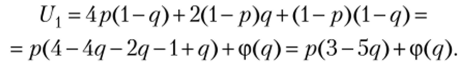(точка Л). В этой точке заведомо не играется стратегия с. Матрица игры принимает вид.

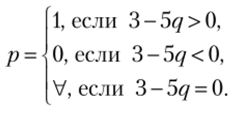
Рассмотрим математическое ожидание выигрыша первого игрока: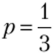

При равновесном по Нэшу исходе первый игрок максимизирует по р свою функцию полезности:

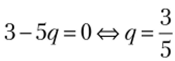
Очевидно, если 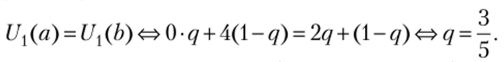является оптимальным для первого игрока, то.

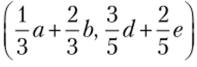. Это значение можно получить из условия равенства значений функции выигрыша первого игрока при выборе им а и /;. Иными словами, первому игроку безразлично, выберет он а или b:

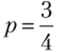aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">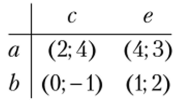

Следовательно, профиль стратегий является равно.

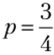
весием Нэша.

Случай 5: (точка В). В этой точке заведомо не играется стратегия d. Матрица игры принимает вид.

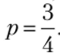
Поскольку а >- b, то р = 1, что противоречит исходному условию 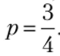Следовательно, не существует равновесия Нэша, при котором второй игрок выбирает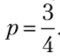

Этот метод решения можно применять для нахождения равновесий Нэша в любых биматричных играх размерности 2 хп или п х 2, и, следовательно, он более универсален, чем метод, примененный в способе 1 решения предыдущего примера.

• [1] Здесь и далее в аналогичных примерах стратегии Саши (Футбол, Балет) обозначенысловом, начинающимся с заглавной буквы, стратегии Маши — со строчной.