Теорема Чебышева. 
Теория вероятностей

Теорема Чебышева. Если дисперсии п независимых случайных величин Х_{, Х₂, Х" ограничены одной и той же постоянной, то при неограниченном увеличении числа п средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий а₂, …, а,_р т. е.

или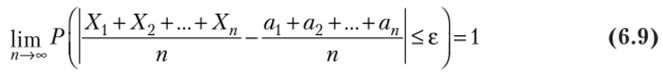

? Вначале докажем формулу (6.9), затем выясним смысл формулировки «сходимость по вероятности». По условию.

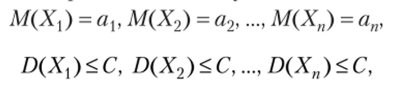
где С — постоянное число.

Получим неравенство Чебышева в форме (6.6) для средней арифметической случайных величин, т. е. для.

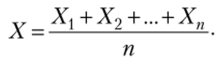
Найдем математическое ожидание М (Х) и оценку дисперсии О (Х):

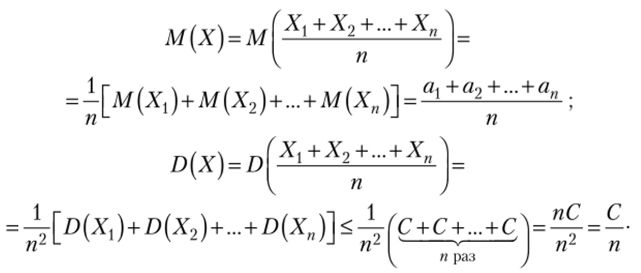
(Здесь использованы свойства математического ожидания и дисперсии и, в частности, то, что случайные величины Х_1у Х₂,Х_п независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.).

Запишем неравенство (6.6) для случайной величины X = (Х₁ + + Х₂+ …+ Х") / п:

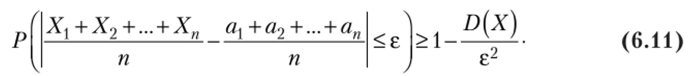
Так как по доказанному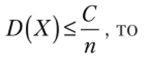

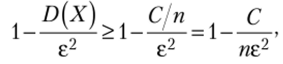
и от неравенства (6.11) перейдем к более сильному неравенству: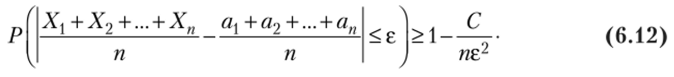

п ^с

В пределе при п —> оо величина —- стремится к нулю, и получим доказываемую формулу (6.9).? ^т

Выясним теперь смысл формулировки «сходимость по вероятности» и записи ее содержания в виде (6.10). Понятие предела переменной величины 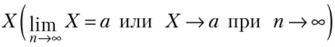означает, что начиная с некоторого момента ее изменения для любого (даже сколь угодно малого) числа е>0 будет верно неравенство |Х-а| [1]

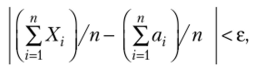
где 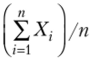 — случайная величина, а  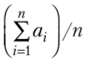— постоянное число.

Однако из неравенства (6.9) вовсе не следует, что оно будет выполняться всегда, начиная с некоторого момента изменения 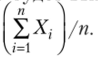Так как  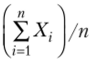— случайная величина, то возможно, что в отдельных случаях неравенство выполнятьсяне будет. Однако с увеличением числа п вероятность неравенства 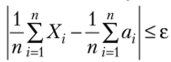стремится к 1, т. е. это неравенство будет выполняться в подавляющем числе случаев. Другими словами, при достаточно больших п выполнение рассматриваемого неравенства является событием практически достоверным, а неравенства противоположного смысла — практически невозможным.

Таким образом, стремление 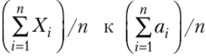следует понимать не как категорическое утверждение, а как утверждение, верность которого гарантируется с вероятностью, сколь угодно близкой к 1 при п —> оо. Это обстоятельство и отражено в формулировкетеоремы «сходится, но вероятности» и в записи (6.10) обозначением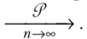

Подчеркнем с м ы с л теоремы Чебышева. При большом числе п случайных величин Х_х, Х₂, …" Х_п практически достоверно, что их средняя.

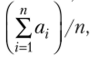
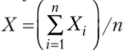 — величина случайная, как угодно мало отличается от неслучайной величины т. е. практически перестает быть случайной.

Следствие. Если независимые случайные величины Х_х, Х₂, …, Х_п имеют одинаковые математические ожидания, равные а, а их дисперсии ограничеиы одной и той же постоянной, то неравенство (6.12) и формулы (6.9), (6.10) примут вид

или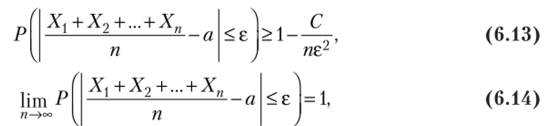

? Формулы (6.13)—(6.15) следуют из формул (6.12), (6.9) и (6.10),.

так как.

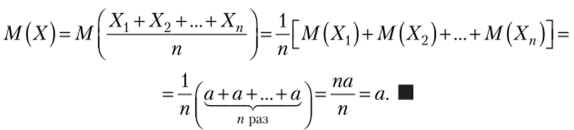
Теорема Чебышева и ее следствие имеют большое практическое значение. Например, страховой компании необходимо установить размер страхового взноса, который должен уплачивать страхователь; при этом страховая компания обязуется выплатить при наступлении страхового случая определенную страховую сумму. Рассматривая частоту/убытки страхователя при наступлении страхового случая как величину случайную и обладая известной статистикой таких случаев, можно определить среднее число/ средние убытки при наступлении страховых случаев, которое на основании теоремы Чебышева с большой степенью уверенности можно считать величиной почти не случайной. Тогда на основании этих данных и предполагаемой страховой суммы определяется размер страхового взноса. Без учета действия закона больших чисел (теоремы Чебышева) возможны существенные убытки страховой компании (при занижении размера страхового взноса) либо потеря привлекательности страховых услуг (при завышении размера взноса).

Заметим, что разработкой математических методов и моделей, применяемых в страховании, занимается так называемая актуарная (страховая) математика.

Другой пример. Если надо измерить некоторую величину, истинное значение которой равно а, проводят п независимых измерений этой величины. Пусть результат каждого измерения — случайная величина X, (г = 1, 2,…, п). Если при измерениях отсутствуют систематические погрешности (искажающие результат измерения в одну и ту же сторону), то естественно предположить, что М (Х,) = а при любом г. Тогда на основании следствия из теоремы Чебышева средняя арифметическая результатов п измерений 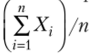сходится по вероятности к истинному значению а. Этим обосновывается выбор средней арифметической в качестве меры истинного значения а.

Если все измерения проводятся с одинаковой точностью, характеризуемой дисперсией Д (Х_;) =о², то дисперсия их средней.

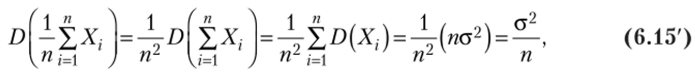
а ее среднее квадратическое отклонение равно 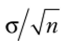. Полученное отношение, известное под названием «правила корня из п»_у говорит о том, что средний ожидаемый разброс средней п измерений в 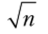раз меньше разброса каждого измерения. Таким образом, увеличивая число измерений, можно как угодно уменьшать влияние случайных погрешностей (но не систематических), т. е. увеличивать точность определения истинного значения а.

Замечание. Если измерительный прибор имеет точность 5 (например, 8 — половина ширины деления равномерной шкалы прибора, по которой производится отсчет), то указанным выше способом нельзя рассчитывать получить точность измерения величины а большую, чем б. Каждое измерение дает результат с неопределенностью 5 и, очевидно, их средняя арифметическая будет обладать той же неопределенностью 5. Таким образом, стремиться посредством закона больших чисел получить значение а с большей степенью точности, чем позволяет прибор при отдельном измерении, является заблуждением.

Точно так же, как увеличение числа независимых измерений неизвестной величины в соответствии с формулой (6.15') приводит к уменьшению получаемой ошибки, увеличение числа проводимых (не связанных друг с другом) финансовых операций на рынке при той же доходности приводит к снижению риска^[2]. Эго связано с тем, что убытки от одних операций более или менее покрываются прибылью от других операций. Отсюда следует один из принципов работы на финансовом рынке, известный как принцип диверсификации (разнообразия) и вполне согласующийся с народной мудростью: «не клади все яйца в одну корзину».

О Пример 6.7. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения ламп во всей партии не более чем на 5 ч (по абсолютной величине), если известно, что среднее квадратическое отклонение продолжительности горения ламп в каждом ящике меньше 7 ч.

Решение. Пусть X, — продолжительность горения электролампы, взятой из г-го ящика (ч). По условию дисперсия ?)(Х_/)<7²= 49. Очевидно, что средняя продолжительность горения отобранных ламп равна (Х_х + Х₂ +…+ Х_2(ю)/200, а средняя продолжительность горения ламп во всей партии (М (Х_{) + М (Х₂) +…+М (Х₂₀₀))/200 = (а_х + а₂ + … + «₂₀₀)/200.

Тогда вероятность искомого события по формуле (6.12):

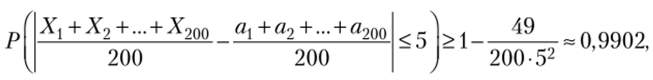
т.е. н е м е н е е чем 0,9902. ?

[> Пример 6.8. Сколько надо провести измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 1 (по абсолютной величине), если среднее квадратическое отклонение каждого из измерений не превосходит 5?

Решение. Пусть X, — результат ?-го измерения (/ = 1, 2,…, п); а — истинное значение величины, т. е. М (Х,) = а при любом ?.

Необходимо найти п, при котором.

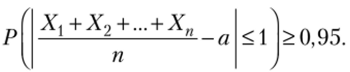
В соответствии с неравенством (6.12) данное неравенство будет выполняться, если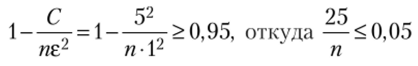

и 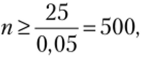т. е. потребуется не менее 500 измерений. ?

• [1] Записываем его кратко с помощью знаков суммирования.
• [2] Напомним (см. параграф 3.4), что под риском данной финансовой операции здесьпонимается дисперсия или среднее квадратическое отклонение ее доходности.