Особенности обработки экспериментальных результатов и примеры использования методики контроля параметров капсюлей электретных преобразователей

Значительно уменьшающий ЭП в воздушном зазоре, прогиб мембраны уменьшается (уо < 8 л/ли/, табл. 2.4.3) и дефект перестает на неё влиять. При этом наблюдается хорошее соответствие расчётной и экспериментальной кривых С, (UJ рис. 2.4.5 (особенно в квадратичном приближении). Следует отметить, что отличие расчётных и экспериментальных результатов может быть объяснено и другими причинами, например… Читать ещё >
Особенности обработки экспериментальных результатов и примеры использования методики контроля параметров капсюлей электретных преобразователей (реферат, курсовая, диплом, контрольная)
Как уже указывалось, при обработке экспериментальных значений C/UJ во внимание должны быть приняты только С,, не превышающие 1,5 Со. Это связано с тем, что согласно рассматриваемой методике значения С, > 1,5 Со соответствуют залипанию мембраны. Поэтому С" наблюдаемые в этом случае, нс соответствуют разработанной модели, а связаны с наличием инородных включений в воздушном зазоре, различных неровностей и других причин, препятствующих залипанию. Поэтому, в частности, если в эксперименте нс наблюдается скачкообразного роста С, после С, = 1,5 Со, то можно сделать вывод о невысоком качестве преобразователя.
Другой важной особенностью обработки экспериментальных данных является то, что из расчетов должны быть исключены значения С" измеренные при U = -Uj и близким к — U-) значениям напряжения. Это связано с тем, что в расчётных формулах.
(например, (2.1.11) при U = -Uj получается неопределенность вида jj-. Поэтому рассматривать следует значения С, надёжно отличающиеся от Со.
Принятые во внимание значения С, и U, вводятся в разработанною программу (см. ниже), по которой производится расчет параметров (dj, г и др.) электретной КСПО и осуществляется проверка результатов расчёта. Полученные значения г, подлежат статистической обработке. Наиболее простая статистическая обработка основана на классической теории ошибок При этом среднее значение натяжения.

где п — число измерений, а средняя ошибка среднего арифметического где п — число измерений, а средняя ошибка среднего арифметического.
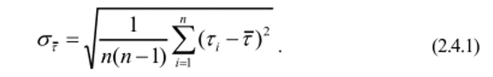
Известно, что, например, с вероятностью Р = 96% можно утверждать, что истинное значение г находится в интервале т ~ 2ст- 4- г 4- 2(7-.
В таблице 2.4.1 сведены результаты измерений и расчётов, связанных с исследованием капсюля одной из модификаций электретного микрофона МКЭ-100. Экран был подсоединен к точке 1, рис. 2.2.1. В табл. 2.4.1 выделены те значения С, и Ut, которые были приняты в рассмотрение в связи с замечаниями, указанными выше. На рис. 2.4.1 показаны экспериментальные и расчётные зависимости Q (U).
На рис. 2.4.2 показан разброс расчётных значений и при использовании различных способов расчёта, из которого, в частности, видно, что отчётливой корреляции между т и у0 нет. Это свидетельствует о том, что натяжение мембраны существенно не возрастает при сс прогибе. Из данных табл.2.4.1 видно, что относительная погрешность по разбросу при определении г составляет около 12% (уровень доверительной вероятности Р=96%).
В табл. 2.4.2 и на рис. 2.4.3 и 2.4.4 приведены аналогичные результаты исследования того же капсюля микрофона МКЭ-100, отличающиеся от предыдущих только тем, что в процессе измерений экран был подсоединен к точке 3, рис. 2.2.1. Соответственно, в расчётах использовалось другое значение Си, табл. 2.4.2.
Из данных табл. 2.4.2 видно, что при том же уровне доверительной вероятности относительная погрешность по разбросу при определении г составляет около 8% (поршневое приближение) и 6% (квадратичное приближение). Таким образом, использование подсоединения экрана к точке 3, рис. 2.2.1, позволило в данном случае существенно улучшить точность определения т. Кроме того, из рис. 2.4.3 видно, что в данном случае расчётные кривые лучше соответствуют эксперименту, чем в случае, показанном на рис. 2.4.1. Видно также, что и рассчитанная в квадратичном приближении кривая С, (UJ лучше соответствует эксперименту, чем расчётная кривая С/ (Vi), полученная в поршневом приближении. Вместе с тем, следует отметить, «гто во всех случаях получено достаточно хорошее соответствие экспериментальных и расчётных данных. Результаты расчёта в поршневом и квадратичном приближениях в данном случае не очень сильно различаются. Вероятно, это связано с тем, что для имевшегося в нашем распоряжении исследованного микрофона а ~ /?, поэтому введенный в п. 2.1. коэффициент а ' не сильно отличается от своего истинного значения (0.5) в этом случае.
Таблица 2.4.1.
Результаты исследования капсюля микрофона МКЭ-100. Экран подсоединён к точке I (рис. 4.2.2.1).
иэ = -72 В (компенсационный метод); 11э = -73 В (из графика C,(Ut)): di = 32,5 лис и; </" = 6 лисы; А = 77,5 м/см;
а = 5,4.ми; ft = 6лш;С = 4825 пФ; Спи = 12.6 пФ, СПЛ = 18.9 иФ; Суии = 1,5 лФ =2,2.
ил | — 70 -60 -50 -40. | — 30 -20 -10 0 25. | 50 75 100. | 125 150 175. | 200 225. | |
Сх.пФ | 80,0 74,8 71,2 68,0. | 59,4 58,5 57,8 57,2 56,6. | 50,0 55,7 56,0. | 56,3 57,3 58,7. | 69,7 79,4. | |
G, л Ф | 48,0 42,6 38,9 35,6. | 26,9 25,9 25,2 24,6 24,0. | 29,4 23,1 23,4. | 23,7 24,7 26,1. | 37,4 47,9. | |
1 |f'=26-8^ 1* = ,'8^7. | Топ. мкм | 30,9 27,3 24,2 21,0. | 8,59 6,63 5,17 3,85 2,47. | 1,01 0,256 1,01. | 1,75 4,08 7,04. | 22,9 30,4. |
г, Н/м | 52,0 40,1 32,1 26,2. | 30,3 29,6 28,5 28,1 17,8. | 9,04 0,646 14,6. | 31,2 31,5 35,5. | 34,7 59,5. | |
fc 1 г2 «26.8 — а. ё ' •» з ю «. я s, _ п СО ГУ <7 г —1,7; 14 П • -«. | У02 «мкм | 26,4 24,0 21,8 19,3. | 8,36 6,52 5,12 3,84 2,48. | 1,04 0,280 1,04. | 1,76 4,08 6,86. | 20,2 26,2. |
г, Н/м | 59,1 43,5 33,7 26,6. | 28,4 27,4 26,3 25,7 16,4. | 8,01 0,539 13,0. | 28,2 28,6 33,1. | 35,9 67,3. | |
. *. X х. II — = &г = г! | уЗ. мкм | 10,8. | 7,35 5,90 4,43 3,27 1,30. |
| 1,67 3,93 8,03. | ; |
/-?0) S3 «. пФ | 28,4. | 26,6 25,6 24,9 24,4 23,5. | 23,1 23,0 23,2. | 23,7 24,7 26,7. | ||
g 1.
| Ум > лкм. | 13,9. | 9,21 6,75 5,01 3,67 1,44. |
| 1,86 4,43 9,52. | ; |
30,6. | 27,4 26,1 25,2 24,6 23,6. | 23,1 23,0 23,2. | 23,8 24,9 27,6. | ; | ||
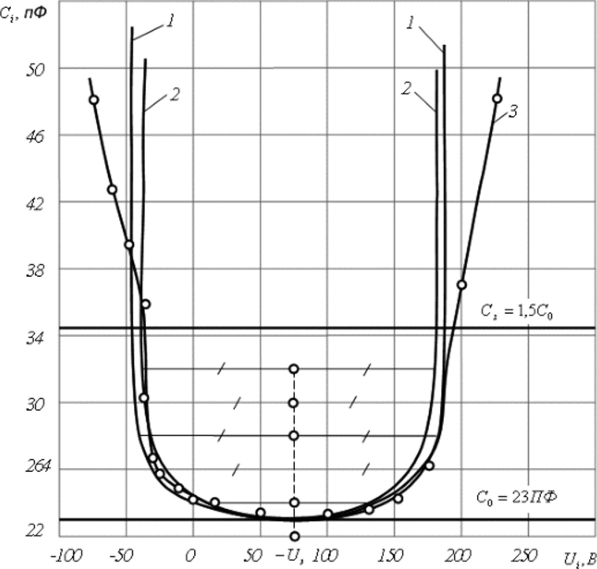
Рис. 2.4.1. Экспериментальные и расчетные зависимости C,(Ui) для капсюля микрофона МКЭ-100. Экран — на точке 1 (рис. 42.2.1). 1,2- расчетные кривые, 3 — эксперимент;! G (Ui) при г = г, (поршневое приближение), 2 — C,(Ui) при г = г, (квадратичное приближение).
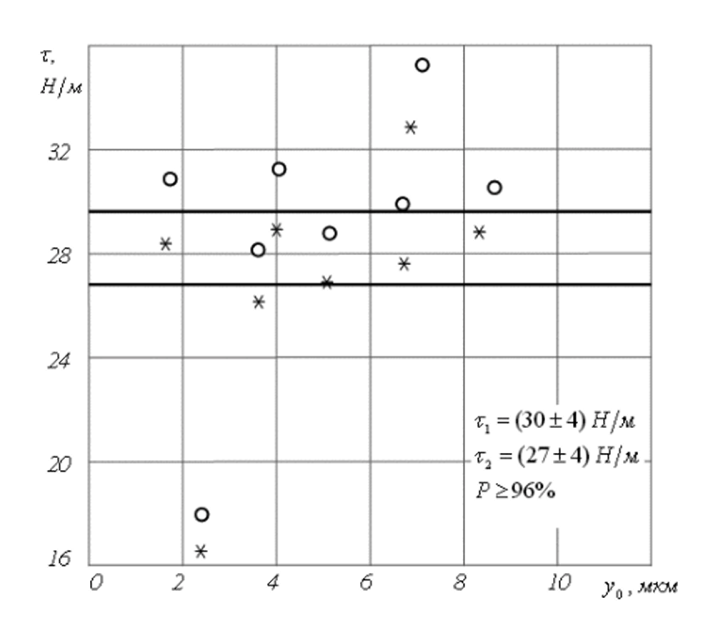
Рис. 2.4.2. Расчетные значения натяжения мембраны капсюля МЮ-100. Экран — на точке 1 (рис. 2.2.1)о — расчет в поршневом приближении;* - расчет в квадратичном приближении; прямые — средние значения; г, — расчет в поршневом приближении; г, — расчет в квадратичном приближении.
Таблица 2.4.2.
Результаты исследования капсюля микрофона МКЭ-100. Экран подсоединён к точке 3 (рис. 2.2.1).
V) = -72 В (компенсационный метод); di = 32,1 лиси; d’г — биоси; А = 76,6 и оси; а = 5,4 .им; Ь = 6 мм с" =22.
1/э = -72 В (из графика CtfUi)) = 6 леи; О = 4825 лФ; См = 21,5 лФ; Си". = 18.9 лФ; Сюот= 1,5 лФ.
UJd | — 50. | ^0. | — 30. | — 20. | — 10. | |||||||||
Сх, п Ф | 89,54. | 79,80. | 71,38. | 69,72. | 68,32. | 66,75. | 65,56. | 64,98. | 64,82. | 65,12. | 65,95. | 67,58. | 71,10. | |
С/, п Ф | 48,61. | 38,61. | 30,00. | 28,31. | 26,88. | 25,28. | 24,07. | 23,48. | 23,62. | 24,46. | 26,12. | 29,72. | ||
?2 Г = 23.4 —. | Уоп ЛЮ/. | 30,4. | 2Ъ2 | 13,1. | 10,3. | 7,79. | 4,58. | 1,87. | 0,448. | 0,025. | 0"792. | 2,77. | 6,31. | 12,6. |
||ст, =,.ос" . С = «. | г, н/м | 39,9. | 27,9. | 24,8. | 22,6. | 21,6. | 25,0. | 23,6. | 20,6. | 6,73. | 19,1. | 20,94. | 22,7. | 25,6. |
s Sf==2l-8T. | У02″ ЛЛСИ. | 26,1. | 21,0. | 12,5. | 10,0. | 7,64. | 4,52. | 1,88. | 0,480. | 0,024. | 0,800. | 2,76. | 6,20. | 12,1. |
J |<�гг— = 0,651 | . г2, Н/м | 45,3. | 29,0. | 23,8. | 21,4. | 20,1. | 23,0. | 21,4. | 17,5. | 6,40. | 17,2. | 19,1. | 21,1. | 24,5. |
Щ 1. 1!г=г- | Ую, -V//CV/. | ; | ; | 13,0. | 8,58. | 6,16. | 4,44. | 1,71. | 0,357. | 0,066. | 0,583. | 2,21. | 5,41. | 13,9. |
с, н/м | ; | ; | 30,4. | 27,4. | 26,1. | 25,2. | 24,0. | 23,4. | 23,3. | 23,5. | 24,2. | 25,7. | 31,1. | |
ё 1. | у;?" л*си. | ; | ; | ; | 9,64. | 6,76. | 4,82. | 1,84. | 0,383. | 0,007. | 0,625. | 2,39. | 5,91. | 16,9. |
3 ю _. I I г = г2 | 42)" ЯД/. | ; | ; | ; | 28,1. | 26,4. | 25.4. | 24,0. | 23,4. | 23,3. | 23,5. | 24,3. | 25,9. | 53,7. |
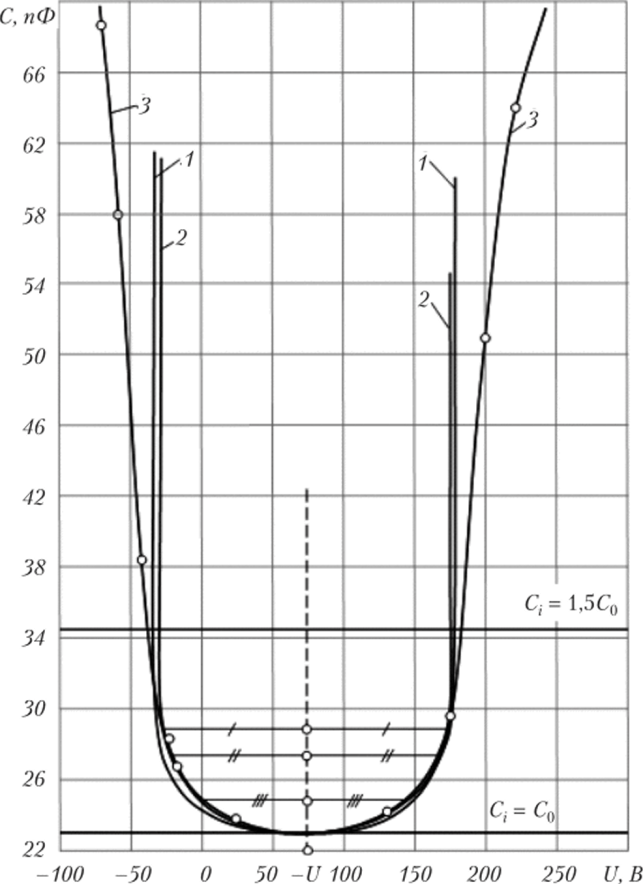
Рис. 2.4.3. Зависимость С, (U,) для капсюля МКЭ-100. Экран — на точке 3 (рис. 2.2.1).
1-расчет С,(С/,) при г = г, (поршневое приближение), 2-расчет C,(Ut) при г = F, при (квадратичное приближение), 3 — эксперимент.
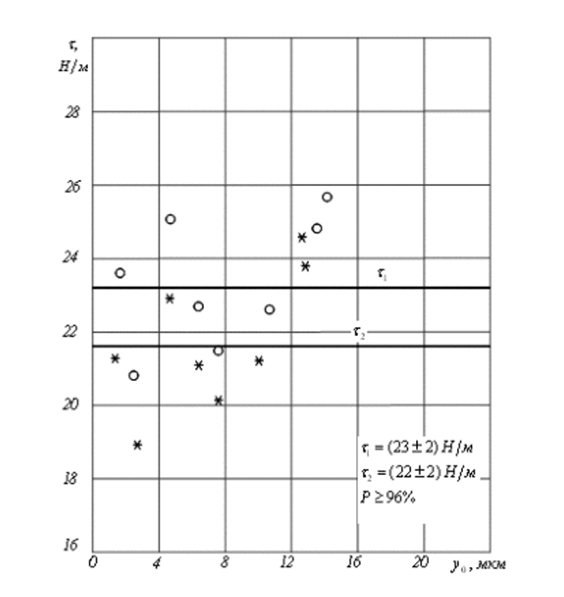
Рис. 2.4.4. Расчетные значения натяжения мембраны капсюля микрофона МКЭ-100. Экран — на точке 3 (рис. 2.2.1).о — расчет в поршневом приближении;* - расчет в квадратичном приближении; прямые — средние значения (г, — поршневое приближение, г, — квадратичное приближение).
Очевидно, при а «Ь коэффициент а тоже не сильно отличается от своего истинного значения а «1. Поэтому погрешность поршневого приближения максимальна при а ~ Ь/2. Для проверки этого предположения был изготовлен лабораторный макет электретного преобразователя. Результаты его исследования сведены в табл. 2.4.3 и показаны на рис. 2.4.5 и 2.4.6.
Видно, что в данном случае использование квадратичного приближения дает результаты расчёта значительно лучше соответствующие эксперименту, чем при использовании поршневого приближения. Кроме того, в отличие от капсюля микрофона МКЭ-100, значения г/ и г.?, рассчитанные соответственно в поршневом и квадратичном приближениях, различаются существенно. 1 1аконец, напомним, что по виду экспериментальной кривой С, (U) и точности её соответствия расчёту можно судить о качестве капсюля преобразователя. В целом, это соответствие в данном случае хуже, чем у капсюля МКЭ-100: экспериментальная кривая С, (У<) не гладкая (как в случае МКЭ-100), имеет изломы, которые можно объяснить наличием неровностей и инородных включений в воздушном зазоре и неравномерным по площади натяжением мембраны; кривая С, (UJ после достижения значения 0=1,5С" продолжает возрастать плавно, в то время как, согласно разработанной модели, должно произойти скачкообразное возрастание О • Это отклонение объясняется уже рассмотренными выше причинами.
Для проверки разработанной модели и выявления качества исследованных капсюлей представляет интерес также сравнить расчётные и экспериментальные значения напряжения залипания мембран (экспериментальные значения U, определялись по резкому увеличению С, при увеличении U, на небольшую величину AU). Результаты приведены в табл. 2.4.4, составленной на основе полученных выше выражений (2.3.7) (поршневое приближение) и (2.3.8) (квадратичное приближение). Отмстим, что как видно из вольт-фарадных характеристик и указанных выражений, этих значения два. Эти пары значений и приведены в табл. 2.4.4.
Видно, что для МКЭ-100 расчётные и экспериментальные значения U, удовлетворительно соответствуют друг другу. Те обстоятельства, что: 1) экспериментальные значения по величине несколько больше расчётных и 2) расчёт в поршневом приближении может лучше соответствовав эксперименту, чем расчёт в квадратичном приближении (а не наоборот) объясняются тем, что при значительном прогибе центра мембраны (когда U—>U) становятся существенными шероховатости электрода и мембраны, их волнистость, наличие пылинок, препятствующих залипанию и т. д.
Таблица 2.4.3.
Результаты исследований лабораторного тлектретного преобразователя. Экран — на точке 3 (рис. 3.4). 66 ~ -2005 (компенсационный метод). 16=-197/?(из минимума вольт-фарадной характеристики)) di — 1462. мк"г, d: = 15. мюг; А = 336,7мкм: С*<=25пФ, йг=19,8л1Ц 6=35 .wr, С=4825лФ, G,=6,8/i0, Gui= $пФ
ЦВ | — 40. | — 30. | — 20. | — 10. | |||||||||||||
G. /7 Ф. | 99,7. | 99,8. | |||||||||||||||
С/, пФ | 96,2. | 81,3. | 77,9. | 74,6. | 72,5. | 71,9. | 71,3. | 71,2. | 71,2. | 71,9. | 74,4. | ||||||
^-24,2 «. g 1. " 1,03 — С п Л". | Том ЛШ1 | 93,8. | 39,2. | 31,2. | 76,2. | 63,7. | 47,4. | 22,7. | 15,7. | 1,78. | 0,15. | ; | 0,15. | 1,77. | 7,80. | ||
Г, Н/м | 44,4. | 38,7. | 32,9. | 23,0. | 25,2. | 20,1. | 22,0. | 20,3. | 22,5. | 29,9. | 24,4. | 69,3. | ; | 69,3. | 24,4. | 23,8. | |
н я За" =0.81 — Я с" -и. | У 02 У леем | 92,6. | 88,1. | 80,3. | 75,5. | 63,3. | 47,1. | 22,6. | 15,6. | 1,76. | 0,14. | ; | 0,14. | 1,78. | 7,82. | ||
г2, Н/м | 31,7. | 27,5. | 23,4. | 20,5. | 17,8. | 14,1. | 15,4. | 15,7. | 20,3. | 17,1. | 53,0. | ; | 53,0. | 17,0. | 16,5. | ||
= 1. ||Г = Г| | У%9 лаем | 48,0. | 37,9. | 31,8. | 27,1. | 18,7. | 12,8. | 8,43. | 2,85. | 0,31. | 0,31. | 1,24. | 5,20. | ||||
СЦ Н/м | ; | 96,9. | 90,1. | 83,7. | 79,4. | 76,6. | 74,4. | 72,4. | 71,7. | 71,4. | ; | 71,4. | 71,7. | 73,3. | |||
Ум «ЛКИ. | ; | ; | ; | ; | ; | 31,4. | 19,9. | 12,7. | 7,64. | 1,79. | 4,13. | 0,44. | ; | 0,44. | 1,79. | 7,64. | |
Квадрат. ириближ. II. J4'. | /-(2) '-'/з «. Н/м | ; | ; | ; | ; | ; | 86,1. | 80,0. | 76,6. | 74.4. | 72,9. | 71,9. | 71,4. | ; | 71,4. | 71,9. | 74,4. |
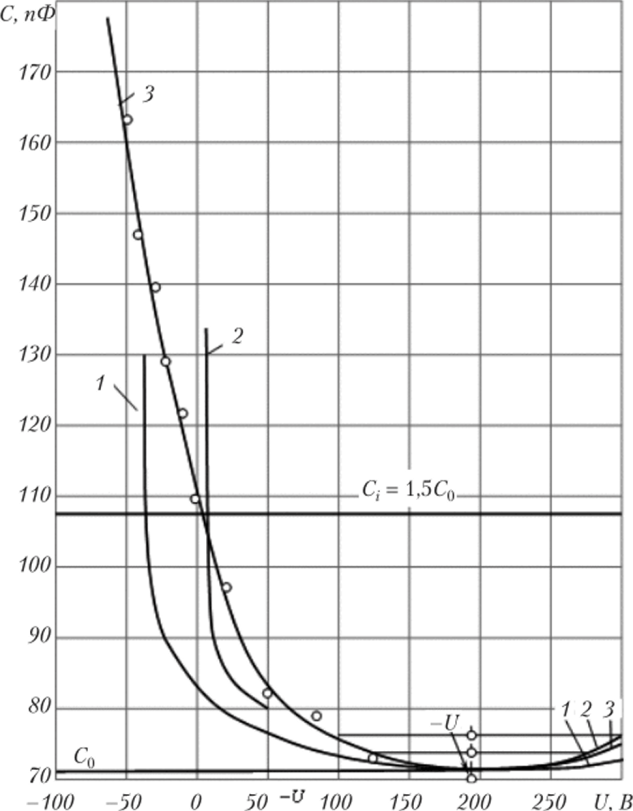
Рис. 2.4.5. Зависимость С, (?/,) для капсюля лабораторного образца электретного преобразователя. Экран — на точке 3 (рис. 2.2.1). 1 — расчет С, (V,) при г = г, (поршневое приближение), 2- расчет С., (?/,) при г = г, при (квадратичное приближение), 3 — эксперимент.
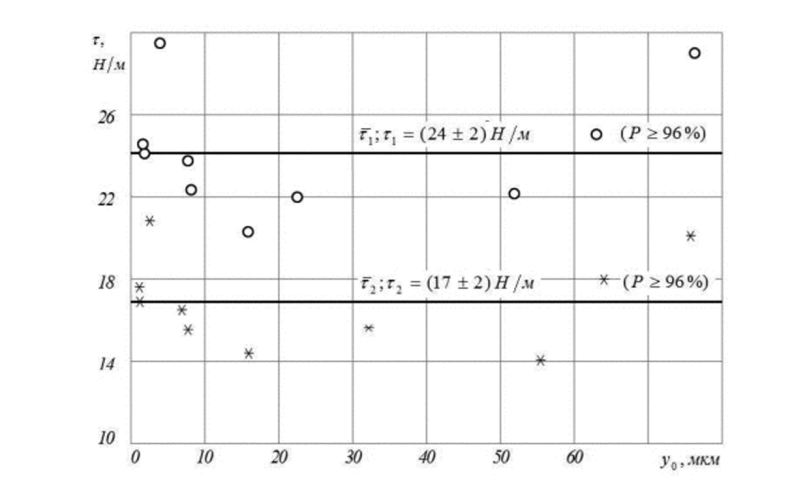
Рис. 2.4.6. Расчетные значения натяжения мембраны капсюля образца лабораторного электретного преобразователя. Экран — на точке 3 (рис. 3.4).о — расчет в поршневом приближении, * - расчет в квадрантном приближении; прямые — средние значения (г, — поршневое приближение, г, — квадратичное приближение).
Таблица 2.4.4.
Расчётные и экспериментальные значения (U+lfy, в Вольтах; г = г2.
Способ определения Капсюль. | Расчёт Ufa*l. | Эксперимент. Umn | |
поршневое приближение. | квадратичное приближение. | ||
МКЭ-100 без экрана. | — 41,3; 185. | — 39,7; 184. | — 39; 180. |
МКЭ-100 с экраном. | — 28,4; 172. | — 27,1; 171. | — 38; 180. |
Лабораторный, с экраном. | 61,1; 339. | 17,0; 383. | — 20; ; |
Поэтому экспериментально наблюдаемые U, по величине всегда должны быть больше расчетных. В то же время из изложенного ясно, что чем лучше в целом соответствие расчётных и экспериментальных значений U" тем выше качество преобразователя. Таким образом, использование метода вольт-фарадной характеристики позволяет не только неразрушающим способом контролировать параметры преобразователя, но и неразрушающим же способом контролировать наличие в нем дефектов — пылинок в рабочем зазоре, неплоскостность противоэлектрода и т. п. В этом отношении показателен испытанный лабораторный преобразователь низкого качества, у которого расчётные и экспериментальные значения U, заметно различаются. Правда, на фоне большого U, = -200 В это различие (37 В — в квадратичном приближении) не гак уж велико. Однако, само по себе заметное различие U3pacu и UiItn и тот факт, что оба расчётных значения U, (в том или ином приближении) имеют один знак, свидетельствует о том, что даже при U = 0 мембрана должна была бы залипнуть под действием одного только поля электрета. Отсутствие залипания можно объяснить только тем, что фактически при U= 0 мембране не дает залипнуть какой-то дефект (например, инородное включение в воздушном тюре) размером не менее.
d —у I О наличии этого дефекта свидетельствуют изломы на кривой С, (U) при U
' ''°и=0
= -80 100 В. Когда же на преобразователь подаётся потенциал U > 100 В,
значительно уменьшающий ЭП в воздушном зазоре, прогиб мембраны уменьшается (уо < 8 л/ли/, табл. 2.4.3) и дефект перестает на неё влиять. При этом наблюдается хорошее соответствие расчётной и экспериментальной кривых С, (UJ рис. 2.4.5 (особенно в квадратичном приближении). Следует отметить, что отличие расчётных и экспериментальных результатов может быть объяснено и другими причинами, например, неравномерным характером натяжения мембраны. Однако, в любом случае, по отклонению экспериментальных результатов от расчётных можно судить о том, что в преобразователе имеются отклонения от идеализированной конструкции, показанной на рис. 1.1.
Таким образом, разработанный метод является неразрушающим способом контроля и позволяет определять комплекс важнейших параметров электретных преобразователей непосредственно в конструкции их капсюлей по результатам одной операции — снятии вольт-фарадной характеристики. При этом не требуется специального оборудования, а схемотехническая реализация методики проста. Поэтому использование рассмотренного метода представляется перспективным при разработке и изготовлении новых электретных КСПО.