Виды текстовых задач в начальном математическом образовании

Вопросы для обсуждения.

• 1. Что дает учителю знание видов текстовых задач?
• 2. Почему учащимся необходимо умение решать простые задачи?
• 3. Можно ли утверждать, что принятые в методике тины простых задач исчерпывают все их многообразие?
• 4. Почему в методике выделяются виды задач по их сюжету?
• 5. Насколько важно научить детей решать задачи с пропорциональными величинами?
• 6. Какое значение в формировании умения решать задачи имеет включение нестандартных задач?

В методической науке выделены несколько видов (типов) текстовых задач. Все текстовые задачи подразделяются па простые — задачи, решаемые в одно действие, и составные — задачи, решаемые в два и более действий. Цель обучения решению простых задач рядом методистов трактуется как

средство усвоения детьми конкретного смысла каждого из арифметических действий^[1].

Простые задачи разбиты на несколько групп. Первая группа: задачи на нахождение суммы, остатка, суммы одинаковых слагаемых, деление на равные части, деление по содержанию. Например, задача «У Тани было пять конфет, две она съела. Сколько конфет осталось у Тани?» — задача на нахождение остатка.

Вторая группа включает задачи, решение которых вырабатывает усвоение связей между компонентами и результатами арифметических действий. Примером служит задача «После того как Таня съела две конфеты, у нее осталось три. Сколько конфет было у Тани первоначально?».

Третья группа включает задачи, решение которых способствует усвоению отношений: больше (меньше) на несколько единиц; больше (меньше) в несколько раз; разностного и кратного сравнения. Например, задача «В одной вазе пять ромашек, а в другой — на две ромашки меньше. Сколько ромашек в другой вазе?» относится к типу уменьшение числа на несколько единиц (прямая форма), и задача «В одной вазе пять ромашек, их на две больше, чем в другой. Сколько ромашек в другой вазе?» — также задача на уменьшение числа на несколько единиц (косвенная форма). В то же время задачу «В корзину с яблоками добавили шесть яблок. После того как несколько яблок взяли, в корзине осталось на два яблока меньше, чем было первоначально. Сколько яблок взяли?» трудно отнести к какому-нибудь из указанных типов, хотя она и решается в одно действие.

Это значит, что выделенные типы не являются классификацией в точном смысле этого слова, а это ведет к затруднениям детей при встрече с задачей незнакомого вида даже в том случае, если текст типовой задачи приведен не совсем в стандартной формулировке. Например, вместо привычной формы «За 2 ч пешеход прошел 10 км. Чему равна его средняя скорость?» (тип: деление на равные части) задача сформулирована в виде «Найдите скорость пешехода, если он за 2 ч удалился от начала пути на 10 км».

В то же время умение решать простые задачи полезно для овладения умениями решать любые задачи. Приведем пример работы над простой задачей, тип которой — «уменьшение числа в несколько раз в косвенной форме».

«Па второй полке 12 книг. Книг на второй полке в три раза больше, чем на первой. Сколько книг на первой полке?».

• • На какой полке количество книг известно? Сколько их?
• • Что известно о количестве книг на второй полке в сравнении с первой?
• • Что значит «в три раза больше»?
• • Если на второй полке книг в три раза больше, чем на первой, то на первой столько книг, количество которых, взяв три раза, получим количество книг на второй полке.
• • Рисуем схему (рис. 11.9), которая является переводом информации, заданной текстом, на язык знаков-индексов.

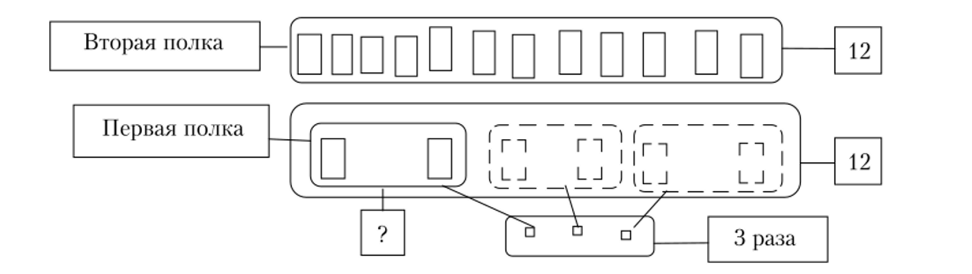
Рис. 11.9. Перевод текста на язык знаков-индексов

• • Значит, если число книг на первой полке умножить на 3, то получим 12. Это число есть частное 12/3.
• • Записываем решение: 12/3 = 4 (книги).

Ответ: 4 книги на первой полке.

Как правило, знакомство с простой задачей, решение которой состоит в выборе действия (сложения или вычитания) и записи соответствующего выражения, происходит в 1-м классе. Например, непосредственно вслед за изучением нумерации чисел первого десятка начинается формирование представлений о текстовой задаче в системе «Школа 2100». Вводятся термины: задача, условие, вопрос, схема, выражение, значение выражения, ответ.

Зачастую опорой в поиске решения выступают понятия целого и части, обозначаемые отрезками. Выделяются схемы: нахождение целого, нахождение части, определяющие выбор арифметического действия. Так, формирование умений решать простые задачи на сложение и вычитание с опорой на понятия целого и части реализуется в системе Б. Д. Эльконина — В. В. Давыдова. Первоначально моделируются ситуации, обозначаемые рассказами о значениях величин. Например, текст «В вазе было а груш. Из них b груш съели. Осталось с груш» моделируется следующей схемой¹.

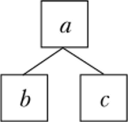
Выбор действия, когда требуется найти значение величины, представленной отношением «целое — часть», регламентируется правилами:

• • чтобы найти целое, нужно сложить части;
• • чтобы найти часть, нужно из целого вычесть известную часть^[2][3].

В то же время отношение между величинами в задаче «Оле нужно было решить 12 примеров. Через 5 мин остались нерешенными два примера. Сколько примеров Оля решила за 5 мин?»^[4] не обеспечивается прямолинейной апелляцией к понятиям целого и части, в ситуацию внесены дополнительные параметры, не влияющие на выбор действия, но затрудняющие се осознание.

Тот факт, что одни и тс же действия могут приводить к решению в совершенно различных ситуациях, делает особенно актуальной задачу обучения умению ориентироваться в различных по своей конкретной природе отношениях между величинами, наглядное истолкование которых на всех этапах рассуждения составляет одну из основных задач обучения математике.

Например, следующие внешне различные задачи, составленные И. В. Арнольдом еще в 1944 г., имеют одно и то же решение — 3 — 1.

• 1. Глубину водоема измеряли трехметровым шестом. Когда нащупали дно, длина оставшейся над уровнем воды шеста оказалась равной 1 м. Какова глубина водоема?
• 2. Час назад самолет должен был прибыть в аэропорт, но он опаздывает на 3 ч. Через сколько часов прибудет самолет?
• 3. Масса кирпича вместе с лопатой равна массе 3 кирпичей. Масса кирпича 1 кг. Какова масса лопаты?
• 4. За 3 ч лодка проплывает 3 км в стоячей воде, а бревно вниз по течению — 1 км. Сколько километров проплывет лодка за то же время вверх по течению?
• 5. От нашего дома до станции 3 км, а от почты до станции по той же дороге — 1 км. Каково расстояние от нашего дома до почты?

Эти задачи с некоторой натяжкой можно отнести к типу «нахождение остатка». Возможность нахождения решения каждой из приведенных задач опирается на конкретное видение ситуации, в которой доминирующими являются не числовые данные, а причинно-следственные связи между величинами. Вследствие чего возможность решения опирается не только на собственно математические знания, но и на житейский опыт, здравый смысл, развитое воображение, умение строить умозаключения. Такие качества мышления и формируются в первую очередь в деятельности по решению текстовых задач.

Простые текстовые задачи играют при этом значительную роль, если создаются условия для понимания текста как способа неявного задания искомого математического объекта, что предполагает формирование умений самостоятельно осуществлять перевод вербального текста как на язык знаков-икон, так и на язык знаков-индексов. Это значит, что необходимо учить ребенка самостоятельно создавать визуальные представления информации, заданной текстом, если они ему необходимы. Причем способы перекодирования информации, представленной текстом, могут изобретаться самим учеником в соответствии со своим «видением» данной конкретной ситуации. Главное, чтобы изобретенная схема — результат творческого поиска — могла помочь найти решение. Учителю важно поощрять подобного рода поиски, но никак не отвергать их, даже в том случае, если они не вполне корректны.

Это значит, что процесс обучения должен обеспечить максимально возможное разнообразие задач, включая нестандартные, тем более что наши младшие школьники, как показывают результаты международных мониторингов (по данным Н. Ф. Виноградовой), часто оказываются беспомощными в проблемных ситуациях, имеющих истоки в жизненных коллизиях, выяснение сути которых, вообще говоря, обеспечивается полученными в школе знаниями. Можно предположить, что умение решать типовые задачи не формирует умения применять знания в нестандартных ситуациях.

Простые задачи, решаемые действиями умножения и деления, вводят ученика в проблемную ситуацию, объекты которой связаны пропорциональной зависимостью, исключительно важной как в обыденной жизни, так и для дальнейшего изучения не только математики. Задачи «В шкафу.

3 полки, на каждой полке 8 книг. Сколько книг в шкафу?" и «Сколько литров сока в трех двухлитровых пакетах?» относятся к типу «нахождение суммы одинаковых слагаемых». Но суть их все же различна хотя бы потому, что в одной рассматриваются числовые значения дискретных величин, а в другой — непрерывных.

Смысл задачи про сок значительно ближе смыслу задачи «Со скоростью.

4 км/ч пешеход шел 2 ч. Какова длина пройденного им пути?", которая в рамках данной классификации есть также задача нахождения суммы одинаковых слагаемых. Так как в приведенных задачах и число пакетов, и время движения могут изменяться при сохранении значений вместимости и скорости, то задачи такого вида часто даются в нескольких вариантах: ответить на вопрос задачи, если число пакетов (время движения) 3, 4, 5.

Можно и нужно, обсуждая полученные результаты, помочь учащимся выразить эту зависимость в самом простом виде: чем больше пакетов, тем больше сока помещается в них; чем дольше шел пешеход, тем больший путь прошел. Апелляция к житейскому опыту и естественному смыслу рассматриваемых величин приближает рассматриваемую ситуацию к реальности, знакомой детям, что помогает увидеть за знаками суть дела. С другой стороны, если вместимость пакета естественно обозначить 2 л/пак., то и запись решения обеих задач совершенно аналогична:

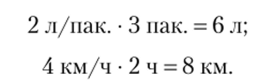
Запись решения с указанием единиц величины, т. е. размерности, могла бы уменьшить трудности, связанные с решением задач, указывая в самой записи отношение между конкретными величинами в реальной ситуации, а не абстрактную зависимость между числами. Тем более что, согласно мнению одного из выдающихся математиков современности В. И. Арнольда, «математика подобно физике экспериментальная наука. Выхолощенное и формализованное преподавание математики на всех уровнях сделалось, к несчастью, системой»^[5].

Если обратиться к определению умножения по Лобачевскому (см. подпараграф 3.1.2), то перевод на язык знаков-индексов количественных характеристик дискретных величин в задаче «Кате надо посадить три ряда розовых кустов по четыре куста в каждом ряду. Сколько розовых кустов ей потребуется?» представляется на рис. 11.10.

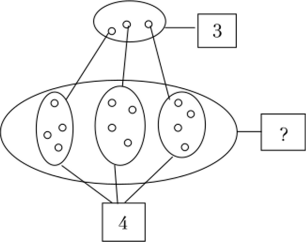
Рис. 11.10. Кодирование информации «По четыре куста в каждом из трех рядов» знаками-индексами.

Каждая единица, обозначающая количество рядов, замещается четырьмя единицами, обозначающими количество кустов в одном ряду. Следующие задачи фактически того же типа, но описание ситуации не так прямолинейно, что и делает их полезными с точки зрения формирования умений не ориентироваться на шаблон.

• 1. У Кати трое друзей. Сколько конфет надо взять Кате, чтобы каждому из них дать по две конфеты?
• 2. Мартышки в зоопарке размещены в трех клетках. В каждую клетку посадили еще по две обезьянки. На сколько больше обезьянок стало в этих клетках?

Задача «Сколько елочных шариков в коробке, если шарики в ней двух размеров: большие и маленькие, а шарики каждого размера трех цветов: красного, синего и желтого?» также является простой задачей на умножение.

Кодирование информации, представленной текстом, в форме таблицы (рис. 11.11) продиктовано определением произведения как мощности декартова произведения множеств, мощности которых — перемножаемые числа. Эта же информация может быть закодирована графом-деревом (рис. 11.12).

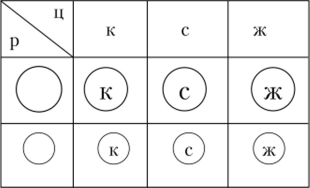
Рис. 11.11. Кодирование знаками-иконами декартова произведения.

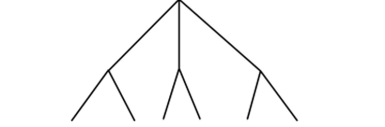
Рис. 11.12. Кодирование умножения графом-деревом Исходящие из «корня» «веточки» обозначают цвет шариков, а следующий ряд «веточек» — размер шариков. Такое представление умножения позволяет решать целый ряд комбинаторных задач. Например, «У Кати есть две блузки и три юбки. Сколько разных нарядов может надеть Катя из юбки и блузки?», или «На тарелке лежат четыре яблока и три груши. Сколькими различными способами Петя может взять одно яблоко и одну грушу?».

Для задач, речь в которых идет о числовых значениях непрерывных величин, следует обратиться к определению умножения на основе мультипликативности меры, согласно которому умножение есть переход к новой мере, представляющее собой произведение числового значения данной величины, выраженной в исходных единицах, на числовое значение исходной единицы, выраженной в новой единице (см. подпараграф 3.1.2). Примером задачи такого рода может служить следующая: «В бидоне помещаются три кружки молока. В каждой кружке две чашки. Сколько чашек молока в бидоне?» Перевод данной информации на язык знаков-индексов представлен на рис. 11.13.

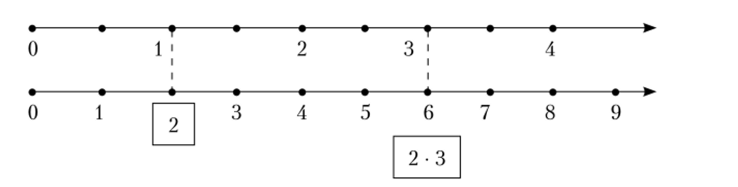
Рис. 11.13. Представление произведения чисел — мер величины В силу свойства мультипликативности меры, мера объема в кружках, равная 3, в новой единице — чашке, равна 2 • 3, так как объем одной кружки в чашках равен 2.

Задача «Шаг папы в два раза длиннее шага Пети. От песочницы до скамейки папа делает четыре шага. Сколько шагов сделает Петя на этом же пути?» открывает возможность раскрытия учащимся смысла прямой пропорциональной зависимости между величинами: количество Петиных шагов во столько же раз больше количества папиных, во сколько раз длина папиного шага больше длины Петиного. Эта зависимость знаками-индексами может быть представлена так, как показано на рис. 11.14.

Тип составной задачи в некоторых случаях определяется типом простых, ее составляющих. В тех случаях, когда это имеет значение, например

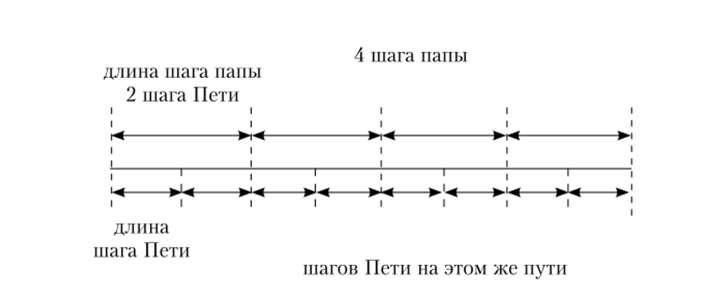
Рис. 11.14. Кодирование прямой пропорциональной зависимости при проверочных работах, в которые включаются задачи только в два действия, распознавание их типа обычно не вызывает затруднений. Имеются и специально выделенные типы составных задач. Например, задачи на нахождение неизвестного по двум разностям: «В детский сад привезли 24 кг моркови и 40 кг картофеля в ящиках одинаковой массы. Ящиков с картофелем привезли на 8 больше, чем ящиков с морковью. Сколько ящиков с картофелем и сколько с морковью привезли в детский сад?», или задачи на нахождение двух величин по их сумме и разности: «В двух бочках 60 л воды. В одной на 20 л больше, чем в другой. Сколько литров воды в каждой бочке?» Принято выделять тип задач «на части»: «В двух пакетах 16 кг картофеля. Сколько килограммов картофеля в каждом, если в одном картофеля в три раза больше, чем в другом?» Примером задачи на нахождение четвертого пропорционального является: «Туристы прошли 24 км за 6 ч. Оставшийся путь они прошли с той же скоростью за 3 ч. Сколько километров составил оставшийся путь?» Задача «В один день в ателье сшили 19 курток, в другой — 17 таких же курток. Всего было израсходовано 72 м ткани. Сколько метров ткани израсходовали в каждый из этих дней?» относится к типу «на пропорциональное деление».

В современных учебниках для начальной школы достаточно широко представлены нестандартные задачи. Среди них также выделяются определенные группы. Например, в следующих двух задачах искомое выражается через часть его самого.

• 1. Масса бочонка с медом 7 кг. Когда половину меда съели, масса бочонка с оставшимся медом стала 4 кг. Сколько килограммов меда было в бочонке?
• 2. Масса кирпича равна массе половины кирпича и еще 1 кг. Какова масса кирпича в килограммах?

Замечание, что масса, равная 7 кг — 4 кг, есть масса половины меда, сразу приводит к решению задачи 1. Вторая задача решается рассуждением: если масса половины кирпича и 1 килограмма равна массе кирпича, то масса половины кирпича также равна 1 кг, следовательно, масса кирпича равна 2 кг.

Задача «На дворе 10 цыплят и поросят, у них 26 ног. Сколько цыплят и сколько поросят на дворе?» имеет занимательный характер и относится к задачам, решение которых основывается на предположении о том, сколько было бы ног во дворе, если бы там гуляли только поросята (только цыплята). Действительно, предположив, что у всех животных по 2 ноги, получим 20 ног, значит, лишние 6 ног принадлежат поросятам, каждому по 2. К тому же типу относится задача из рассказа А. П. Чехова «Репетитор»: «Купец купил 138 аршин черного и синего сукна за 340 руб. Сколько аршин он купил того и другого сукна, если синее стоило 5 руб. за аршин, а черное — 3 руб.?».

В последнее время в начальную школу стали активно внедряться задачи комбинаторные, на взвешивание, на переливание. Так, задача «В шахматном турнире участвовало семь человек. Каждый с каждым сыграл по одной партии. Сколько партий они сыграли?» решается рассуждением: пусть шахматисты получили номера от 1 до 7, первый сыграл с остальными шестью, второй с пятью, так как его партия с первым уже учтена, и т. д., неучтенных партий, сыгранных последним, одна. Получаем сумму.

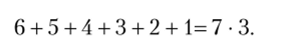
Решение задачи «Из 3 одинаковых колец одно легче остальных. Найти его одним взвешиванием на чашечных весах без гирь», состоящее в том, что сравниваются одним взвешиванием любые два кольца, обобщается на число колец, равное 3″, среди которых более легкое находится п взвешиваниями.

Логические задачи также уверенно входят в начальное образование. Например, поиск ответа в задаче «На заводе работают три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика» приводит к рассуждению: так как Семенов старше токаря, он не токарь и не слесарь, так как слесарь самый младший, следовательно, Семенов сварщик. У слесаря нет ни братьев, ни сестер, он не Борисов, у которого есть сестра, и не Семенов, значит, Иванов слесарь, а Борисов токарь.

Задачи, решение которых опирается на принцип Дирихле, встречаются во внеурочной работе по математике. Например, задача «В коробке лежат карандаши: семь красных и пять синих. В темноте берут карандаши из коробки. Сколько надо взять карандашей, чтобы среди них было не меньше двух красных и не меньше трех синих?» решается исследованием наихудшего варианта. Допустим, все выбираемые подряд карандаши оказываются синими, их семь, тогда достаточно взять еще два карандаша, чтобы удовлетворить требованию, т. е. надо взять девять карандашей.

Разумеется, приведенные примеры не исчерпывают всего многообразия нестандартных задач, но они в определенной мерс могут ориентировать будущего учителя, который должен уметь направлять мысль детей на поиск их решения.

Задания для самостоятельной работы

• 1. Приведите примеры простых задач первой группы по одной каждого типа. В случае затруднений обратитесь к учебнику методики авторов М. А. Вантовой и Г. В. Бельтюковой. Подготовьте сообщение.
• 2. Приведите примеры простых задач второй группы, но одной каждого тина. Подготовьте сообщение.
• 3. Приведите примеры простых задач третьей группы по одной каждого типа. Подготовьте сообщение.
• 4. Докажите, что зависимость между величинами в следующих задачах одна и та же и кодирование информации знаками-индексами в этих задачах совпадает.
• • В одной коробке три фломастера. Сколько фломастеров в пяти таких коробках?
• • Тюбик рисует каждый портрет малышки в Зеленом городе одно и то же время. За это время Незнайка успевает дать три указания. Сколько указаний дал Незнайка за время написания Тюбиком пяти портретов?
• • 11орция мороженого стоит три монеты. Сколько монет нужно Буратино, чтобы купить пять порций мороженого?

Нарисуйте схему на языке знаков-индексов. Подготовьте презентацию.

• 5. В задаче «Для посадки привезли 20 лип и 40 дубков. Их посадили в ряды поровну. При этом лип получилось на пять рядов меньше, чем дубков. Сколько рядов лип и рядов дубков получилось?» выделите простые задачи, составляющие данную. Сформулируйте каждую из них. Например, «Для посадки привезли 20 лип и 40 дубков. Насколько меньше привезли лип, чем дубков?». Определите тип каждой простой задачи. Подготовьте сообщение.
• 6. Составьте задачу, если на языке знаков-индексов зависимость между величинами представлена следующей схемой.

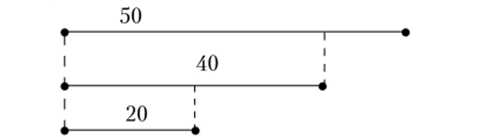
Переведите текст на язык знаков-икон. Подготовьте презентацию.

• 7. Составьте список различных нестандартных задач из учебника математики для 1—4-го классов системы «Школа 2100». Подготовьте сообщение.
• 8. Разработайте задания листа рабочей тетради, цель которых — раскрыть смысл отношения: а) «больше на несколько единиц»; б) «больше в несколько раз». Подготовьте презентацию.
• 9. Постройте перевод сообщения «Из одного и того же пункта в одном направлении выехали два автомобиля, один со скоростью 40 км/ч, другой со скоростью 60 км/ч» на язык знаков-индексов. Подготовьте сообщение.
• 10. Решите следующие задачи, нарисовав схему знаками-индексами.
• • На покупку тетрадей и альбомов есть 480 руб. Нужно купить 16 тетрадей по 7 руб. Сколько тетрадей можно купить на оставшиеся деньги, если цена альбома 8 руб.
• • От поселка до озера 12 км. С какой скоростью надо идти, чтобы дойти до него за 3 часа? Сколько времени понадобится, если уменьшить скорость в 2 раза?
• • Хватит ли машине 10 л бензина, чтобы доехать до заправочной станции, если расстояние до заправочной станции 120 км, а на каждые 100 км пути машина затрачивает 5 л бензина?
• • От, А до В автомобиль шел со скоростью 40 км/ч, а обратно — со скоростью 60 км/ч. Какова средняя скорость автомобиля за весь рейс?
• 11. Решите следующие нестандартные задачи^[6]:
  • • Четыре брата, Юра, Петя, Вова и Коля учатся в 1,2,3,4-х классах. Петя учится только на 4 и 5, а младшие братья стараются брать с него пример. Вова уже изучает историю России, а Юра помогает решать задачи брату. Кто из них в каком классе учится?
  • • Вдоль беговой дорожки равномерно расставлены столбы. Старт дан у первого столба. Через 12 минут бегун был у четвертого столба. Через сколько минут от начала движения бегун будет у седьмого столба, если его скорость постоянна?
  • • Незнайка может съесть 480 г варенья за б минут, а Пончик — в два раза быстрее. За сколько времени они съедят это варенье вместе?
  • • Путь от дома до школы Буратиио проделал пешком. Обратно он двигался той же дорогой, но первую половину пути проехал на собаке, а вторую — на черепахе. Скорость собаки в 4 раза больше скорости черепахи, а скорость черепахи в 2 раза меньше скорости Буратино, с которой он шел в школу. На какой путь — из дома до школы или из школы до дома — затратил Буратино больше времени?
• 12. Книга стоит 100 рублей и еще половину стоимости книги. Сколько стоит книга?

• [1] Баптова М. А., Бельтюкова Г. В. Методика преподавания математике в начальныхклассах. М.: Просвещение, 1984. С. 198—199.
• [2] Давыдов В. В., Горбов С. Ф., Микулина Г. Г. Математика. 1 класс. М.: Мирос, 1999.
• [3] Там же. С. 138, 142.
• [4] Давыдов В. В., Горбов С. Ф., Микулина Г. Г. Математика. 1 класс. М.: Мирос, 1999. С. 145.
• [5] Арнольд В. И. Математика и математическое образование в современном мире // Математическое образование. 1997. № 2. С. 109—112.
• [6] Задачи взяты из сборников, составленных В. Н. Русановым, В. Ю. Сафоновой.