Введение. 
Математическое моделирование

Моделирование — это замещение одного объекта (оригинала) другим (моделью) и фиксация или изучение свойств оригинала путем исследования свойств модели.

Трудно переоценить роль моделирования в научных исследованиях и инженерной работе. Разработка и познание любой системы сводится по существу, к созданию ее модели. Особую ценность имеют конструктивные модели, т. е. такие, которые допускают не только фиксацию свойств, но и исследование зависимостей характеристик от параметров системы.

Модель объекта — это физическая или абстрактная система, адекватно представляющая объект исследования. В теории моделирования используются преимущественно абстрактные модели — описания объекта исследования на некотором языке. Абстрактность модели проявляется в том, что компонентами модели являются не физические элементы, а понятия, в качестве которых наиболее широко используются математические. Абстрактная модель, представленная на языке математических отношений, называется математической моделью.

Математическая модель — это совокупность уравнений (алгебраических, дифференциальных, интегральных), описывающих процессы, происходящие в моделируемом явлении. Результатом математического моделирования являются формулы (если удается получить аналитическое решение уравнений модели), которые позволяют рассчитать характеристики моделируемого процесса или таблицы значений этих характеристик (если аналитическое решение получить не удается, либо оно не очень удобно). Чаще всего встречается именно последний случай, когда решение можно получить лишь в виде таблицы с помощью каких-либо вычислительных процедур. Такого рода модели носят специальное название численных моделей. Специфика этих моделей состоит в том, что они позволяют получить принципиально приближенное решение, что связано с дискретностью вычислительных устройств, ограниченным объемом памяти, конечным быстродействием и т. п. Наша цель — научиться исследовать алгоритмы получения численного решения уравнений модели.

Движение систем малого числа частиц математически описывают, как правило, обыкновенными дифференциальными уравнениями. Если же число частиц очень велико, то следить за движением отдельных частиц практически невозможно. При этом удобнее рассматривать систему частиц как сплошную среду, характеризуя ее состояние средними величинами: плотностью, температурой в данной точке и т. д.

Математические модели сплошной среды приводят к уравнениям в частных производных, которым удовлетворяют упомянутые средние величины. Например, изменение температуры в неподвижном теле описывается уравнением теплопроводности.

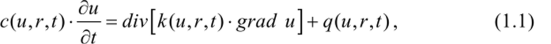
где и — температура; с — теплоемкость; к — коэффициент теплопроводности; q — плотность источников тепла.

К уравнениям в частных производных приводят задачи газодинамики, теплопроводности, переноса излучения, распространения нейтронов, электромагнитных полей, теории упругости, процессов переноса в газах, квантовой механики и многие другие.

Независимыми переменными в физических задачах обычно являются время t и координаты г; бывают и другие переменные, например, скорости частиц v в задачах переноса. Решение требуется найти в некоторой области изменения независимых переменных G (t, r, v,…). Полная математическая постановка задачи содержит дифференциальное уравнение, а также дополнительные условия, позволяющие выделить единственное решение среди семейства решений дифференциального уравнения. Дополнительные условия обычно задаются на границе области G.

Если одной из переменных является время t, то чаще всего рассматривают области вида.

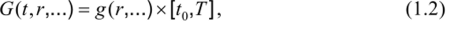
т. е. решение ищут в некоторой пространственной области g (r,…) на отрезке времени t₀ В этом случае дополнительные условия, заданные при t = t₀, называют начальными, а дополнительные условия, заданные на границе Г (г) области g®, — граничными или краевыми.

Задачу, у которой имеются только начальные условия, называют задачей Коши. Например, для уравнения теплопроводности (1.1) в неограниченном пространстве можно поставить задачу с начальными условиями Если ju® — кусочно-непрерывная ограниченная функция, то решение задачи (1.1), (1.3) единственно в классе ограниченных функций (при некоторых ограничениях на коэффициенты уравнения).

Задачу с начальными и граничными условиями называют смешанной краевой задачей или нестационарной краевой задачей. Для уравнения (1.1) дополнительные условия такой задачи могут иметь, например, вид.

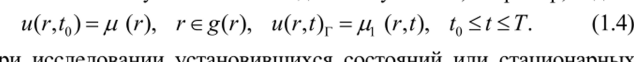
I Iptl MVWI^V'UUllIirj V V 1Ш IVUIlUllltmVA WVIVAlirm ПЛМ V, 1 ЫЦГ1,/11UI/1IUI/1.

(не зависящих от времени) процессов в сплошной среде формулируются математические задачи, не зависящие от времени. Их решение ищется в области g (r), а дополнительные условия являются граничными. Такие задачи называют краевыми.

В настоящем пособии мы ограничимся рассмотрением корректно поставленных задач, когда для некоторого класса начальных и граничных данных решение (в заданном классе функций) существует, единственно и непрерывно зависит от этих данных. Будем также предполагать, что решение непрерывно зависит от всех коэффициентов уравнения.

Многие задачи, о которых мы говорили, можно записать в операторной форме. Так, уравнение теплопроводности д, Т — рАТ + Q, волновое уравнение 8_UU = adJJ, или уравнение переноса некоторой величины С со скоростью v вдоль оси х д, С + vd_ХС = 0 можно записать в такой операторной форме: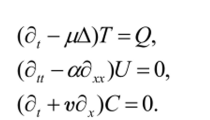

То, что записано в скобках, называется оператором. Если обозначить его через А, то все эти уравнения примут вид:

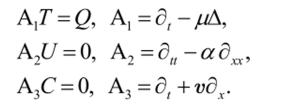
Операторное уравнение Af = g можно интерпретировать следующим образом. Пусть даны два множества функций F и G и пусть / есть элемент множества F, a g- элемент множества G. Оператор, А в этом случае указывает соответствие между элементами множеств F и G. И наша задача, зная g из G и вид оператора А, найти/из множества F.

Свойства линейных операторов и другие необходимые понятия функционального анализа приведены в приложении (п. 4).