Метрика и норма

Иначе говоря, значение суммы функций в точке х равно сумме значений функций-слагаемых в той же точке. Аналогично для а/. Аксиомы векторного пространства, очевидно, выполняются. Как правило, столь общие линейные пространства функций нс рассматривают, а изучают подмножества F, которые, в свою очередь, также образуют линейные пространства, например, пространство С°() непрерывных функций… Читать ещё >
Метрика и норма (реферат, курсовая, диплом, контрольная)
Выше мы уже использовали понятие расстояния, не оговаривая, как его измерить. Рассмотрим этот вопрос подробнее. Если бы мы ограничивались точками на прямой, плоскости или в трехмерном пространстве, то интуитивно все было бы понятно. Однако теперь точками мы называем элементы векторных пространств. Что же вкладывается в понятие расстояния между ними? Поскольку плоскость — это частный случай векторного пространства, то и под расстоянием между точками векторного пространства мы будем понимать нечто аналогичное расстоянию между точками на плоскости. Во-первых, расстояние есть неотрицательное число. Во-вторых, оно зависит от взаимного расположения точек и не зависит от их положения относительно нуля. В-третьих, неважно, как мы измеряем расстояние: от первой точки ко второй или наоборот. В-чствсртых, если точки совпадают, то расстояние между ними равно нулю. И, наконец, если мы рассматриваем расстояния между тремя точками, то любое из них не превышает суммы двух других (длина стороны треугольника не превышает суммы длин двух других сторон). Вот такими же свойствами мы наделим и расстояние между точками любого векторного пространства или даже просто произвольного множества (ведь на плоскости расстояние между двумя точками имеет смысл и тогда, когда мы рассматриваем лишь какую-то ее часть, а не всю целиком). Формально все, что было сказано, запишется так. Пусть X — произвольное множество и f, g, heX. Поставим каждой паре /и g в соответствие неотрицательное число d (J', g), такое, что для любых f, g и к из X справедливо:
- 1) d (f, g)>0, если / * g;
- 2) d (f, f)= 0;
- 3) d (f, g) = d (g, f);
- 4) d (f, g)
Очевидно, что d (f, g) есть функция (отображение), определенная на любой паре векторов из X со значениями в числах (в /?'). Определенная так функция называется метрикой на X, а само X, снабженное метрикой (или, как говорят, пара {X, d)), — метрическим пространством. Обратите внимание, что для того, чтобы некоторое множество стало метрическим пространством, на нем необходимо ввести метрику и только. При этом оно, естественно, не становится векторным пространством, ибо на нем еще не определены сложение элементов и умножение их на число. В том случае, когда мы работаем с векторным пространством V, можно воспользоваться тем, что у нас уже есть одна выделенная точка 0, и ввести более сильное понятие нормы вектора, т. е., по сути, расстояние от элемента до 0. Поскольку здесь предполагается наличие некоторого правила, ставящего в соответствие каждой точке из V вещественное число, которое мы называем расстоянием до точки 0, мы имеем функцию (отображение), отображающую V в R1. Для обозначения нормы используется специальный значок II • II. Норма вектора/обозначается ||/||. Запишем определение нормы формально для более общего комплексного случая, который нам понадобится впоследствии. Пусть V- векторное пространство и /е V. Нормой вектора / называется неотрицательная числовая функция ||/||, определенная на V, такая, что для любых f и /у <= R1 ВЫПОЛНЯЮТСЯ условия:
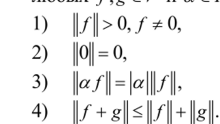
(неравенство треугольника).
Заменой элемента g на (А — /) и последующим переобозначением легко получить и другие варианты неравенства треугольника. Все их можно записать в виде следующих неравенств:
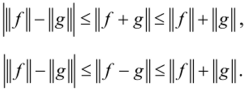
Линейное пространство, снабженное нормой, называется нормированным векторным пространством. Если для каждой точки V известно ее расстояние до нуля (норма), то легко условиться и о том, как измерить расстояния между точками из V, т. е. получить метрику. Для этого расстоянием между двумя точками/и g можно считать норму их разности.

Данное выше определение нормы не задает нам ее единственным образом. Часто для одного и того же векторного пространства можно ввести несколько норм. Получающиеся при этом нормированные пространства считаются разными.
- 1. Линейное пространство R' становится нормированным, если нормой х элемента х е R' считать его модуль |х|. Очевидно, что такое определение нормы в /?' корректно.
- 2. В пространстве R" норму вектора х = (хх2можно ввести многими способами. Наиболее часто используются следующие нормы:
- а) октаэдрическая норма, или норма ||? || :


3. Наглядное представление об этих нормах дает множество элементов х е R" , для которых ||х|| = 1, или так называемая единичная сфера. В плоском случае, т. е. для R2, единичная сфера для разных норм показана на рис. 30.
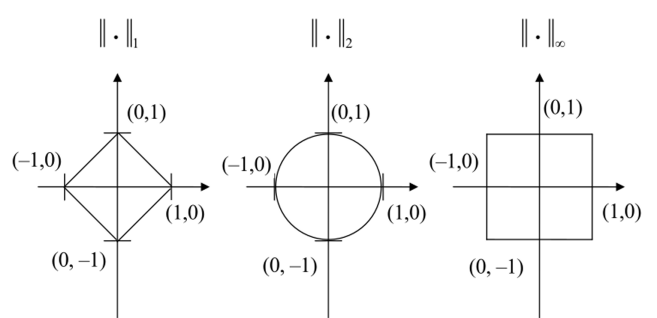
Рис. 30. Вид единичной сферы на R2 для разных норм.
4. Весьма важными являются векторные пространства, элементы которых есть функции (т. е. функции будут в этом случае точками или векторами данного пространства). Рассмотрим множество /г([а,/>]) вещественных функций, определенных на отрезке [а, Л]. Пусть.
J', geF и a € R]. Определим новые функции f + g и а/, считая, что ДЛЯ ВССХХ€[й, Ь] 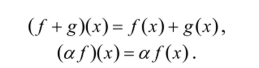
Иначе говоря, значение суммы функций в точке х равно сумме значений функций-слагаемых в той же точке. Аналогично для а/. Аксиомы векторного пространства, очевидно, выполняются. Как правило, столь общие линейные пространства функций нс рассматривают, а изучают подмножества F, которые, в свою очередь, также образуют линейные пространства, например, пространство С°([я,/>]) непрерывных функций, определенных на [а, Ь, или пространство С* ([",?]) функций, обладающих к ограниченными непрерывными производными на [я, Л]. Функциональные линейные пространства, как правило, бесконечномерны. Эти пространства также можно сделать нормированными, если построить для них соответствующую норму. Так, С°([а,/?]) часто снабжается так называемой равномерной нормой

Очевидно, что это бесконечномерный аналог нормы || •. Другая возможная норма — норма || • .:

Существуют и иные варианты норм. Равномерной норме можно дать наглядную интерпретацию. Пусть М — множество функций, таких, что |/"1 < а, для всех /(х) е М и а > 0, а е R'. Тогда все/из М должны «укладываться» в полосу ±а относительно оси абсцисс (рис. 31).
Если Р — множество функций /, для которых расстояние от заданной функции g не превышает у?, т. е. ||/ -g||< /3, то все изменения/ должны быть заключены в полосе шириной 2Д, охватывающей функцию g. Для нормы I • I, это не так, поскольку ограничиваться будет лишь интеграл, а значения функции в отдельных точках могут этому ограничению не удовлетворять. Ограничение ||/(х)|| < а, таким образом, более сильное, нежели ||/|| < а, и из первого следует второе, но не наоборот.