Примеры разностных схем. 
Явные и неявные разностные схемы

Пример 1. Разностная схема для уравнения Пуассона, относящегося к эллиптическому типу.

Рассмотрим построение разностной схемы для первой краевой задачи для уравнения А и = f (x, y) в области, представляющей собой прямоугольник со сторонами, параллельными осям координат. Пусть с этим прямоугольником связана равномерная сетка с шагами h_x и h_y .

Краевую задачу.

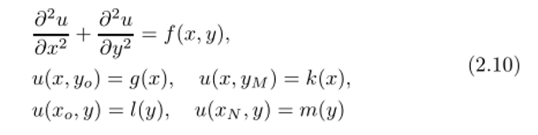
можно записать в операторной форме:

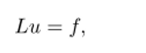
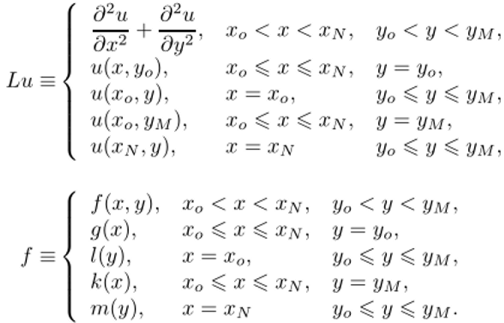
Отметим, что в эту запись включены и граничные условия.

Заменив дифференциальные операторы разностными, получим уравнения.

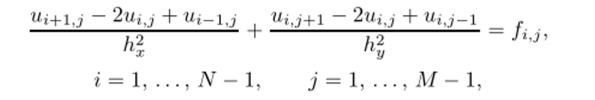
которые аппроксимируют исходное дифференциальное уравнение со вторым порядком 0(h² + h²) точности и действуют во всех внутренних точках области.

Разностные аналоги краевых условий будут иметь вид.

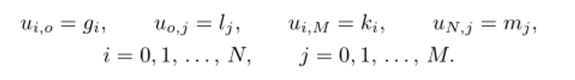
Разностная аппроксимация дифференциального уравнения совместно с разностными аналогами краевых условий образуют разностную схему для уравнения Пуассона.

Разностную схему можно по аналогии с краевой задачей записать в операторном виде:

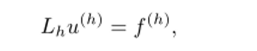
где в L/, включены как разностное уравнение, так и разностное краевое условие:

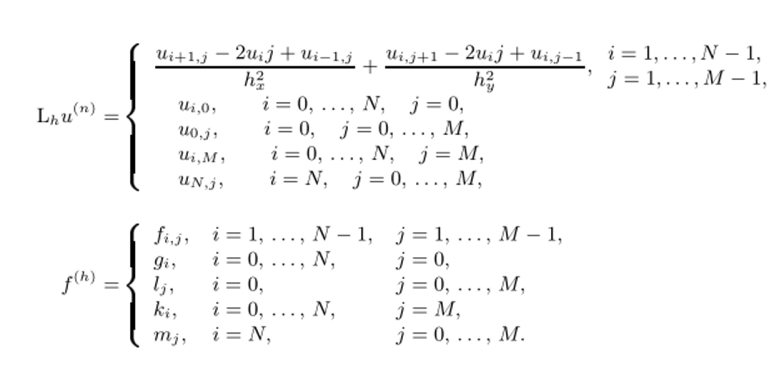
Разностное уравнение связывает значения сеточной функции в пяти точках, образующих разностный шаблон для этого уравнения. Для данного случая этот шаблон называют крест. Можно представить и другие шаблоны для этого уравнения.

Мы получим приближенное решение дифференциальной краевой задачи, если определим значения сеточной функции во всех внутренних узлах области. Для этого необходимо решить совместно систему алгебраических линейных уравнений, размерность которой равна количеству внутренних узлов области. В этом случае говорят о неявной разностной схеме. Любое интересующее нас значение Uij можно определить лишь из решения всей разностной задачи.

Относительно системы уравнений отметим два обстоятельства.

• 1. Система имеет очень высокую размерность (М — 1) х (N — 1), а традиционные методы точного решения (например, метод Гаусса) требуют для решения число алгебраических операций, пропорциональное третьей степени размерности системы.
• 2. В матрице системы много нулевых элементов (неплотная матрица). Это обстоятельства позволяет разработать экономичные методы приближенного решения.

Рассмотренная постановка разностной задачи характерна для эллиптических уравнений. В газовой динамике такой вид имеет уравнение для функции тока или для потенциала скорости. В других разделах мы рассмотрим эффективные методы разрешения таких разностных схем.

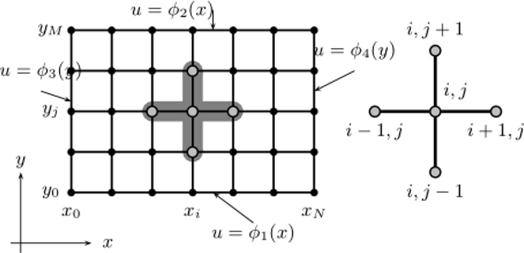
Рис. 2.8. Сетка и разностный шаблон для уравнения Пуассона.

П р и м с р 2. Разностная схема для простейшего параболического уравнения (нестационарная теплопроводность в стержне единичной длины).

Рассмотрим следующую задачу:

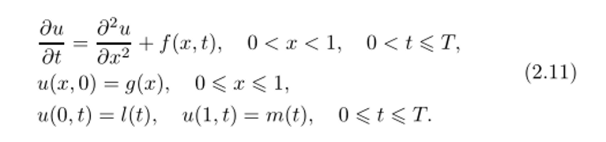
Отмстим, что в случае параболического уравнения имеем открытую область. При построении разностной схемы возникают несколько вариантов связи между разностными производными по пространству и по времени.

Проинтегрируем уравнение в пределах одного временного шага:

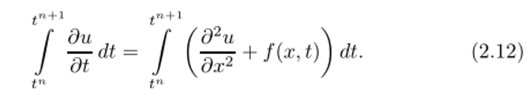
В зависимости от того, какую квадратурную формулу мы примем для вычисления интеграла в правой части, получим разные разностные схемы (рис. 2.9).

Связывая разностную производную по времени с пространственной производной, определенной на п-м временном слое, получим.

явную 'разностную схему

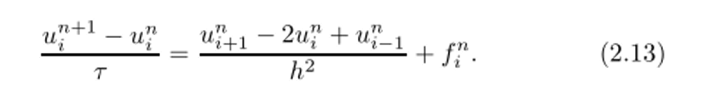
Это эквивалентно приближенному вычислению интеграла, стоящего в правой части (2.12), но способу левых прямоугольников.

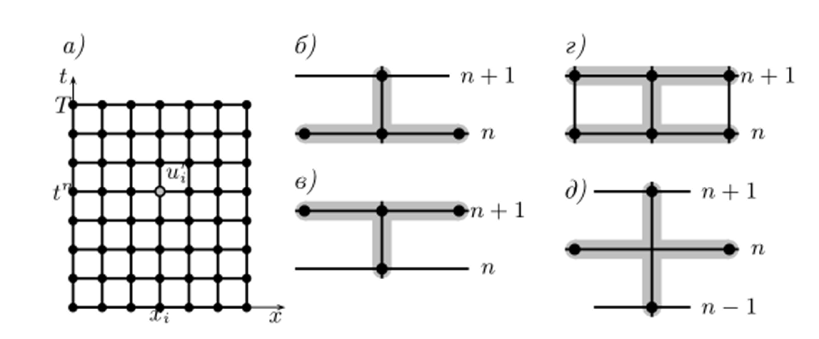
Рис. 2.9. Сетка и шаблоны для уравнения теплопроводности: а — область и сетка; б — шаблон явной схемы; в — шаблон неявной схемы; г — шаблон семейства шеститочечных схем; д — шаблон схемы.

«чехарда».

В приведенной формуле заключен и метод решения сеточных уравнений:

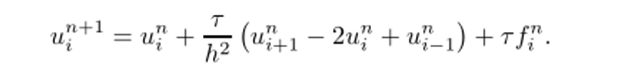
Значение сеточной функции на следующем временном слое определяется через известные значения гф на предыдущем. Перемещаясь последовательно слоями от начального условия и (х, 0) = у (х), можно найти решение во всей расчетной области. Разностный шаблон для этой схемы приведен на рис. 2.9, б.

Оценивая интеграл через значение подынтегральной функции па слое п + 1, используем разностный шаблон вида рис. 2.9, б, а разностный аналог дифференциального уравнения примет вид.

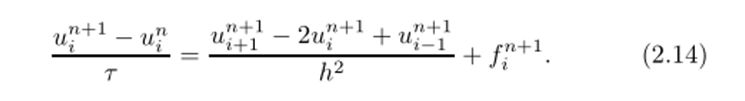
Для того чтобы найти значения сеточной функции на следующем временном слое, при использовании этой разностной схемы необходимо решить совместно столько уравнений вида (2.14), сколько внутренних узлов расположено на п —1−1 -м временном слое. С учетом краевых условий = /^п+1, Мд_Г⁺¹ = mⁿ⁺¹ система позволяет построить решение на следующем временном слое при известных значениях сеточной функции на предыдущем. Передвигаясь от начальных значений слоями, на каждом из которых необходимо решать систему уравнений, можно построить приближенное решение во всей области.

Рассмотренная разностная схема представляет собой пример неявной разностной схемы, ее называют схемой с опережением или чисто неявной схемой.

Шеститочечный разностный шаблон порождает семейство разностных схем, частными случаями которого являются две предыдущие:

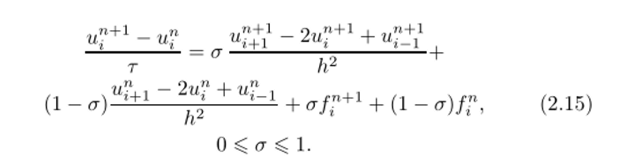
При а = 0 имеем явную схему, при а = I — неявную с опережением, при а > 0 — неявную. При а — 0,5 получаем широко известную в вычислительной практике симметричную схему Кранка Николсона.

Приведенные схемы, разумеется, не исчерпывают всего многообразия разностных схем, основанных на разностной аппроксимации дифференциальных операторов. Вот пример явной разностной схемы, основанной на центрировании временной производной, схемы, использующей сеточную функцию на трех временных слоях:

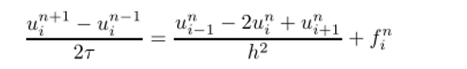
Разностный шаблон захватывает три временных слоя. Схема имеет второй порядок аппроксимации как по времени, так и по пространственной переменной и является явной. Эта схема обладает рядом существенных недостатков, от большей части которых можно избавиться, заменив и" в аппроксимации пространственной производной средним значением по двум временным слоям:

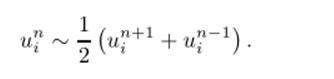
Полученная таким образом явная трехслойная схема.

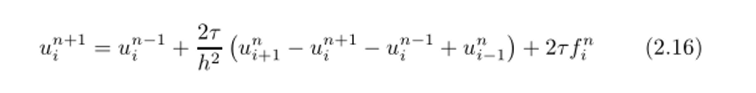
называется схемой Дюфортпа — Франкела, а отсутствие в ней значения сеточной функции в центральном узле объясняет название «чехарда», которое иногда применяется для схем такого рода.

На примерах было показано, что для одной и той же краевой задачи можно записать несколько разных разностных схем, т. е. в распоряжении исследователя имеется достаточно большой их выбор. Каким же условиям должна удовлетворять разностная схема, чтобы разностное решение соответствовало решению исходной дифференциальной задачи? Этот вопрос будет рассмотрен в следующем разделе.