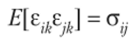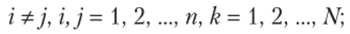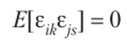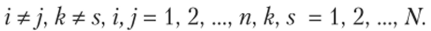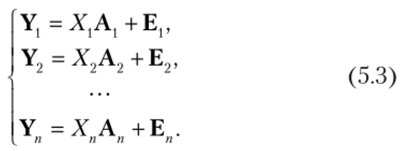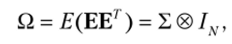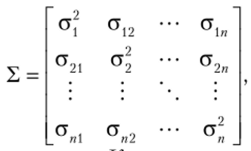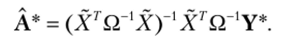Системы внешне несвязанных уравнений

Система внешне несвязанных уравнений [19] представляет собой систему независимых уравнений, в которой нарушено условие о независимости случайных ошибок разных уравнений друг от друга. Например, возможна корреляция между ошибками разных уравнений в одних и тех же наблюдениях, т. е.

при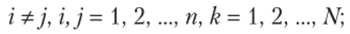

при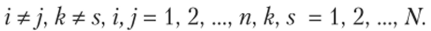

В связи с этим оценивание параметров каждого уравнения в отдельности невозможно, необходим совместный анализ таких уравнений. Для этого введем следующие обозначения:

где Y; — вектор значений /-й эндогенной переменной в N наблюдениях; — матрица значений экзогенных переменных, включенных в i-e уравнение системы; А_г — вектор неизвестных параметров /-го уравнения; Е_; — вектор случайных ошибок /-го уравнения в N наблюдениях.

С учетом этих обозначений запишем систему (5.2) в матричном виде:

Для совместного анализа объединим все уравнения системы (5.3) в одну модель множественной регрессии

где.

Ковариационная матрица вектора ошибок модели (5.4) имеет вид.

где 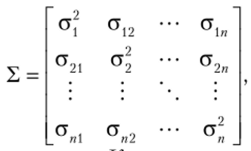а символом «®» обозначено произведение Кронекера двух матриц^[1] [19, 42].

Оценивание вектора неизвестных параметров модели (5.4) может быть проведено с использованием обобщенного метода наименьших квадратов (см. параграф 4.17):

При этом, естественно, предполагается, что матрица X невырождена. Как отмечено в работе [19], данные оценки будут совпадать с оценками, полученными для случая системы независимых уравнений, только в том случае, если для каждого уравнения системы (5.3) матрицы экзогенных переменных совпадают, т. е. Х_х = Х₂ = … = Х_п.

• [1] Произведением Кронекера, А 0 В матриц, А и В размерности тхпи рх q соответственно называется блочная матрица размерности тр х пцвида