Численные методы решения обыкновенных дифференциальных уравнений

В главе рассматриваются различные методы решения задачи Коши и краевой задачи для обыкновенных дифференциальных уравнений. Подробно рассмотрены метод Эйлера и ошибки, возникающие при его реализации на компьютерах; семейство одношаговых методов Рунге — Кутты, многошаговые методы. В качестве примеров методов решения краевой задачи излагаются методы стрельбы и разностный.

Основы теории обыкновенных дифференциальных уравнений

ОБЫКНОВЕННЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ называется уравнение вида.

связывающее одну независимую переменную х, искомую функцию у (х) и ее производные вплоть до п-го порядка. ПОРЯДКОМ обыкновенного дифференциального уравнения называется порядок старшей производной от искомой функции.

Дифференциальное уравнение называется ЛИНЕЙНЫМ, если оно имеет вид.

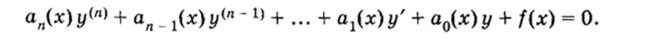
Так, например, у"  — х²у + х² = 0 — линейное дифференциальное уравнение второго порядка; у" + е^у — 0 — нелинейное уравнение.

ОБЩИМ ИНТЕГРАЛОМ уравнения (3.1) называют функцию.

связывающую независимую переменную х, искомую функцию у (х) и п постоянных интегрирования c_v … с" с помощью уравнения Ф (х, у, с…с_п) = 0. Таким образом, функция у (х) входит в функцию (3.2) неявным образом, причем число постоянных интегрирования равно порядку уравнения.

ОБЩИМ РЕШЕНИЕМ обыкновенного дифференциального уравнения называется функция.

связывающая независимую переменную и п постоянных интегрирования, иначе говоря, уравнение (3.3) определяет функцию у (х) явным образом.

Для определения постоянных интегрирования задаются ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ. Их число равно числу постоянных интегрирования. Если в дополнительные условия подставить функцию (3.2) и решить полученную систему относительно постоянных интегрирования c_t, …, с", а затем полученные решения подставить в (3.2), то получим ЧАСТНЫЙ ИНТЕГРАЛ Ф^х, t/(x)) — 0.

Аналогичные процедуры с общим решением (3.3) дают частное решение у{х) = (p_t(x).

Если все дополнительные условия задаются более чем в одной точке х₀, то совокупность обыкновенного дифференциального уравнения и дополнительных условий называют ЗАДАЧЕЙ КОШИ для рассматриваемого дифференциального уравнения. В этом случае дополнительные условия называют НАЧАЛЬНЫМИ УСЛОВИЯМИ.

Если дополнительные условия задаются более чем в одной граничной точке расчетной области, то совокупность обыкновенного дифференциального уравнения и дополнительных условий называют КРАЕВОЙ ЗАДАЧЕЙ для рассматриваемого уравнения, а дополнительные условия — ГРАНИЧНЫМИ или КРАЕВЫМИ УСЛОВИЯМИ.

КУТТА МАРТИН ВИЛЬГЕЛЬМ (Kutta Martin Wilhelm; 1867—1944) — немецкий физик и математик. В математике К. развил метод Рунге (метод Рунге — Кутты) численного решения задачи Коши для системы обыкновенных дифференциальных уравнений.

Таким образом, если задать числа у₀, y_v …" у_п_ _v то задача Коши для уравнения (3.1) имеет вид.

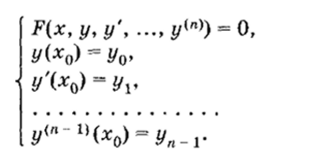
Порядок старшей производной в начальных условиях не превышает (п — 1), где п — порядок дифференциального уравнения.

Если старшая производная в уравнении выражается как функция переменных х, у и производных более низкого порядка, то уравнение называют РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО СТАРШЕЙ ПРОИЗВОДНОЙ и оно записывается в виде yW — = /(*, у, у', … у^{[п ъ}).

Задачу Коши для обыкновенного дифференциального уравнения л-го порядка у^{п) *= f (x, у, у yⁱⁿ~ ^J)) можно свести к задаче Коши для следующей нормальной системы уравнений.

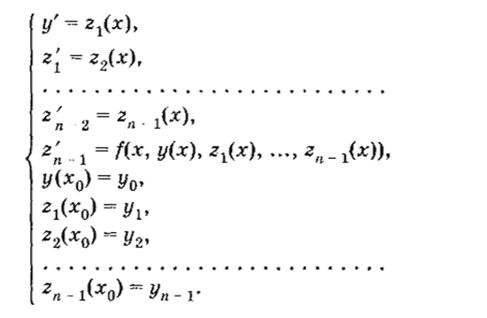
КОШИ ОГЮСТЕН ЛУИ (Cauchy Augustin Louis; 1789— 1857) — французский математик. В его курсах анализа, основанных на систематическом применении понятия предела, сформулировано представление о непрерывности функции, дано четкое построение теории сходящихся рядов (критерий Коши). В теории аналитической функции комплексного переменного К. дал выражение аналитической функции в виде интеграла Коши, получил разложение функции в степенной ряд. В теории дифференциальных уравнений К. поставил одну из важнейших общих задач, развил метод интегрирования уравнений с частными производными первого порядка. К. является одним из создателей теории упругости.

Здесь 2j (x), … z_k_, вводятся следующим образом:

ное уравнение.

Актуальность задачи Коши для многих областей науки и техники явилась причиной разработки для ее решения большого количества методов. Рассматриваются две группы численных методов решения задачи Коши.

• • ОДНОШАГОВЫЕ МЕТОДЫ, в которых для нахождения решения в некоторой точке отрезка используется информация лишь в одной предыдущей точке. К этим методам относятся методы Эйлера и Рунге — Кутты.
• • МНОГОШАГОВЫЕ МЕТОДЫ, в которых для отыскания решения в некоторой точке используется информация о решении в нескольких предыдущих точках. К таким методам относится метод Адамса.

Рассмотрим применение этих методов к дифференциальным уравнениям первого порядка. Алгоритм для случая системы дифференциальных уравнений легко получается из алгоритма для решения одного уравнения.

Необходимо отметить, что подобные методы можно применять только к хорошо обусловленным задачам, т. е. к таким задачам, решение которых мало изменяется в случае малого изменения начальных условий. В противном случае небольшие ошибки, которые неизбежны при решении задачи, могут существенно изменить решение.

ПРИМЕР. В качестве плохо обусловленной задачи рассмотрим решение следующей задачи Коши на отрезке [0, 100]:

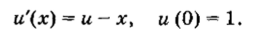
Общим решением этого дифференциального уравнения является.

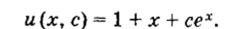
Из начального условия находим, что постоянная с — 0, поэтому и (100)=101.

Предположим, что начальное условие изменилось и и (0) ~ = 1,1. Следовательно, изменится и постоянная с в общем решении. В этом случае с = 10 ⁶ и решение имеет вид и (100) =.

= 2,7 • 10³⁷, т. е. изменение начального условия на 10'⁶ изменило решение на 35 порядков.

Постановка краевых задач для обыкновенных дифференциальных уравнений Постановку краевых задач для обыкновенных дифференциальных уравнений рассмотрим на примере уравнения второго порядка с переменными коэффициентами;

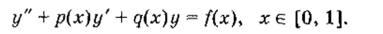
• Если на границах х = 0 и х ~ 1 заданы значения искомой функции, то такие граничные условия называются ГРАНИЧНЫМИ УСЛОВИЯМИ ПЕРВОГО РОДА, а задачу.

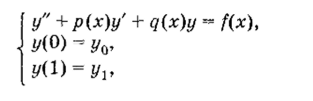
^гД^е Уо> .Vi — заданные числа, называют ПЕРВОЙ КРАЕВОЙ ЗАДАЧЕЙ.

• Если на границах х ~ О и х = 1 заданы значения производных искомой функции, то такие граничные условия называются ГРАНИЧНЫМИ УСЛОВИЯМИ ВТОРОГО РОДА:

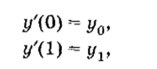
а соответствующая задача называется ВТОРОЙ КРАЕВОЙ ЗАДАЧЕЙ:

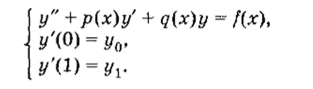
• Если на границах задана линейная комбинация первой производной и самой искомой функции, то такие граничные условия называются ГРАНИЧНЫМИ УСЛОВИЯМИ ТРЕТЬЕГО РОДА:

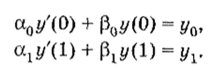
Такая задача называется ТРЕТЬЕЙ КРАЕВОЙ ЗАДАЧЕЙ: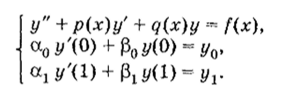

Очевидно, что если порядок обыкновенного дифференциального уравнения равен п, то порядок старшей производной в краевых условиях не может превышать значения (п — 1).

В заключение приведем одну из постановок краевой задачи для обыкновенного дифференциального уравнения четвертого порядка, встречающегося в теории упругости:

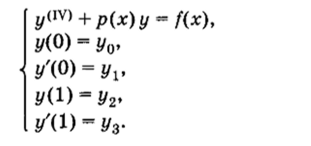
Здесь у₀, y_v у₂, у₃ — заданные числа.