Абсолютная величина М равна rFsin (a)

Второй закон Ньютона при вращательном движении. Момент инерции Угловое ускорение Р прямо пропорционально моменту силы М, приложенному к телу:

Уравнение вращательного движения в скалярной форме выглядит так:

Видна аналогия со вторым законом Ньютона для прямолинейного движения: а =(1 /то) F. Коэффициент пропорциональности (1//) определяет, насколько легко сообщить телу ускорение.

(здесь — угловое ускорение). Величина I — мера инерции тела по отношению к вращательному движению. Она называется моментом инерции тела. Чем больше I, тем труднее раскрутить тело.

Для второго закона Ньютона важны не отдельные силы, а их равнодействующая. В (2.78) при наличии нескольких сил на место М следует поставить равнодействующую всех моментов сил: М = М, + М₂ + … Может случиться, что сумма всех моментов сил равна нулю, т. е. моменты сил, вращающих тело в одну сторону, уравновешиваются моментами сил, вращающих в другую сторону. В этом случае тело будет покоиться или сохранять состояние равномерного вращения с постоянной угловой скоростью со.

Момент инерции I зависит не только от массы тела, хотя, конечно, чем массивнее тело, тем труднее сообщить ему угловое ускорение. Момент инерции определяется еще и распределением массы относительно оси. Чем дальше массивные части тела отстоят от оси, тем труднее раскрутить тело, тем больше момент инерции.

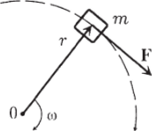
Рис. 2.41.

Возьмем тело небольших размеров на расстоянии г от оси вращения (рис. 2.41). Придать ему угловое ускорение значит одновременно сообщить и линейное ускорение а = dv/dt, где v — линейная скорость. Будем увеличивать v (и одновременно to), прикладывая силу F, перпендикулярную к г (рис. 2.41). Тогда по второму закону Ньютона для прямолинейного движения а = F/m, в то же время v = cor. В результате F/m = d (cor)/dt. Если тело находится на постоянном расстоянии г от оси, то F = mr (dw/dt) = mrp. Умножим обе части на г. Тогда слева получится момент силы М = Fr (угол между Биту нас равен 90° и sin (a) = 1):

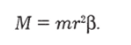
Сопоставив это с (2.79), видим, что для точечного тела.

Таким образом, момент инерции сильно (квадратично!) зависит от расстояния между точечным телом и осью вращения.

Тело произвольной формы следует разбить на малые части массой Ат и считать полный момент инерции I как сумму:

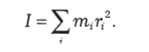
В пределе.

Интегрирование должно быть проведено по всему объему V тела.

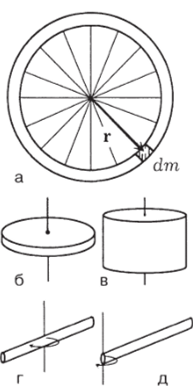
Для простых правильных форм это интегрирование производится сравнительно легко. Так, для колеса, масса которого распределена в основном по ободу (рис. 2.42, а), момент инерции относительно оси, проходящей через его центр перпендикулярно плоскости колеса, получается.

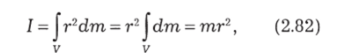aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">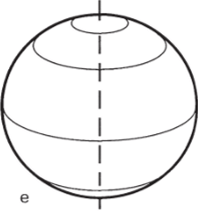

где т — масса всего колеса. Если же масса колеса распределена равномерно по диску (рис. 2.42, б), для момента инерции можно путем интегрирования получить

Такой же результат получается для однородного цилиндра относительно его собственной оси (рис. 2.42, в).

Для стержня длиной I, площадью поперечного сечения S и плотностью р (рис. 2.42, г) момент инерции относительно оси, проходящей, как показано р_ис 2.42.

на рисунке:

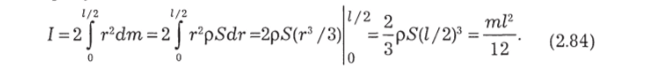
Для того же стержня, если он вращается вокруг оси, проходящей перпендикулярно к нему, но не через центр (рис. 2.42, д), момент инерции будет больше.

Приведем без вывода формулу момента инерции для однородного шара относительно оси, проходящей через центр (рис. 2.42, е):

Для тел неправильной формы моменты инерции рассчитываются численными методами.

Таким образом, задача об ускорении вращения тела под действием момента силы М решается в два этапа: сначала определяется момент инерции I по общей формуле (2.81) или по одной из формул (2.82)-(2.85), затем находится Р по формуле (2.78). Если угловое ускорение постоянно (что будет, если сумма всех вращающих моментов постоянна), то вращение называют равноускоренным. В этом случае формулы для конечной скорости со, для полного угла поворота аналогичны формулам (2.19)—(2.21), но с заменой S на <�р, v на со и а на Р:

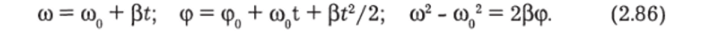
Обычно, как и при прямолинейном движении, такое случается очень редко. Например, момент сил трения сильно зависит от скорости. В результате вращение получается не равноускоренным (р * const). В этом случае использовать формулы (2.86) нельзя. Задачу надо решать на компьютере по программе, ядром которой будут строки постепенного наращивания со и ф:

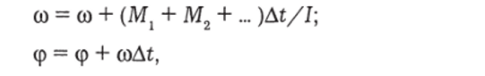
полученные из формулы (2.79).

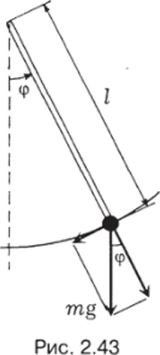
Пример. Рассмотрим маятник, т. е. груз на жестком подвесе длиной I (рис. 2.43). Выясним, зависит ли период колебаний маятника от амплитуды колебаний, т. е. от величины максимального угла отклонения.

Из рисунка следует, что вращающий момент не постоянен и зависит от угла отклонения: М = ragsin^). Момент инерции равен ml². Так что уравнение движения будет: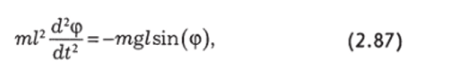

где ф (или зт (ф)) и угловое ускорение d²(p/dt² направлены в разные стороны. Поэтому поставлен знак «минус». При малых значениях углов Бт (ф) ~ ф (рад) и решение дифференциального уравнения (2.87) может быть найдено так: ф =^₀sin (cot). При подстановке этого решения в уравнение (2.87) получим период колебаний Т = 2п/со = 2к yjl/g. Однако при больших амплитудах замена Б1п (ф) на ф недопустима. В этом случае дифференциальное уравнение (2.87) аналитически решается очень сложно. С помощью же компьютера его можно решить хотя и приближенно, однако весьма просто. Точность решения зависит от величины шага At, т. е. от времени вычислений, и может быть достигнута сколь угодно большой.

Уравнения для постепенного наращивания со, ф и t будут иметь вид:

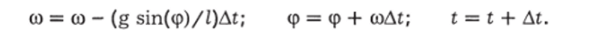
Таким образом, задав начальные условия: t = О, (О = 0, (р = <�р₀ (максимальное отклонение, амплитуда), мы можем постепенным наращиванием найти значения со и ср в любой момент времени. Остановим наращивание, когда ср будет равно нулю, и выведем время. Оно будет соответствовать четверти периода.

Введем обозначения переменных: / = L; ф = у; ф₀ = у 1; со = w; At = dt. Тогда программа на Бейсике будет:

Print «Зависимость периода кол. маятн. от амплитуды» PI=3.14: L=0.5: g=9.81

Input «начальн.угол в град.»; у1: у=у1*Р1/180 Input «шаг по epeMeuu»; dt t=0: w=0

l:w=w-g*Sin (y)*dt/L: y=y+w*dt If y<0 then Goto 2 t=t+dt Goto 1.

2:Print yl, t*4 End

Точность определения периода зависит, как всегда, от величины шага dt. Чем шаг меньше, тем больше цифр после точки будут правильными, но машина будет считать дольше.

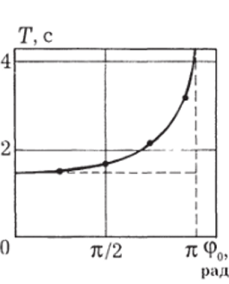
График зависимости Т (ф₀) приведен на рисунке 2.44. При ф₀, стремящемся к 180°, период Т стремится к бесконечности. р_ис 2 44.