Интегральные уравнения. 
Численные методы

ИНТЕРАЛЬНЫМ называют уравнение, в котором неизвестная функция и (х) находится под знаком интеграла. Одномерное нелинейное интегральное уравнение имеет вид.

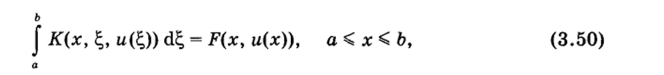
где ядро К (х, ц) и правая часть F (x, и) — заданные функции.

К интегральным уравнениям приводят многие физические задачи. Так, задача восстановления переданного радиосигнала u (t) по принятому сигналу /(*) сводится к решению интегрального уравнения типа свертки

где ядро K (t — т) зависит от свойств приемной аппаратуры и среды, через которую проходит сигнал. К интегральным уравнениям сводятся также задачи образования заданной новой фазы при конденсации и кристаллизации.

Интегральные уравнения в некоторых отношениях удобнее дифференциальных. Во-первых, интегральное уравнение содержит в себе полную постановку задачи. Например, интегральное уравнение.

эквивалентно задаче Коши для дифференциального уравнения.

однако для уравнения (3.52) не требуется задавать никаких дополнительных условий, начальных или граничных.

Во-вторых, в интегральных уравнениях переход от одной переменной ко многим является естественным. Так, многомерным аналогом уравнения (3.50) является уравнение.

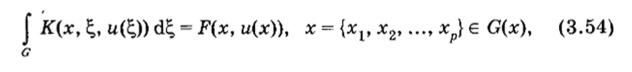
отличающееся от уравнения (3.50) только тем, что интегрирование проводится по многомерной области G. Поскольку оба уравнения не требуют дополнительных условий и полностью определяют задачу, аналогия является полной. Тем самым теоретическое обоснование постановок и методов решения одномерных задач непосредственно обобщается на случай многих переменных.

Наоборот, в дифференциальных уравнениях переход от одной переменной к нескольким, т. е. от обыкновенных дифференциальных уравнений к уравнениям в частных производных, является принципиальным усложнением, приводит к новым постановкам задач и требует новых методов для их обоснования.

Далее мы ограничимся рассмотрением одномерного уравнения (3.50) и некоторых его частных случаев.

| Линейные задачи Лучше всего изучены уравнения, в которые неизвестная функция и (х) входит линейно. Их можно записать в виде.

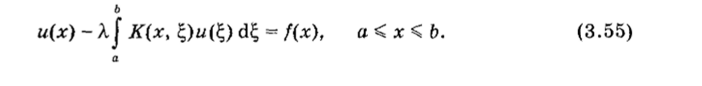
ФРЕДГОЛЬМ ЭРИК ИВАР (Fredholm Erik Ivar; 1866- 1927) — шведский математик, известный своими исследованиями по теории линейных интегральных уравнений. Им разработаны общие методы решения некоторых их видов (уравнений Фредгольма).

Такое уравнение называют УРАВНЕНИЕМ ФРЕДГОЛЬМА ВТОРОГО РОДА: ядро К (х, этого уравнения определено на квадрате.

а < х < Ь, а <? < Ь.

Если ядро К (х, ?) отлично от нуля только на треугольнике а <? < х < Ь, т. е. К (х, !;) = О при х < ?, то уравнение (3.55) переходит в УРАВНЕНИЕ ВОЛЬТЕРРА ВТОРОГО РОДА.

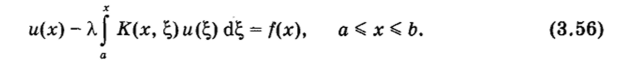
Это уравнение теоретически исследовать или численно решить много проще, чем уравнение Фредгольма.

Если в уравнениях (3.55) и (3.56) отбросить член и (х), оставив только ц (^) под знаком интеграла, то получим уравнения Фредгольма и Вольтерра первого рода. Задачи для уравнений первого рода являются некорректно поставленными. Для уравнений второго рода задачи корректно поставлены; остановимся на этих задачах. Изложим численный метод, позволяющий получать решение одномерных задач с хорошей точностью, а двумерных — с удовлетворительной. Он рассчитан на применение компьютера, хотя оценки с небольшим числом узлов сетки можно производить вручную.

Рассмотрим одномерное нелинейное уравнение (3.50). Возьмем на отрезке [а, Ь] какую-либо квадратную формулу*, например, линейную формулу с узлами х_п и весами с_п

Введем в квадрате [а < х < Ь, а < % < 6] сетку [х_п, ?_т], где х_п и ?_т являются узлами формулы (3.57). Заменяя интеграл в уравнении (3.50) суммой (3.57), получим систему алгебраических уравнений для определения приближенных значений в узлах ~ и (х")

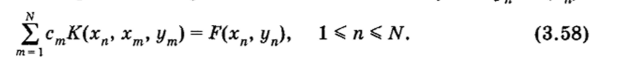
Эту систему целесообразно решать методом Ньютона.

* Нелинейные квадратурные формулы почти никогда не используются.

ВОЛЬТЕРРА ВИТО (Volterra Vito; 1860—1940) — итальянский математик. Наиболее известны его работы в областях дифференциальных уравнений с частными производными, интегральных (уравнения Вольтерра) и интегро-дифференциальных уравнений, функционального анализа и теории упругости.

Неоднородное уравнение Фредгольма (3.55) приводит к линейной неоднородной алгебраической системе.

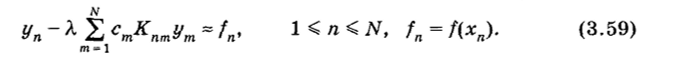
Разностное решение легко определяется методом исключения Гаусса.

Уравнение Волыперра (3.56) получают из уравнения Фредгольма (3.55), полагая К (х, ^) = 0 при х < lq. Алгебраическая система (3.59) становится при этом треугольной.

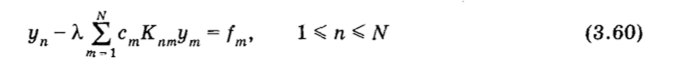
и решается обратным ходом метода Гаусса всего за (3/2)N² действий. Поэтому здесь объем вычислений остается умеренным даже при N — 1000, что позволяет проводить расчеты с очень высокой точностью.

j Выбор квадратурной формулы Большинство задач приходится решать, используя сравнительно небольшое число узлов N. Поэтому для получения хорошей точности целесообразно выбирать квадратурные формулы высокого порядка точности, разумеется, если К (х, q) и f (x) имеют достаточное число непрерывных производных.

Обычно наилучшие результаты для достаточно гладких решений дают квадратурные формулы Гаусса или Гаусса — Кристоффеля; при числе узлов k их порядок точности р = 2k. Можно также использовать простейшую формулу трапеций, последовательно сгущая сетки вдвое от N₁ — 2 до N_k = 2* и уточняя решение способом Рунге; это также дает результат с порядком точности* р — 2fe, но требует использования существенно большего числа узлов, чем в формулах Гаусса.

* Каждая лишняя сетка позволяет повысить порядок точности на 2, поскольку погрешность формулы трапеций разлагается по четным степеням шага Л.

КРИСТОФФЕЛЬ ЭЛЬВИН БРУНО (Christoffel Elwin Bruno; 1829—1900) — немецкий математик, известный работами в области теории функций, теории дифференциальных уравнений с частными производными, теории инвариантов алгебраических форм и теории дифференциальных квадратичных форм, где им введен (1869) символ, носящий его имя. Этот символ используется, в частности, при записи элементов тензора кривизны, который иногда называют вследствие этого тензором Римана — Кристоффеля.