Методы сквозного счета

В задачах механики сплошных сред приходится иметь дело с течениями, в которых возникают поверхности сильного разрыва такие, как ударные волны, центрированные волны разрежения, поверхности контактного разрыва. На этих поверхностях терпят разрыв функции и их производные. При расчете таких течений приходится либо явно выделять эти поверхности, используя законы сохранения, либо строить специальные методы решения, называемые методами сквозного счета, в которых a priori неиз;

ГОДУНбВ СЕРГЕЙ КОНСТАНТИНОВИЧ (1929) — математик, чьи основные исследования относятся к теории чисел, теории функций комплексного переменного, теории дифференциальных уравнений, численным методам линейной алгебры, приближенным и численным методам прикладной математики. Г. разработал разностные методы решения нестационарных задач.

вестные поверхности разрыва явно не выделяются и просчитываются насквозь вместе с областями непрерывного течения.

Весьма эффективным и красивым методом сквозного счета является МЕТОД ГОДУНОВА. В основе метода Годунова лежат две идеи. Первая состоит в использовании при построении разностной схемы точных решений с кусочно-постоянными начальными данными. Для гиперболических уравнений такими точными решениями являются совокупности сравнительно простых и независимых решений задачи о распаде произвольного разрыва.

Вторая идея состоит в использовании гибких и деформирующихся разностных сеток, связанных с поверхностями разрывов и выделяемых при расчете начальной стадии. Рассмотрим применение метода Годунова при решении задачи Коши для уравнений акустики:

где U и Р — соответственно возмущения скорости и давления в акустической волне, а₀ и р₀— скорость звука и плотность в невозмущенном газе. Используя инвариант Римана I_± = Р ± a_Qp₀U и обозначив через fug произвольные функции, определяемые из начальных условий, для уравнений (4.67) можно записать общее решение.

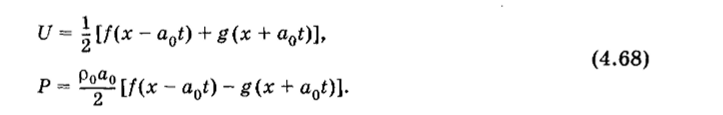
Построим с использованием (4.68) решение простейшей задачи о распаде. Обозначим через ?/, U_u, P_v Р_ц некоторые постоян;

РЙМАН ГЕОРГ ФРИДРИХ БЕРНХАРД (Riemann Georg Friedrich Bernhard; 1826—1866) — немецкий математик. Р. дал оригинальное построение теории аналитических функций, положил начало геометрическому направлению в ней, выдвинул ряд основных идей новой науки — топологии. Труды Р. посвящены разработке неэвклидовой геометрии, рассматривавшейся им как учение о непрерывных л-мерных многообразиях. Таким образом, им были обобщены идеи Гаусса по внутренней геометрии поверхности, Гаусса — чьи лекции он слушал, будучи студентом Геттингенского университета. Работы Р. оказали глубокое влияние на развитие математики второй половины XIX—XX вв.

ные такие, что U_t * С/_н и Р₁ А Р_ц. Пусть в момент t = О заданы начальные условия.

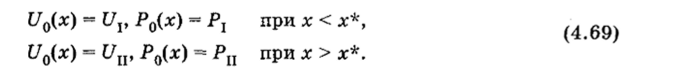
Начальные условия (4.69) таковы, что имеет место произвольный разрыв функций U и Р в точке х^[1], который с течением времени каким-то образом трансформируется в пространстве х, t. Такая задача и называется задачей о распаде произвольного разрыва. Построим ее решение, используя свойства инвариантов Римана. Поскольку инвариант Римана 1₊ постоянен вдоль характеристики х — a₀t = const, а инвариант 1_ постоянен вдоль характеристики х + a₀t ~ const, приходим к структуре решения, изображенной на рис. 4.19. Решение задачи о распаде разрыва имеет вид.

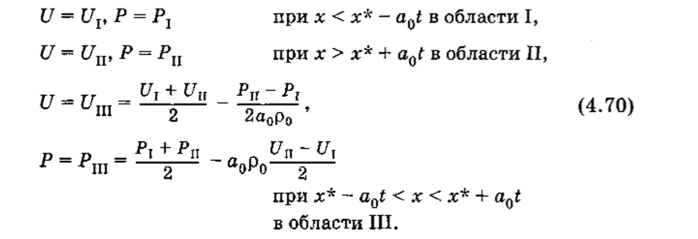
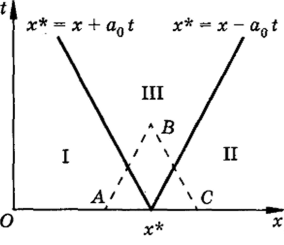
Эти области изображены на рис. 4.19^[1].

Построенные таким образом функции Щх, t) и Р (х, t) имеют разрывы вдоль характеристик х + a_Qt = х^[1] и х — a_Qt ~ х^[1], разделяющих области I, П и III. Поскольку функции U и Р не являются непрерывными, то примем, что полученное решение является обобщенным решением задачи о распаде разрыва.

Перейдем к построению разностной схемы метода Годунова.

Рис. 4.19 ностной схемы метода Годунова.

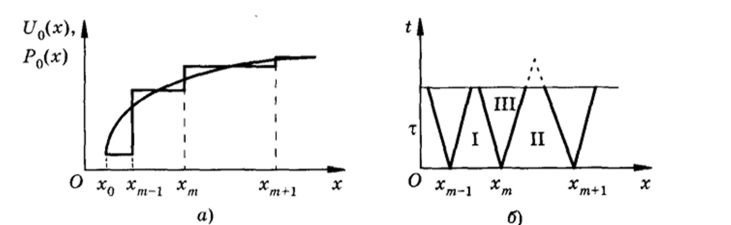
Рис. 4.20.

Пусть в момент времени t — О заданы непрерывные функции U₀(x) и Р₀(х). Заменим область непрерывного изменения аргумента дискретным множеством точек — разностной сеткой, узлы которой обозначим через х_т. Расстояние между соседними узлами является шагом разностной сетки. Примем, что между точка- ^{ми х}т — 1 ^{и х}т Функции U и Р постоянны. Такое предположение эквивалентно тому, что непрерывные функции U_Q(x) и Р₀(х) заменены некоторыми кусочно-постоянными функциями, сохраняющими постоянные значения между узлами разностной сетки (рис. 4.20, а).

Значения функций U (x) и Р (х) между узлами разностной сетки обозначим через U_m _ _½ и Р_т_ _½, присвоив соответствующему слою полуцелый индекс (т — ½).

На границе между слоями возникает распад разрыва. В результате в каждом узле сетки образуются звуковые волны, распространяющиеся вправо и влево со скоростью звука а₀. Через некоторый отрезок времени т структура решения примет вид, представленный на рис. 4.20, б. Согласно формулам (4.70) решение в окрестности точки х_т будет.

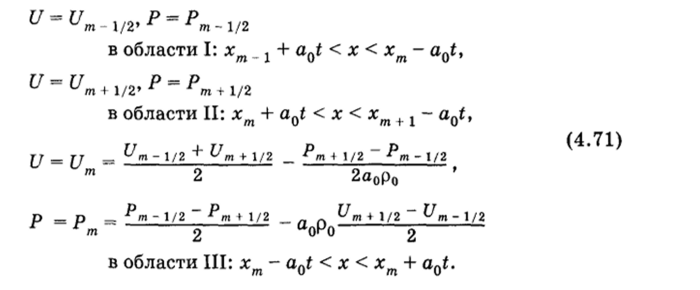
Здесь через U_п и Р_т обозначены значения, возникающие при распаде разрыва в узле т.

Изображенная на рис. 4.20 структура решения сохранится до тех пор, пока звуковые волны, вышедшие из соседних узлов, не встретятся между собой. После этого ее нужно перестроить заново, и даже в случае равномерной сетки эта процедура оказывается чрезвычайно громоздкой.

В связи с этим предлагается следующий способ построения решения в момент времени t = т. Заменим решение (4.71) другим решением таким, которое имеет ту же структуру, что и в начальный момент t = 0. Приближенно примем, что решение при t ~ т также кусочно-постоянно внутри интервалов, ограниченных прежними узлами сетки х_п. Новые средние значения этих функций при t = т между узлами х_т_ _L и х_т обозначим через U^m ~ ^½ и.

рт — ½.

Эти величины можно определить по формулам.

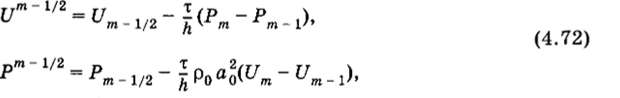
в которых значения U и Р в правой части определяются по формулам (4.61) для точек ии/п-1 соответственно.

Действительно, рассмотрим законы сохранения в интегральной форме для первого и второго уравнений (4.66), которые следуют из формулы Грина.

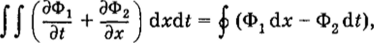
в которой Ф₁ •= U или = Р и Ф₂ = Р/р₀ или Ф₂ = р₀а^и для перво го и второго уравнений соответственно. Имеем.

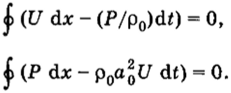
Запишем эти соотношения для прямоугольной ячейки в плоскости (jc, t), ограниченной прямыми х = х_т _ ₁₍ х = х_т, t = О, t = х. Имеем ГРИН ДЖОРДЖ (Green George-, 1793—1841) — английский математик. Г. нашел соотношение межд> интегралами по объему и поверхности, ограничивающей объем. Он ввел термин потенциал и развил теорию электричества и магнетизма.

Так как U (x, 0) и Р (х, 0) постоянны на интервале от х_т _ _г до х_т и равны соответственно U_т _ _½ и Р_т _ _½ и, аналогично, TJ (x, т) и Р (х, т) равны U^m «^½ и Р^т~ ^½, а на левой и правой сторонах ячейки U (x, t) и Р (х, t) принимают постоянные значения U_т _

U_т и Р_т_ j, Р_т соответственно, которые вырабатываются при распаде разрыва в узлах т и (т — 1), то из формул (4.73) следуют соотношения (4.72).

Формулы (4.73) справедливы до тех пор, пока не происходит пересечения звуковых волн, приходящих из соседних ячеек. Это имеет место при т < Л/а₀, что, как видно, является условием Куранта — Фридрихса — Леви. Описанная разностная схема перехода с одного временного слоя на другой имеет первый порядок точности по т и h.

• [1] Формулы для области III в соотношениях (4.70) получены из рассмотрения инварианта Римана на характеристиках АВ и ВС. Имеем ?^ш + аоРо^ш ~ ^ aoPo^i Ha ~ аоРо^ш = рп ~ аоРо^н на ВС. Складывая и вычитая эти соотношения, получим выражения в формулах (4.70).
• [2] Формулы для области III в соотношениях (4.70) получены из рассмотрения инварианта Римана на характеристиках АВ и ВС. Имеем ?^ш + аоРо^ш ~ ^ aoPo^i Ha ~ аоРо^ш = рп ~ аоРо^н на ВС. Складывая и вычитая эти соотношения, получим выражения в формулах (4.70).
• [3] Формулы для области III в соотношениях (4.70) получены из рассмотрения инварианта Римана на характеристиках АВ и ВС. Имеем ?^ш + аоРо^ш ~ ^ aoPo^i Ha ~ аоРо^ш = рп ~ аоРо^н на ВС. Складывая и вычитая эти соотношения, получим выражения в формулах (4.70).
• [4] Формулы для области III в соотношениях (4.70) получены из рассмотрения инварианта Римана на характеристиках АВ и ВС. Имеем ?^ш + аоРо^ш ~ ^ aoPo^i Ha ~ аоРо^ш = рп ~ аоРо^н на ВС. Складывая и вычитая эти соотношения, получим выражения в формулах (4.70).