Винеровский случайный процесс

Случайный процесс X (w, ?), определенный на промежутке | ?₀; +°°) называется винеровским случайным процессом, если выполняются следующие условия:

• 1) Х (со, ?₀) = х, где х — некоторое заданное число;
• 2) приращения случайного процесса Х (ш, ?) независимы;
• 3) приращение Х (со, t) — Х (со, s), t > s, распределено нормально с математическим ожиданием 0 и дисперсией t — s;
• 4) все траектории случайного процесса Х (со, ?) непрерывны на промежутке [?₀; +°°).

В большинстве приложений предполагается, что начальное значение винеровского процесса Х (со, 0) = 0 и начальное время ?₀ = 0. В этом случае винеровский процесс называется стандартным. В дальнейшем будем также придерживаться указанных предположений и рассматривать только стандартный вариант винеровского процесса. Кроме того, в силу особой важности винеровского случайного процесса в построении различных моделей ценообразования на финансовых рынках для него будем использовать отдельное обозначение Щсо, ?), или W_L — для траекторий этого процесса. Отметим важное свойство винеровского процесса, а именно, справедливость соотношения.

Последняя зависимость означает выполнение условия М 1 —> 0.

ч а? ,.

при dt —> 0.

Винеровский процесс является физико-математической моделью, в частности, перемещения частичек цветочной пыльцы, помещенных в жидкость. Хаотический, или беспорядочный, характер такого перемещения впервые в начале XIX в. отметил известный ботаник Р. Броун. Поэтому винеровский случайный процесс часто называют броуновским движением. Броуновское движение как математический объект используется в работах А. Эйнштейна, относящихся к началу XX в. Строгую математическую теорию броуновского движения, его меру в функциональном пространстве построил Н. Винер (Wiener), в честь которого и назван соответствующий случайный процесс.

В подпараграфе 2.1.1 отмечено, что винеровский процесс может быть построен из случайных блужданий с помощью некоторого предельного перехода, и фактически в таком виде модель броуновского движения была построена Л. Башелье в 1900 г. при описании им изменения цен акций и других финансовых активов. Рассмотрим данный вопрос более подробно. Пусть — последовательность независимых одинаково распределенных случайных величин, принимающих значения +1 и -1 с вероятностями ½. Образуем на множестве [0; +) для каждого, А > 0 процесс Х (^д) = (Xf)_t>₀ с кусочно-постоянными траекториями.

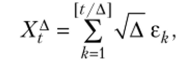
где [t/A — целая часть выражения t/A.

По процессам Xможно также образовать случайные процессы у (Д) =(К_Г^Л)_Г>₀ с непрерывными траекториями, полагая выполнение следующей зависимости: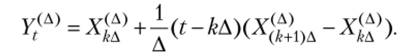

Применяя центральную предельную теорему, можно получить¹, что для любых ?_1? …, t_k, k > 1, конечномерные распределения (Х^…, Х^⁾) и сходятся к конечномерным распределениям (W^,…, W_tk),.

где (W_t)_r>₀ ^— стандартный винеровский процесс.

Приведем основные свойства винеровского процесса.

• 1. Сечение винеровского процесса U⁷Xco) является нормально распределенной случайной величиной с нулевым математическим ожиданием и дисперсией t> т. е. ~ Л^(0, t).
• 2. Если WXco) ^и ^vC⁰³)' t < s, являются сечениями винеровского процесса, то cov (WXw), iyXco)) ⁼ *•
• 3. Плотность совместного распределения вероятностей системы сечений стандартного винеровского случайного процесса (W_t{ (со),…, W_t (со)), где О _{<… < t_k, имеет вид

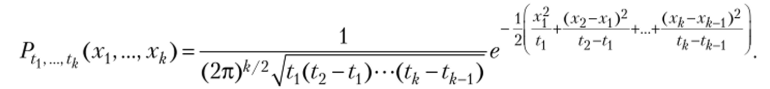
Ширяев Л. II. Вероятность. 2-е изд., перераб. и доп. М.: Наука. 1989.

4. Винеровский процесс является однородным.

Для моделирования траекторий винеровского случайного процесса W, на заданном промежутке времени [0; У] можно использовать метод МонтеКарло^[1]. На рис. 2.4 приведена одна из возможных траекторий стандартного винеровского процесса на интервале [0; 1].

Рис. 2.4. Траектория стандартного винеровского процесса на интервале [0; 1]

Чисто винеровский процесс редко используется для моделирования динамики финансовых показателей (например, цен акций, облигаций, значений индексов и т. д.). Однако на его основе строятся почти все случайные процессы, используемые в современной финансовой математике.

При конструктивном способе задания случайных последовательностей г = (/-«), описывающих динамику доходностей.

от, например, вложений в акции, стоимость которых на момент времени п равна Р_п, обычно предполагается в соответствующих моделях, что имеется некоторая базовая последовательность дискретных случайных величин е = (е"), являющихся источником случайности и порождающая в свою очередь последовательность г = (г_п). При этом, как правило, считается, что указанная последовательность является белым шумом, что в данном случае подразумевает независимость и одинаковое нормальное распределение указанных величин, обладающих нулевым математическим ожиданием. Выбор такой последовательности в качестве базовой отвечает естественному желанию строить сложные объекты (каковыми являются, например, процессы ценообразования на финансовые активы) на основе простых.

Последовательность? = (е") действительно может считаться просто устроенной, поскольку она состоит из независимых одинаково распределенных случайных величин со стандартным нормальным распределением. В случае непрерывных моделей ценообразования аналогичную роль базовой структуры играет как раз винеровский случайный процесс. Одним из первых подробно роль винеровского процесса (броуновского движения) в моделировании рынка ценных бумаг рассмотрел М. Осборн (Osborne) в своей статье, опубликованной в 1959^[2].

• [1] Лобанов А. А., Чугунов А. В. Энциклопедия финансового риск-менеджмента. М.: Альпина Паблишер, 2003.
• [2] Osborne М. F. М. Brownian motion in the stock market // Operations Research. March-April 1959. Vol. 7. P. 145−178.