Пример анализа устойчивости САР третьего порядка

Приведем пример анализа устойчивости системы автоматического регулирования третьего порядка, структурная схема которой приведена на рис. 3.3. Постоянные времени звеньев имеют следующие параметры: Т_х = 0,01 с, Т₂ = 0,02 с, Г3 = 0,05 с. Коэффициент усиления k = k_xk₂k₃ разомкнутой системы принимает два значения: 10 и 30. Требуется проанализировать устойчивость системы в этих двух случаях. Левая часть характеристического уравнения САР является знаменателем передаточной функции замкнутой системы в соответствии с формулой (3.38). На рис. 3.7 знаменатели передаточных функций записаны как полиномы Fl (x) и F2(x) для двух случаев коэффициента усиления. Корни характеристического уравнения в интегрированном пакете MathCad находятся с помощью функции polyroots. Эта функция находит корни полинома, коэффициенты которого находятся в векторе-столбце F1.

Замечание 3.2.

В интегрированном пакете MathCad индексные переменные а₀, а_и а₂, Т, Т₂, F, F₂, и т. д., которые воспринимаются в программе как элементы массивов, ради удобства заменены обычными переменными со строчными (не подстрочными) индексами аО, al, а2, Tl, Т2, FI, F2 и т. д.

Рис. 3.7. Нахождение корней характеристического уравнения САР третьего порядка и определение устойчивости системы в интегрированном пакете MathCad

Приравняем нулю определитель Д₂ высшего порядка (п — 1 =3−1=2), считая значения постоянных времени Т_{, Т₂ и Т₃ заданными, а коэффициент усиления k неизвестным. В результате получим уравнение, соответствующее нахождению системы на границе устойчивости:

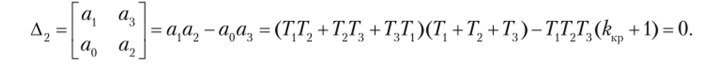
Из этого уравнения находим критическое значение коэффициента усиления /е_кр = 12,6.

Запасом устойчивости системы по амплитуде Aк называют величину, показывающую, во сколько раз необходимо увеличить значение коэффициента усиления системы при неизменных значениях всех остальных ее параметров, чтобы устойчивая система оказалась на границе устойчивости. Для устойчивой системы с коэффициентом усиления k = 10 запас устойчивости по амплитуде

Проверим правильность полученных результатов с помощью моделирования структурной схемы САР, показанной на рис. 3.3, в пакете MATLAB, Simulink. Модель системы, собранная с помощью трех блоков передаточных функций Transfer Fen, приведена на рис. 3.8. Коэффициент усиления разомкнутой системы принят равным 10. С помощью таймера задается режим, когда нагрузка возрастает скачком. Как следует из рис. 3.8, переходный процесс носит характер затухающих колебаний. Система устойчива. Для быстрой ликвидации большого начального рассогласования скорость нарастания регулируемой величины в начале процесса максимальная. Однако при этом система по инерции проходит сравнительно далеко за требуемое значение. Такое отклонение регулируемой величины в сторону, противоположную отклонению, называют перерегулированием. Технические требования к системе предусматривают ограничение перерегулирования.

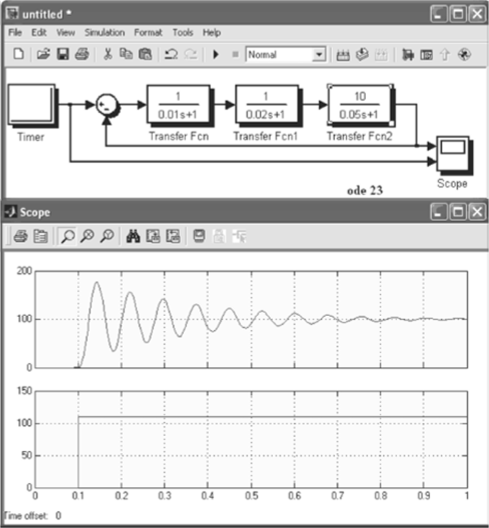
Рис. 3.8. Переходный процесс в САР с тремя апериодическими звеньями, к = 10.

На рис. 3.9 приведен переходный процесс в той же САР с тем же входным воздействием, но с коэффициентом усиления к = 12,56. Как было показано выше, это значение коэффициента является критическим. При этом значении коэффициента усиления к в переходном процессе возникают незатухающие колебания и система оказывается на грани устойчивости. Если коэффициент усиления будет больше, чем 12,56, то колебания будут расходящимися и система станет неустойчивой. Читателю предлагается самому убедиться в этом, исследуя схему на рис. 3.8 с коэффициентом усиления к = 15.

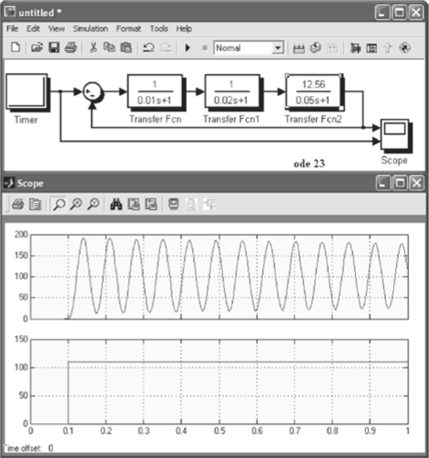
Рис. 3−9- Переходный процесс в САР с тремя апериодическими звеньями, к = 12,56.

При использовании критерия Найквиста воспользуемся передаточной функцией разомкнутой системы, которая выражается формулой (3.37) при замене р = jar.

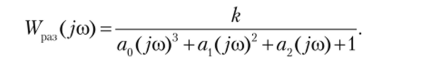
Построим по этой формуле амплитудно-фазовые частотные характеристики также для двух значений коэффициента усиления. Кривая 1 на рис. 3.10 построена для коэффициента усиления к = 10, а кривая 2 — для k = 30. Первая кривая не охватывает точку с координатами (—1; у0), поэтому система устойчива. Во втором случае кривая 2 охватывает точку с координатами (—1;_/0), и система неустойчива. На рис. 3.10, а АФЧХ показаны полностью, а на рис. 3.10, б в крупном масштабе показаны участки АФЧХ вблизи точки с координатами (-1;уО). На рис. 3.10, б хорошо видно, что кривая 1 не охватывает точку с координатами (-1; у’О), а кривая 2 охватывает ее.

На рис. 3.11 приведены годографы Михайлова для исследуемой схемы. Для их построения использовано характеристическое уравнение замкнутой системы, в котором оператор р заменяется оператором уса, т. е. полином.

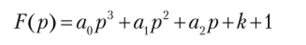
заменялся полиномом.

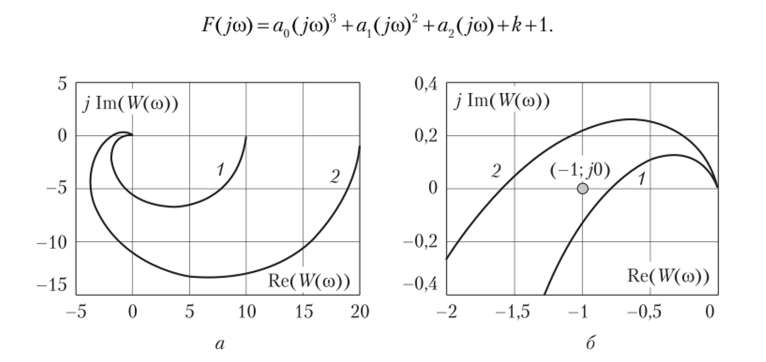
Рис. 3.10. Амплитудно-фазовые частотные характеристики САР:

1 — САР устойчива; 2 — САР неустойчива Годограф этого полинома строился на комплексной плоскости (рис. 3.11). Кривая 1 построена для коэффициента усиления k = 10, а кривая 2 — для k = 30.

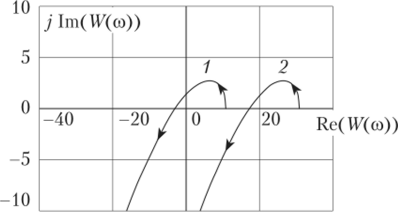
Рис. 3.11. Годографы Михайлова:

1 — САР устойчива; 2 — САР неустойчива Согласно критерию Михайлова годограф устойчивой САР третьего порядка должен проходить против часовой стрелки через три квадранта. Из рис. 3.11 следует, что кривая 1 проходит через три квадранта и система устойчива. Кривая 2 проходит только через два квадранта. Следовательно, в этом случае система неустойчива.

На рис. 3.12 показаны АФЧХ замкнутой системы для тех же значений k, равных 10 и 30.

В первом случае кривая идет по часовой стрелке и проходит три квадранта, а во втором она движется против часовой стрелки и проходит два квадранта.

Результаты проведенного выше анализа подтверждаются расчетом в интегрированном пакете MathCad переходного процесса в рассматриваемой САР при двух значениях коэффициента усиления (рис. 3.13 и 3.14). Расчет произведен путем численного решения системы дифференциальных уравнений методом Рунге — Кутта четвертого порядка. Как следует из рис. 3.13 и 3.14, при k = 10 (k_x = 2, k₂ = 2, k₃ = 2,5) система устойчива, а при k = 30 (k_{ =2, k₂ = 3, k₃ = 5) — неустойчива.

Рис. 3.12. Амплитудно-фазовая частотная характеристика замкнутой системы:

1 — при к = 10 система устойчива; 2 — при к = 30 система неустойчива При решении дифференциальных уравнений вместо переменныхх₂,х₃, у были введены следующие машинные (компьютерные) переменные: х₀, х, х₂. Задающий входной сигнал обозначен как Xbx (t).

Таким образом, была решена система следующих дифференциальных уравнений.

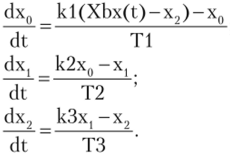
В этих уравнениях компьютерные переменные с индексами являются элементами массива.

На рис. 3.15 приведен расчет операторным методом в интегрированном пакете MathCad переходного процесса в устойчивой САР третьего порядка, показанной на рис. 3.3, при ступенчатом входном сигнале. Коэффициент усиления разомкнутой системы k = 10. На рис. 3.15 коэффициент усиления обозначен прописной буквой К.

Строчная буква k используется для индекса корней характеристического уравнения р_к. Скачкообразное входное воздействие изображается в операторной форме как Х (р) = х/р = 110/р. В соответствии с формулой (3.38) изображение выходного сигнала будет иметь вид.

Рис. 3.13. Расчет переходного процесса в устойчивой CAP (k = 10).

Напомним, что в интегрированном пакете MathCad у величин, не являющихся элементами массива, подстрочные индексы заменяются на строчные (а₀ = аО, Fj = F1 и т. д.). Четыре корня характеристического уравнения F2(p) = 0 были найдены ранее с помощью функции polyroots (см. рис. 3.7) и па рис. 3.15 эти корни заданы в виде вектора р. Один из корней равен нулю. Второй корень вещественный отрицательный, и два корня сопряженные комплексные с отрицательной действительной частью. По характеру корней можно сделать заключение о том, что система устойчива. Для перехода от изображения к оригиналу использована теорема разложения, согласно которой переходный процесс определяется суммой четырех экспонент (по числу корней характеристического уравнения). Для нахождения производной по оператору р от знаменателя F2(p) использован оператор векторизации вектора [Ctrl]+[-]. Этот оператор говорит о том, что операция дифференцирования производится с каждым элементом вектора, соответствующим данному корню характеристического уравнения.

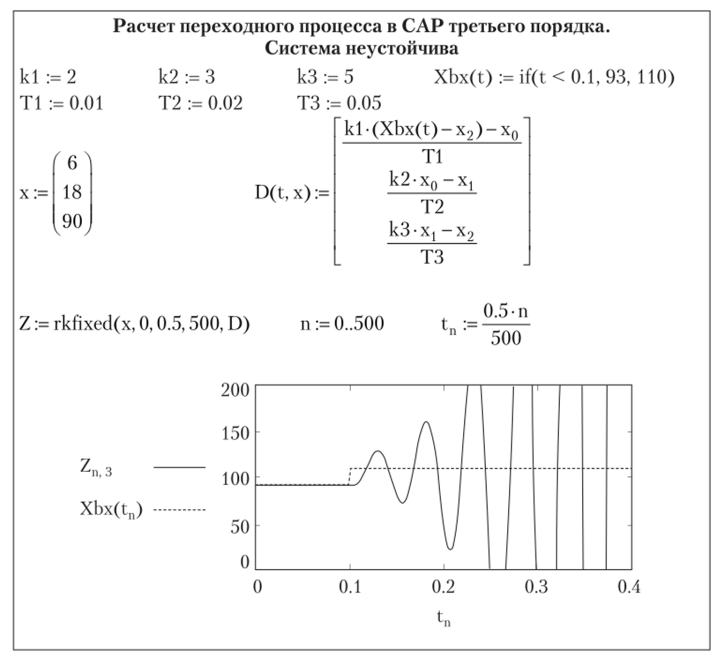
Рис. 3.14. Расчет переходного процесса в неустойчивой CAP (k = 30).

На рис. 3.16 показан расчет операторным методом в интегрированном пакете MathCad переходного процесса в той же САР третьего порядка при ступенчатом входном сигнале меньшего значения, но при другом значении коэффициента усиления: k = 30 (в MathCad К = 30). В этом случае действительные части комплексных корней, найденные ранее на рис. 3.7, положительные, что говорит о неустойчивости системы. Это показывает и график на рис. 3.16.

График переходного процесса позволяет оценить качество исследуемой системы при скачкообразном воздействии на нее. Чтобы построить такой 1-рафик с помощью классического или операторного методов, необходимо найти корни характеристического уравнения. На практике бывает необходимо дать примерную оценку качества системы по ее корням, нс прибегая к построению графика. Рассмотрим, как сделать такие оценки по корням характеристического уравнения. Из рис. 3.7 следует, что при k = 10 имеются три корня: один вещественный отрицательный и два сопряженных комплексных корня с отрицательными вещественными частями: -8±(о = -3,781±82,204у. Следовательно, процесс носит колебательный характер с затуханием.

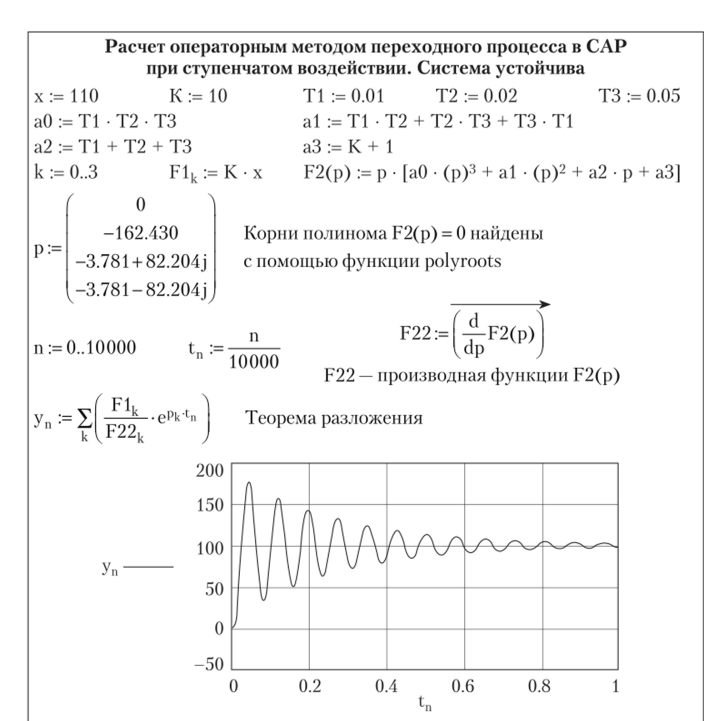
Рис. 3.15. Расчет операторным методом в интегрированном пакете MathCad переходного процесса в устойчивой САР.

Все три составляющие переходного процесса с течением времени t затухают по экспоненциальному закону и становятся равными нулю. Быстрее затухают те составляющие переходной функции, у которых вещественная часть корня по абсолютной величине наибольшая. Таким образом, из анализа скорости затухания слагаемых переходной функции можно выделить те корни, которые определяют время Т_1Щ) переходного процесса.

В рассматриваемом примере скорость затухания будет наименьшей у комплексных составляющих, у которых коэффициент затухания б = 3,781. Этот коэффициент затухания будет доминирующим. Можно считать, что экспоненциальная составляющая полностью затухает, когда показатель степени у экспоненты равен -4. Отсюда время переходного процесса.

что и подтверждает рис. 3.15.

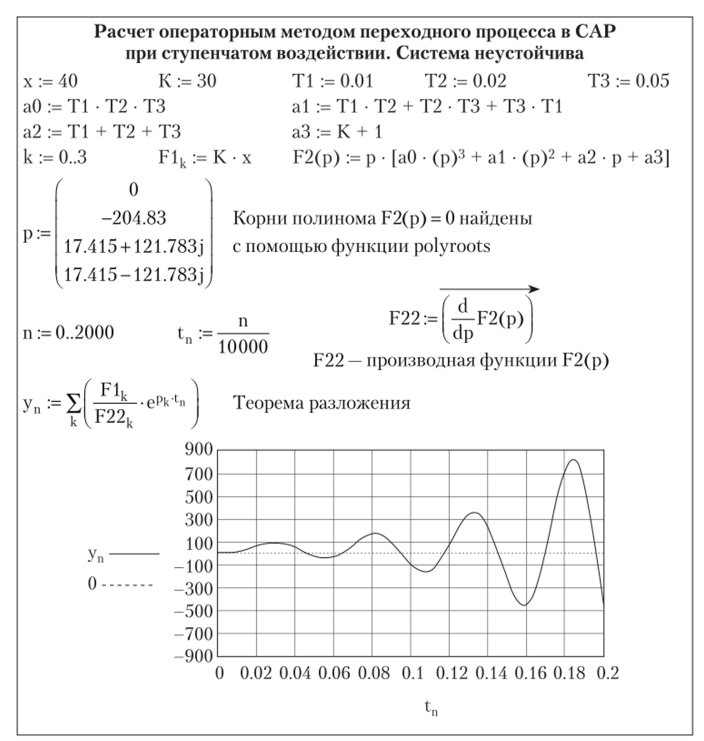
Рис. 3.16. Расчет операторным методом в интегрированном пакете MathCad переходного процесса в неустойчивой САР.

Период колебаний Т_кол примерно можно оценить по формуле.

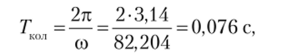
что также подтверждает рис. 3.15.

Подводя итог обсуждению различных способов анализа переходных процессов в САР, можно сделать следующие выводы. При современном уровне развития компьютерной техники наиболее рациональным способом оценки переходных процессов является решение системы дифференциальных уравнений численным методом Рунге — Кутта в интегрированном пакете MathCad. Достоинством этого метода является то, что при расчете определяется не только одна выходная величина, но и все промежуточные величины, входящие в систему дифференциальных уравнений. В результате решения можно построить временные зависимости выходных величин всех звеньев САР. На входе схемы можно задать любое воздействие, описав его математически с учетом нелинейных зависимостей отдельных звеньев САР.

Заметим, что нелинейная САР может быть устойчива при небольших отклонениях (устойчива в «малом») и неустойчива при больших отклонениях (неустойчива в «большом»), что иллюстрирует рис. 3.17.

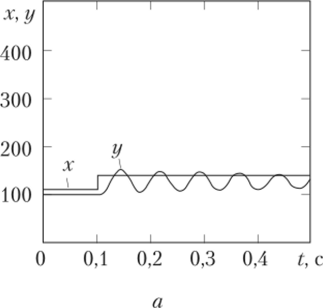
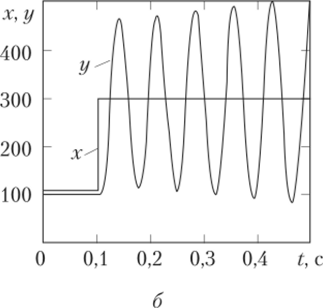
Рис. 3.17. Переходный процесс в нелинейной системе, устойчивой в «малом» (а) и неустойчивой в «большом» (б).

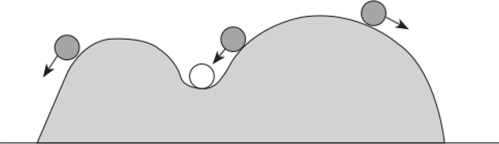
Рис. 3.18. САР устойчивая в «малом» и неустойчивая в «большом».

Рис. 3.18 дает графическую интерпретацию устойчивости в «малом» и неустойчивости в «большом».