Метод сопряженных градиентов Понятие сопряженности векторов

Если целевая функция — выпуклая квадратичная функция, принадлежащая пространству R", то для нахождения экстремума методом сопряженных градиентов требуется не более п итераций. Конечное число шагов — большое достижение для практики. Это обеспечивается поворотом главных осей линий уровня таким образом, чтобы одна из главных осей прошла через точку экстремума. Свойство сопряженности векторов… Читать ещё >
Метод сопряженных градиентов Понятие сопряженности векторов (реферат, курсовая, диплом, контрольная)
д2 ~к
В разделе 3 была введена матрица Гессе Н = ° ^ -, элементы.
дх.дх.
которой для «-мерного пространства R, имеют вид.
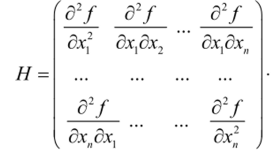
Пусть имеем два направления, которые характеризуются векторами.
—О —I.
Р и Р .
—1 —о Если скалярное произведение (Р, Р) = (), то векторы ортогональны, т. е. взаимно перпендикулярны.
— I —о Если скалярное произведение (Р, Н Р) = (), то векторы называются сопряженными относительно матрицы Я. Здесь Я — положительно определенная квадратная матрица.
Приведенные определения имеют определенную геометрическую иллюстрацию, приведенную на рис. 3.16. Матрица Я, умноженная на.
—О ^.
вектор Р, изменяет его длину и поворачивает на некоторый угол. И этот новый полученный вектор ортогонален к вектору Р .
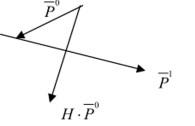
Рис. 3.16.
Свойство сопряженности векторов используется в методе сопряженных градиентов, который отличается от метода наискорейшего спуска только выбором направления уменьшения функции на каждом шаге. Вместо вектораV/(x*) метод использует вектор -Рк.
Формула метода сопряженных градиентов 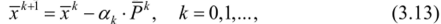 имеет вид где х° е R" — вектор начальных приближений. Шаг ак выбирается аналогично (3.10) из решения задачи одномерной оптимизации:
имеет вид где х° е R" — вектор начальных приближений. Шаг ак выбирается аналогично (3.10) из решения задачи одномерной оптимизации:
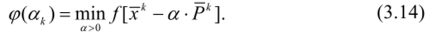
Направление спуска Рк определяется по формуле 
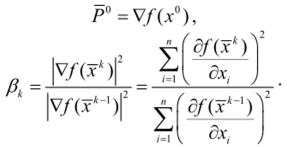
Векторы Pv Р2, Р2 являются сопряженными.
где.
Замечания
- 1. В данном методе направление спуска определяет не только анти-
- —к —Л-1
градиент -Vf (x), но и направление спуска на предыдущем шаге Р .
- 2. Для снижения влияния накапливающихся ошибок вычисления рекомендуется через п шагов поиска обнулять длину шага Д, = 0.
- 3. Если целевая функция — выпуклая квадратичная функция, принадлежащая пространству R", то для нахождения экстремума методом сопряженных градиентов требуется не более п итераций. Конечное число шагов — большое достижение для практики. Это обеспечивается поворотом главных осей линий уровня таким образом, чтобы одна из главных осей прошла через точку экстремума.
- 4. Для функции общего вида (а не квадратичной) метод сопряженных градиентов еще не разработан. Основная трудность в том, что матрица Гессе получается функциональной, т. е. зависящей от переменных.
Пример. Найти методом сопряженных градиентов минимум функции.
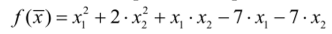
при начальных приближениях х° = (0,0); е = 5 • 10 2.
Так как функция f{x) — квадратичная, следовательно, оптимальное решение х*ор, должно быть найдено за 2 шага.
Вычислим градиент:
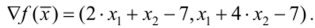
Шаг 1. По формулам (3.15) и (3.14) находим направление спуска и формируем функцию для нахождения длины шага.
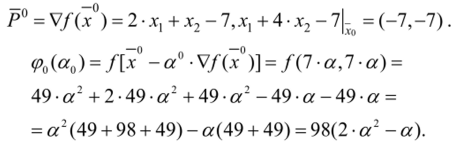
Из уравнения 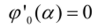 находим значение а:
находим значение а: 
По формуле (3.13) найдем новое значение вектора решений 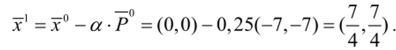
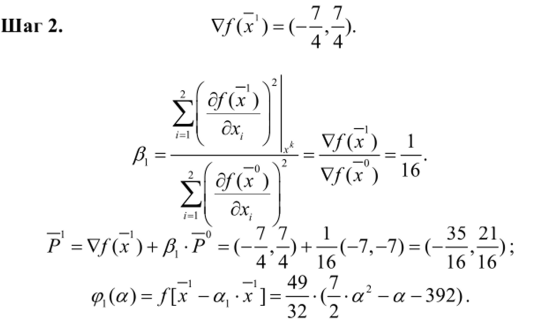
Следовательно,.

Проверим условия сходимости итерационного процесса (3.9):
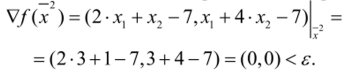
На рис. 3.17 приведены стратегии поиска для метода Коши и сопряженных градиентов, а в табл. 3.4 и 3.5 — численные результаты поиска.
Таблица 3.4.
Метод наискорейшего спуска (Коши)
Номер итерации. | V/(x*) = (х,*, х2*). | 5-С 1 II. уг Ус. | |
| 0,25. |
| |
| 0,503. |
| |
| 0,25. |
| |
| 0,497. |
| |
| 0,25. |
| |
| 0,503. |
| |
| 0,25. |
|
Метод сопряженных градиентов
Номер итерации. | V/(x*) = (x,‘-, x/). | -к Р | А. | ак | хк =(х, х2*). |
|
|
| |||
|
| 1/16. | 4/7. |
|
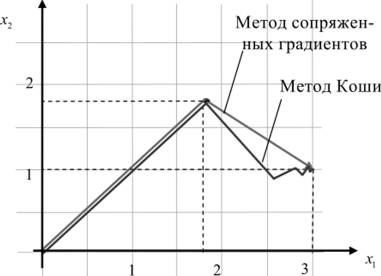
Рис. 3.17