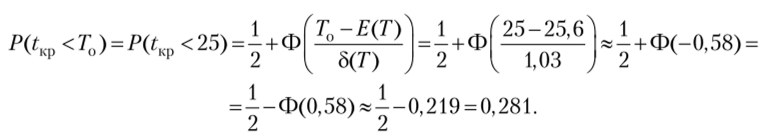Применение метода критического пути в построении сетевого графика

Как уже было сказано, критический путь — это самый продолжительный путь сетевого графика от начального до конечного события. Соответственно, все события и работы, находящиеся на этом пути, также называются критическими. Продолжительность критического пути определяет срок реализации проекта. На сетевом графике таких путей может быть несколько. У критических событий резерв времени равен нулю, так… Читать ещё >
Применение метода критического пути в построении сетевого графика (реферат, курсовая, диплом, контрольная)
Critical Part Method (СРМ), или метод критического пути, применяется с целью управления проектами в случае с фиксированным временем выполнения работ и позволяет ответить на следующие вопросы:
- 1) сколько времени необходимо для выполнения проекта в целом?
- 2) когда будут начинаться и заканчиваться отдельные работы проекта?
- 3) какие работы относят к критическим работам, которые должны выполняться в строго определенное графиком время?
- 4) на какое время можно отложить отдельные работы, не находящиеся на критическом ну ги сетевого графика?
Как уже было сказано, критический путь — это самый продолжительный путь сетевого графика от начального до конечного события. Соответственно, все события и работы, находящиеся на этом пути, также называются критическими. Продолжительность критического пути определяет срок реализации проекта. На сетевом графике таких путей может быть несколько.
Для определения параметров сетевого графика необходимо ввести следующие обозначения:
- — t (i; j) — работа и ее продолжительность с начальным событием г, конечным событием у;
- — ранний срок tp(j) наступления события у — это самый ранний момент времени, к которому завершаются все работы, предшествующие этому событию.
Правило вычисления:
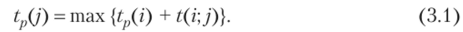
Максимум принимается по всем событиям /, непосредственно предшествующим событию у (соединены стрелками);
— поздний срок tn{i) наступления события i — предельный момент времени, после которого требуется столько времени, сколько необходимо для выполнения всех работ, следующих за этим событием.
Правило вычисления:
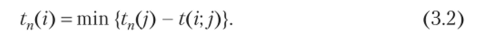
Минимум принимается по всем событиям у, непосредственно следующим за событием i.
Резерв события R (i) устанавливает предельно допустимый срок задержки события г без нарушения срока наступления завершающего события. Правило вычисления:

Критические события резервов не имеют.
Для удобства расчетов параметров сетевого графика разделим событие на четыре сектора (рис. 3.14). В левом секторе укажем раннее время наступления события, в правом — поздний срок наступления события, в верхнем секторе укажем порядковый номер события, в нижнем — резерв события.
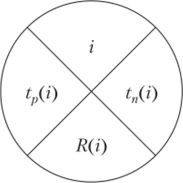
Рис. 3.14. Расчет параметров сетевого графика.
Резерв работы — предельно допустимый срок задержки работы без нарушения срока завершения проекта. Правило вычисления:
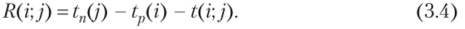
метод критического пути.
Пример 1. Имеются следующие данные.
Работа. | Непосредственный предшественник. | Продолжительность работы, нед. |
А | ; | |
В | ; | |
С | В | |
D | А | |
Е | А | |
F | D | |
Н | Е |
Необходимо определить критический путь инновационного проекта, рассчитать время завершения проекта, а также ответить на вопросы:
- 1) на какое время можно отложить работу D без отсрочки завершения проекта в целом?
- 2) можно ли отложить выполнение работы С без отсрочки завершения проекта в целом?
Строим сетевой график (рис. 3.15).

Рис. 3.15. Сетевой график № 1.
По правилам построения сетевого графика фиктивные работы (6; 9), (7; 9) и (8; 9) введены для того, чтобы было одно завершающее событие.
Расчеты.
1. При вычислении tp(i) перемещаемся, но сетевому графику от исходного события 1 к завершающему событию 9:
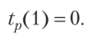
В событие 2 входит только одна работа: 
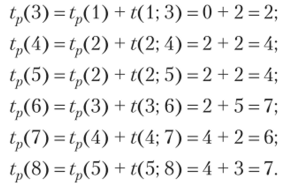
В событие 9 входят три работы:

2. При вычислении tn{i) перемещаемся от завершающего события 9 к исходному 1 по сетевому графику против стрелок:

Далее рассматриваем непосредственно предшествующее событие 8, из которого выходит только одна работа (8; 9):
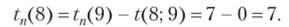
Аналогично:
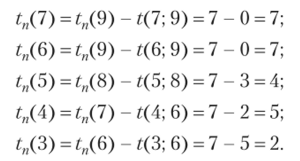
Из события 2 выходят две работы: (2; 4) и (2; 5). Поэтому определяем t"(2) по каждой из этих работ:

- 3. Вычисляем по R (i)=tn(i) — tp{i) резерв времени события г, т. е. из чисел, полученных на втором этапе, вычитаем числа, полученные на нервом.
- 4. У критических событий резерв времени равен нулю, так как ранние и поздние сроки их свершения совпадают. Критические события 1, 2, 5, 8, 9 определяют критический путь 1—2—5—8—9, а критические события 1, 3, 6, 9 определяют критический путь 1—3—6—9, которые на сетевом графике обозначаются жирной линией, в том числе штрихпунктирной (рис. 3.16).
Для завершения проекта потребуется 7 недель. Работа D = (2; 4) не расположена на критическом пути, ее можно задержать на tn(4) — tp{2) —1(2; 4) = = 5 — 2 — 2 = 1 (неделя). Работа С расположена на критическом пути, поэтому ее нельзя отложить без отсрочки завершения проекта в целом.
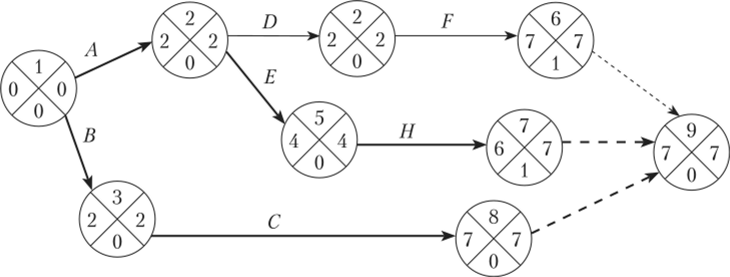
Рис. 3.16. Сетевой график № 2. Управление проектом с фиксированным временем выполнения работ Метод критического пути предполагал, что время выполнения всех работ в сетевом графике поддается точному измерению. В действительности это существенное огрубление проекта. На практике сроки реализации инновационного проекта заданы вероятностными величинами, т. е. необходимо применять для моделирования проекта сетевую модель с вероятностным временем выполнения работ. Сетевая модель с фиксированным временем выполнения работ может рассматриваться как исходная (базовая) простейшая модель для построения модели с вероятностным временем выполнения работ. Для управления проектом с вероятностным временем выполнения работ применяется модель PERT (от англ. Program Evaluation and Review Technique — «техника оценки и анализа программ (проектов)») с использованием вероятностных оценок времени выполнения работ в рамках инновационного проекта.
В этом случае для каждой работы устанавливают три временных характеристики, которые определяются экспертно на основе опыта специалистов и сотрудников проектно-ориентированной компании, не раз выполнявших подобного рода работы. В случае отсутствия таких экспертов можно обратиться к опыту сторонних специалистов или менторов.
В качестве временных характеристик принимают:
- — оптимистическое время а — минимальное возможное значение времени выполнения работы;
- — пессимистическое время h — максимальное возможное значение времени выполнения работы;
- — наиболее вероятное время т — наиболее вероятное время выполнения работы в нормальных условиях.
Минимальное время выполнения работы определяется исходя из предположения, что работа проходит без задержек, максимальное время — из расчета превалирования неблагоприятных условий ее выполнения. Наиболее вероятное время выполнения работ выбирается исходя из оценки эксперта, его опыта, т. е. оценка времени выполнения данной работы с учетом реального положения дел. Для важных, первостепенных проектов с целью определения временных параметров могут быть привлечены несколько экспертов, которые могут оценивать время выполнения работ по методике Дельфи.
По временным параметрам а, b и т находят ожидаемое время выполнения работы: 
а также находят отклонение ожидаемой продолжительности времени t (8 — дисперсию) по формуле:

Используя значение времени t, можно найти и построить критический путь сетевого графика.
Распределение времени Т завершения проекта является нормальным со средним Е (Т) и равно сумме возможных значений времени работ на критическом пути, и дисперсией 52(Г), равной сумме дисперсий работ критического пути при условии, если значения времени выполнения каждой из работ независимы друг от друга. В сетевом графике с вероятностным временем выполнения работ можно рассчитать такую задачу, как нахождение вероятности Р выполнения всего проекта к установленному сроку Т0.

Xх ( —t2 ^.
где Ф (.г) = .— Jexp —— dt — функция Лапласа. Значения функции нал/2тг О V ^ у ходятся по таблице Ф (-д:) = -Ф (х). Таблицы со значениями этой функции можно встретить практически в любом учебнике по теории вероятностей. При работе с программным пакетом Excel можно воспользоваться мастером функций fx 
Считают Ф (х) = 0,5 при х > 5.
Пример 2. Инновационный проект состоит из девяти основных работ1.
Работа. | Н епос родствен н ы й предшественник. | Оптимистическое время (а), дн. | Наиболее вероятное время (т)у дн. | Пессимистическое время (Ь), дн. |
А | ; | |||
В | ; |
1 Просветов Г. И. Управление инновациями: задачи и решения: учеб.-практич. пособие. М.: Альфа-Пресс, 2010. С. 127.
Работа. | Непосредственный предшественник. | Оптимистическое время (а), дн. | Наиболее вероятное время (т), дн. | Пессимистическое время (b), дн. |
С | А, В | |||
D | А, В | |||
Е | В | |||
F | С | |||
G | D | |||
Н | D, F | в. | ||
I | Е, G, Н |
Необходимо найти срок реализации проекта, стандартное отклонение времени его завершения, определить вероятность выполнения проекта при условии его продолжительности не более 25 рабочих дней. Ожидаемое время выполнения работы:
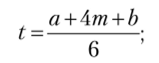
отклонение ожидаемой продолжительности времени t (дисперсия):
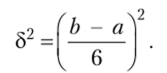
Работа. | а | т | Ь | а+4т+Ь t =; | l 6 J. |
А | 4,8. | 9/36. | |||
В | 16/36. | ||||
С | 4/36. | ||||
D | 8,8. | 9/36. | |||
Е | 16/36. | ||||
F | 4/36. | ||||
G | 7,8. | 25/36. | |||
Н | 16/36. | ||||
I | 4/36. |
Строим сетевой график (рис. 3.17) с указанием ожидаемой продолжительности каждой работы. Определяем критический путь и рассчитываем ожидаемый срок выполнения проекта.

Рис. 3.17. Сетевой график № 3.
Расчеты.
tp | 6,. | Критический путь. | Длина критического пути. |
tp ( 1) = 0. (р (2) = 4,8 tp( 3) = 4 *"(4) =10,8 tr(5) = 13,6 tp(6) = 13,6 tp ( 7) = 21,6 tp( 8) = 25,6. | 6,(8) = 25,6 6,(7) = 21,6 6,(6) = 13,6 6,(5) = 13,6 6,(4) =11,6 6,(3) = 4,8 6,(2) = 4,8 6,(1) = 0. | A-D-H-I | 25,6 дн. |
Дисперсия ожидаемого времени выполнения проекта равна сумме дисперсий критических работ:

Стандартное отклонение времени выполнения проекта составит:
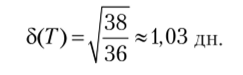
Найдем вероятность того, что выполнение проекта займет не более Т()=25 дней.