Сечения и фазовый объем

В предыдущей главе обсуждалось понятие поперечного сечения реакции и одна из популярных схем его измерения в экспериментах по рассеянию. Было упомянуто, что сечение некоторой реакции связано непосредственно с квадратом модуля амплитуды ее вероятности и размером области в т. н. «фазовом пространстве», в которой могут оказаться конечные продукты реакции. Обсудим здесь эту связь.

Сечения и матрица рассеяния

При вычислениях вероятностей переходов в единицу времени используется понятие матрицы рассеяния, или 5-матрицы, связывающей начальные (|г >) и конечные (|/ >) состояния частиц в рассматриваемом процессе. Она определяется так, что квадрат модуля ее матричного элемента определяет вероятность обнаружения определенного конечного состояния после того, как произошло взаимодействие. Ясно, что матричные элементы 5 -матрицы могут быть ненулевыми только тогда, когда полный 4-импульс конечного состояния V/ равен полному 4-импульсу начального состояния Vi, т. е. выполняется закон сохранения энергии-импульса. Это необходимое (но, очевидно, не достаточное) условие.

Понятие 5-матрицы рассматривалось еще в курсе квантовой механики, поэтому ограничимся здесь кратким напоминанием основпых моментов в получении связи между сечением (полным или дифференциальным) реакции и матричным элементом. Выделим (5-функцию сохранения 4-импульса в определении матричного элемента и перепишем его через «матрицу' перехода» Т:

где N нормировочный множитель, который является, фактически, произведением из нормировочных множителей волновых функций каждой из частиц, участвующих в реакции (г.е частиц и начального, и конечного состояний). Далее будем считать, что начальные частицы не имеют спина (это упростит запись формул), а начальные и конечные состояния не тождественны.

Вероятность перехода в единицу времени из состояния |г > в состояние |/ > связана с квадратом модуля матричного элемента:

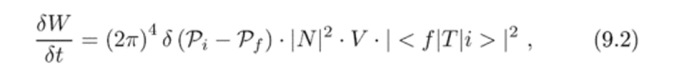
где V — нормировочный объем, а при получении выражения (9.2) было использовано соотношение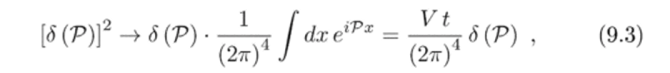

где одна дельта-функция была заменена интегралом по нормировочному объему и полному времени взаимодействия.

Вспоминая, как в предыдущей лекции определялось число столкновений нужного типа, видим, что для получения сечения рассматриваемой реакции надо разделить SW/St на поток падающих частиц и просуммировать по всем конечным состояниям рассматриваемого перехода, что даст.

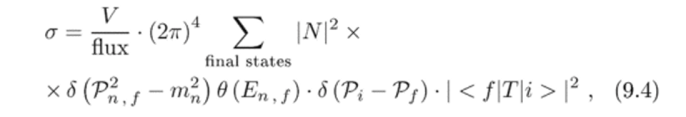
где V_nJ- 4-импульс n-й частицы конечного состояния |/ > (то есть, Vf = V_nj), и учтено также то обстоятельство, что все регистрируемые частицы находятся на массовой поверхности, т. е. V_{n ?} ,.

причем полная энергия n-й частицы положительна (поэтому в (9.4) появилась тета-функция).

Поток падающих частиц (например, взятый в системе покоя частицы-мишени), при нормировке волновых функций «на одну частицу в нормировочном объеме», равен просто отношению относительной скорости начальных частиц на величину нормировочного объема: flux = vq/V поэтому (9.4) принимает вид.

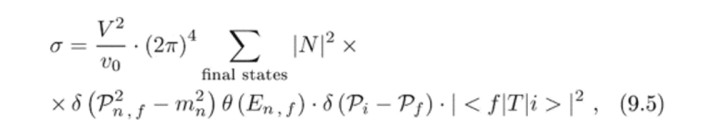
где относительная скорость t’o уже обсуждалась раньше и поэтому ее легко выписать:

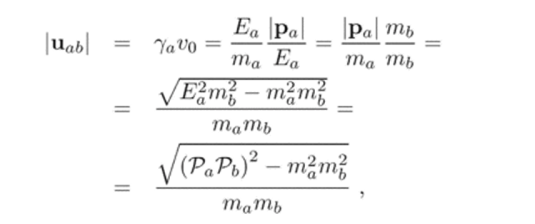
то есть, произведение (см. определение величины InvFlux в (8.3)).

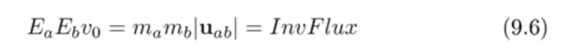
есть инвариант. Отсюда видно, что если выбрать нормировочный множитель для начальных частиц, а (и 6) в виде.

то (9.5) примет вид.

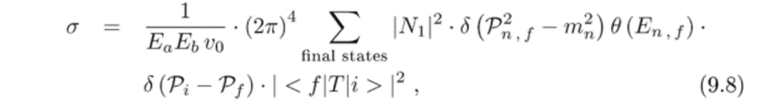
где N — содержит нормировочные множители только для частиц конечного состояния. Обсудим отдельные части этого выражения.^[1]

• • сумма, но всем спиновым состояниям (иногда — и другим состояниям, различающимся значениями дискретных квантовых чисел);
• • интегрирование, но 4-импульсам частиц конечного состояния.
• 2. При интегрировании по всем 4-импульсам имеется в вид}' инвариантный элемент объема d^AV_nj однако на самом деле, в силу того, что соответствующая частица находится на массовой поверхности (то есть, V*,/ ^{= т}п) ^и ее энергия положительна, интегрирование на деле идет по гиперповерхности, выделяемой дельта-функцией. Поэтому вместо четырех переменных в импульсном пространстве только три являются независимыми. В этом легко убедиться, выполнив интегрирование, но энергии (см. (9.15)).
• 3. Теперь становится понятным, почему в знаменателе нормировочного множителя в (9.7) появляется энергия.

С учетом сказанного, выражение (9.8) можно переписать как.

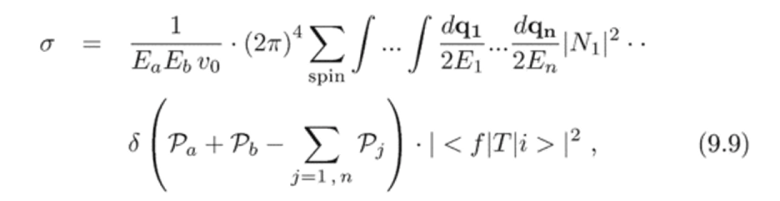
Из курса квантовой механики известно, что элемент объема сгр в импульсном пространстве включает {уК 2 ^7Г)³) d?p состояний, и, но ним тоже подразумевается суммирование. Поэтому.

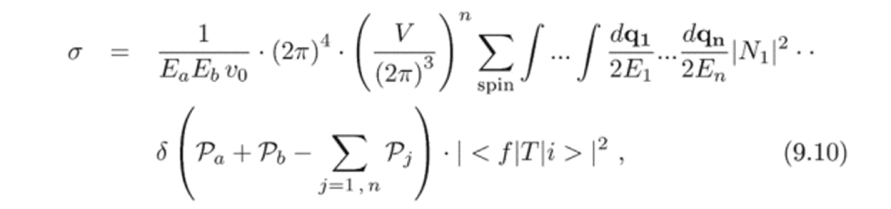
Фактически, нормировка одночастичных состояний уже выбрана (с точностью до множителей типа (27г)³) так, что нормировочный объем в (9.10) сокращается с соответствующим знаменателем, спрятанным в |Ni|². В итоге приходим к форме, где нормировочного объема, как и нормировочного множителя, уже нет:

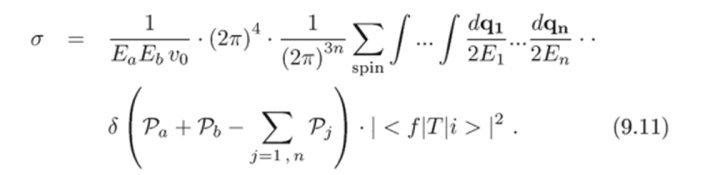
Возможны и другие соглашения о нормировках одночастичных состояний: от этого зависит лишь форма выражения, связывающего матричный элемент реакции с сечением, но не само численное значение сечения. Остается обсудить смысл формулы (9.11).

• [1] Под суммой, но конечным состояниям подразумевается: