Множество. 
Способы его задания. 
Характеристическое свойство множества

Есть в математике одно понятие, которое охватывает самый широкий, который только можно представить, класс объектов. Это понятие «множество». Оно обозначает совокупность объектов любой природы.

В жизни мы часто встречаемся со словами, которые обозначают множества конкретных объектов. Например, стая (птичья) — множество птиц.

Вместо слова «множество» можно использовать другие близкие, но смыслу слова. Так, можно сказать, что множество — это «совокупность»,.

«собрание», «семейство», «система», «класс» и т. д. Однако такие утверждения не являются строгими математическими определениями. При этом мы можем пояснить, что такое множество. Множество — это совокупность каких-либо предметов, объектов, явлений, которые рассматриваются как единое целое. Еще Георг Кантор^[1] говорил, что «множество есть многое мыслимое как единое». В этой фразе заключена главная характеристика любого множества.

Итак, понятие множества в математике является основным (неопределяемым) понятием. Представление о нем состоит в том, что это целостный объект, объединяющий в себе другие объекты любой природы.

Понятие «множество» в математике, как уже подчеркивалось, может обозначать разное число объектов. Их необязательно много. Нас не должно смущать слово, которое мы используем в русском языке для обозначения этого понятия. Например, в английском языке это понятие обозначают термином set, который переводится как совокупность. Например, множество имен, составляющих полное имя Георга Кантора, состоит из четырех элементов (Георг Фердинанд Людвиг Филипп), а множество естественных спутников планеты Земля состоит из одного элемента — Луна. Множества могут содержать как конечное число объектов, так и бесконечное. В первом случае множества называются конечными, во втором — бесконечными. Примерами бесконечных множеств могут служить множество звезд космического пространства, множество натуральных чисел, множество точек любой плоской или пространственной фигуры.

Есть множества, которые не содержат ни одного элемента, например множество квадратных кругов или множество саблезубых тигров, обитающих на Земле в наше время. Такие множества называются пустыми множествами.

Множества в математике обозначают заглавными буквами латинского алфавита: А, В, X,… Пустое множество обозначается особым знаком — 0. Для обозначения некоторых числовых множеств обычно используют определенные буквы (записанные специальным шрифтом): N — множество натуральных чисел; Z — множество целых чисел; Q — множество рациональных чисел; R — множество действительных чисел. Особым образом обозначаются части множества действительных чисел, которые называются числовыми промежутками. Есть открытые числовые промежутки, т. е. такие промежутки, указанные концы которых в них не входят. Их обычно обозначают с помощью круглых скобок. Например, запись (-1; 5) обозначает числовой промежуток, куда входят все действительные числа от -1 до 5, кроме самих указанных чисел. Есть закрытые числовые промежутки, в которые включаются их концы. Они обозначаются с помощью квадратных скобок. Например, [-1; 5]. Наконец, есть полуоткрытые/полузакрытые числовые промежутки: (-1; 5] или [-1; 5). Особо выделяются числовые промежутки, где одним из концов является плюс или минус бесконечность: (_оо; или [5_; +оо).

Графически множества изображают с помощью диаграмм Венна (их еще называют кругами Эйлера или диаграммами Эйлера — Венна)^[2]. Эта диаграмма схематически изображает множество в виде множества точек плоскости, ограниченных замкнутой кривой линией (окружностью). Точки этой замкнутой области (круга) изображают элементы множества (рис. 2.1).

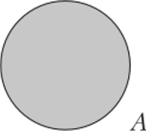
Рис. 2.1. Изображение множества на диаграмме Эйлера — Венна Числовые множества, прежде всего числовые промежутки, изображаются в виде отрезков на числовой прямой.

Например, на рис. 2.2 изображен промежуток (-2; 5].

Рис. 2.2. Изображение числовых промежутков Каждый объект, который входит в множество, называется его элементом. Элементы множества в математике принято обозначать прописными буквами латинского алфавита. При этом чтобы записать, что некий объект а является элементом множества Л, используют знак е (принадлежности), т. е. пишут а е А.

Читают эту запись по-разному: «а является элементом множества А» или «элемент а принадлежит множеству Л».

Для того чтобы записать, что объект b не является элементом множества А, используют знак ?, т. е. пишут h? А.

Эту запись читают следующим образом: «Ь не является элементом множества А» или «элемент Ъ не принадлежит множеству Л».

Если множество состоит из конечного числа элементов (такие множества называются конечными), то это множество можно задать, перечислив все элементы, которые в него входят. Такой способ задания множества называется способом перечисления элементов множества.

Например, множество Л состоит из трех чисел — 1, 2 и 3. Эту фразу в математике записывают короче с помощью фигурных скобок, т. е. Л = = {1,2,3}.

Далеко не любое множество можно задать перечислением его элементов. Трудно так задать множество, в котором содержится 1 000 000 элементов. Все эти элементы трудно назвать и записать. Но просто невозможно таким образом задать множество, в котором бесконечно много элементов. В этом случае используют другой способ задания множества — заданием характеристического свойства элементов, т. е. такого свойства, которым обладает любой элемент множества, и ни один из элементов, не входящих в множество, им не обладает. Именно это характеристическое свойство позволяет воспринимать совокупность элементов как единое целое.

Например, каждый элемент приведенного выше множества А = {1, 2, 3} обладает следующим характеристическим свойством — он является натуральным числом, меньшим четырех^[3]. Это записывают так: А = {х, хе N | х< 4}.

Давайте расшифруем следующую запись: В = {х, х е К | х < 3}. Здесь записано, что В — множество действительных чисел, меньших или равных трем. Это означает, что здесь характеристическим свойством задано множество, которое является числовым промежутком: В = (-(c)о; 3].

Заметим, что иногда множество в качестве элемента может содержать другое множество. Например, в множестве К = {1, {2}, 3} три элемента, два из них числа — 1 и 3 и один элемент — множество, состоящее из одного числа {2}. Приведем другие примеры:

• 1) Z = {Z⁺, Z", 0} — множество целых чисел Z состоит из двух множеств — целых положительных (или натуральных) чисел Z⁺, целых отрицательных чисел Z" — и числа 0;
• 2) а АВС, если рассматривать его как множество точек замкнутой ломанной, состоящей из трех звеньев, есть множество {(АВ), (ВС), (С А), А, В, С}, в которое входят три множества точек — открытые отрезки (АВ), (ВС), (СА), а также три точки — А, В, С.

Пример 2.1

Приведем пример множеств А, В, С, таких что Л е В, Be С, но Л не является элементом множества С.

Решая эту задачу, можно рассуждать следующим образом. По условию известно, что множество А должно являться элементом множества В. При этом в множество В могут входить и другие элементы, не являющиеся множествами, например А = {1}, а В = {{1}, 2}. Аналогично построим множество С: С = {{{1}, 2}, 3}. В этом случае множество А не является элементом множества С. Это можно установить, выделив все элементы множества С и сравнив их с элементами множества Л.

• [1] Георг Фердинанд Людвиг Филипп Кантор (1845—1918) — немецкий математик, основоположник теории множеств. Родился 3 марта 1845 г. в Санкт-Петербурге (Российскаяимперия), умер б января 1918 г. в Галле, Саксония (Германская империя).
• [2] Джон Венн (1834—1923) — английский математик. Он использовал эти замкнутыефигуры для изображения множеств в своей книге «Символическая логика», изданной в Лондоне в 1881 г. Намного раньше Леонард Эйлер (1707—1783) для изображения множествиспользовал круги. Позднее такие изображения получили названия диаграмм ЭйлераВенна.
• [3] Напомним, что в классической математике (об этом вы узнали в школе) множество натуральных чисел — это множество положительных целых чисел. Оно не включаетчисла нуль. Однако в некоторых разделах математики (а также в некоторых зарубежныхучебниках, но математике) число нуль относят к натуральным числам. Если вы будете изучать эти курсы, то соответствующие уточнения там будут сделаны.