Декартовы и декартово замкнутые дедуктивные категории

Мы получаем декартову дедуктивную категорию, если добавляем к обычным категорным тождествам следующие дополнительные уравнения между доказательствами:

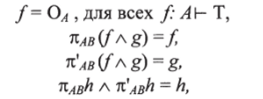
для всех /• Cl- A, g: ОВ, И: О- А л В.

Первое тождество очевидным образом утверждает, что Т есть терминальный объект. Эквивалентная формулировка имеет вид:

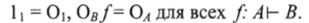
Второе из вышеприведенных тождеств утверждает, что, А а В есть произведение А и В с проекциями к_АВ и п'_АВ. Часто это записывается как А л В = А х В.

Следствием этого тождества является так называемый закон дистрибутивности:

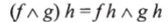
для всех/• Ch A, g: Cl- В, h: Dh С. Действительно, опуская нижние индексы, получаем:

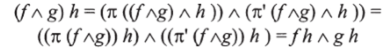
Часто также пишется.

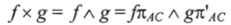
всякий раз, когда имеются стрелки f: А I- В и g: Cl- D, а кроме того заметим, что х: ДхЛ-«Л представляет собой функтор. Действительно, мы имеем: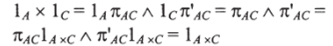

и, опуская нижние индексы, по закону дистрибутивности получаем:

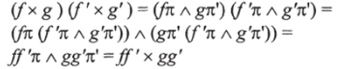
Декартово замкнутая дедуктивная категория представляет собой декартову дедуктивную категорию с дополнительной структурой, удовлетворяющей следующим тождествам:

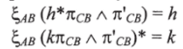
для всех h: С л ВА и к: О- В дз А.

Таким образом, декартово замкнутая дедуктивная категория представляет собой позитивное интуиционистское пропозициональное дедуктивное исчисление, стрелки которого выполняют вышеприведенные тождества.

Так же как мы записывали А л В = А х В, мы можем записывать А з В = ^(заимствуя общепринятую символику теории категорий). Стрелка q_An'- В⁴ х В h А обладает следующим универсальным свойством, называемым жепоненцированием:

для любой стрелки h:CxBА существует единственная стрелка h*: Cl- В^А, такая, что ^_в(й*хl_g) = h.

Большей частью именно в таком виде это свойство и фигурирует в литературе по теории категорий. Естественно, в нотации категорией логики все это можно переписать как:

для любой стрелки И.СлВI- А существует единственная стрелка Л*: Cl- A z> В, такая, что (/г* л _в) = h.

Для некоторого 1рафа X мы можем сконструировать позитивное интуиционистское исчисление D (X) и декартово замкнутую дедуктивную категорию Fr (X), свободно порожденную X.

С содержательной точки зрения Fr{X) будет представлять собой наименьшее позитивное интуиционистское исчисление, чьи формулы включают вершины X и чьи доказательства включают стрелки X. Логики обычно говорят о них как о «постулатах», хотя можег существовать несколько способов постулирования Xh Y, точно так же, как может существовать несколько стрелок ХY в X. Более формально формулы и доказательства определяются индуктивно следующим образом:

• • все вершины X являются формулами,
• • Т есть формула;
• • если А кВ суть формулы, то формулами будут А л В (= А х В) и А г> В (= В^А)
• • стрелки X и стрелки 1_А, 0_А, Для, я’яя и являются доказательствами для всех формул А и В,
• • доказательства замкнуты относительно правил вывода — композиции, конъюнкции выводов и правила дедукции.

Мы конструируем дедуктивную категорию FtX), свободно порожденную X, из D (X) путем наложения ограничений в виде тождеств между доказательствами, которые справедливы для декартово замкнутых дедуктивных категорий. Иначе говоря, мы получаем наименьшее отношение эквивалентности между доказательствами, выполняющее подстановочные законы и соответствующие тождества декартово замкнутой дедуктивной категории. Классами эквивалентности между доказательствами будут при этом стрелки F (X), но обычно в записи не различают доказательства и их классы эквивалентности.

Пусть Cart будет категорией декартово замкнутых дедуктивных категорий, чьими объектами являются декартово замкнутые дедуктивные категории, а стрелками — функторы F: А —> В, сохраняющие декартово замкнутую структуру на вершинах, т. е.

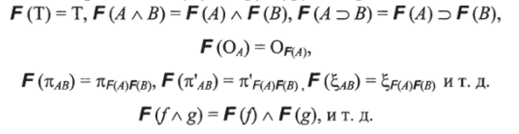
Пусть U будет обычным стирающим функтором Cart-^Grph. С каждым графом X мы можем ассоциировать морфизм графов Н*' X —г UF (X) следующим образом: Нх (Х)= X и, если / X —> Y есть стрелка в X, то Hx (f) = /(классы эквивалентности /рассматриваются как доказательства в D (X)). Имеет место следующее универсальное свойство:

Предложение 1. Для любой декартово замкнутой дедуктивной категории, А и любого морфизма графов F: X —" U (A) существует единственная стрелка F'. F (X) —" А в Cart, такая, что U (F')Hx= F.

Доказательство. Конструкция Р требует от нас выполнения следующих условий: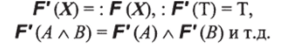

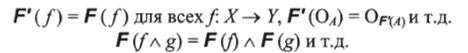
Требуется проверить, что функтор Р определен правильно, т. е. что для всех fg: Ah В в F' (X)/= g влечет Р if ) = Fg). Последнее очевидно, поскольку никаких других, кроме требуемых нам, тождеств в Р (X) не выполняется. ?

В декартовых или декартово замкнутых дедуктивных категориях тождество доказательств =_х должно быть таким, чтобы А[х] становилось декартовой или декартово замкнутой категорией, и чтобы функтор А -> А[х] сохранял декартову (декартово замкнутую) структуру. То есть, отношение эквивалентности = между доказательствами, рассмотренное для случая экспоненциальных категорий, должно также выполнять следующие условия:

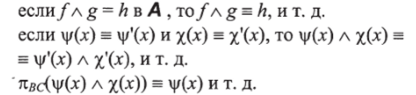
для всех у (х), |/'(*): Dh В и у (х), y'(x): Dh ВС.

Под декартовым (декартово замкнутым) функтором будем понимать функтор, сохраняющий декартову (декартово замкнутую) структуру на категориях. Пусть НхА -" Д[х] будет (декартовым, декартово замкнутым) функтором, отображающим f. Bh С на «постоянный» полином с тем же самым названием. В этом случае можно говорить о процессе подстановки доказательства а вместо х и рассмотреть функтор «подстановки» .

Предложение 2. Для данной (декартовой, декартово замкнутой) дедуктивной категории А, индетерминанта х: A oh, А над, А и стрелки a: A₀hA, существует единственный функтор S/: А[х]—>А такой, что S/(x) = а и S"^aHx= 1 д.

Доказательство. Вначале докажем, что:

Для данной дедуктивной категории А и индетерминанта х: A₀hA над А, функтора F: А-+В и любой стрелки b: F (A₀)h F (A) в В имеется единственный функтор FА[х] —> В, такой, что F (x)= Ь и F 'Н_х= F.

Каждое доказательство ср (х) при допущении х может иметь следующую форму: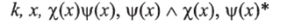

где к есть стрелка в А, т. е. постоянный полином. Решающим шагом является определение F '(ф (х)). Определим индуктивно:

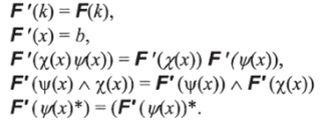
Остается лишь показать, что Р определен на полиномах, а не на доказательствах, то есть, что ф (х) =_х <�р'(*) влечет F '(ф.(х)) = = F.

'(ф'(х)). Если в последнем случае писать <�р (х) = ф'(х), то достаточно проверить, что = имеет все свойства подстановки и отвечает всем тождествам экспоненциальной категории. Например, чтобы проверить, что тс_СпХ (^х) л я’срОСОО = Х (^х)) мы вычисляем Р (ЛслХ (^х) ^Л n’cD%(x)) = n_FXC}FxD, F'(x (^x)) a n'_FXQFXD)F'(x (^x)) = ^F >(*) и т. д.

Теперь, чтобы получить доказательство нашего предложения, достаточно положить F = 1_Л ?

Обычно подстановка записывается в виде S/((p (x)) = <�р (я). Следующая теорема, называемая теоремой функциональной полноты, усиливает теорему дедукции для декартовых (декартово замкнутых) дедуктивных категорий:

Теорема 1 (функциональная полнота). Для любого полинома ф (х): ВС по индетерминанту х: ТЬ- А, над декартовой или декартово замкнутой дедуктивной категорией, А существует единственная стрелка f: А л ВС в А, такая, что/(хО_д л 1д) = <�р (х).

Доказательство. Пусть к_хеА <�р (х) будет определено как в доказательстве теоремы дедукции. Проверяем индукцией по длине доказательства <�р (х), что.

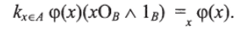
Действительно,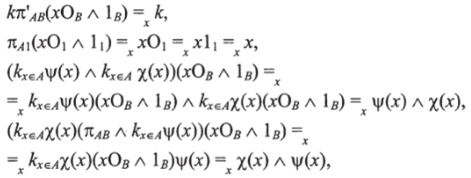

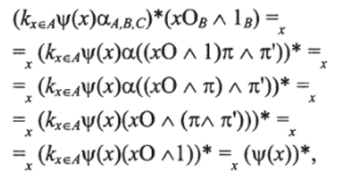
с помощью h*k = (h (k)(n_DBл п’ов))* и a((f a g) л /?) =/л (gA/?). Первое из этих равенств, справедливое для И: А л В -> С и k: D-+ А, легко получается при опускании нижних индексов: h*k= л.

71'))* = Й (й*я л я')(*я л я'))* = (Л (Ля л я'))*.

Следующим этапом является проверка того, что к_хеА ф (х) зависит от полинома ср (х), то есть, от класса эквивалентности доказательства ср (х) по модулю =_х. Будем писать ф (х) s ф (х) вместо к_хеА

ф (х) = к_хеА ф (х). Легко проверить, что s обладает всеми подстановочными свойствами и выполняет все условия, которые должно выполнять тождество в А[х]. Поскольку = было определено как наименьшее такое отношение эквивалентности, отсюда следует, что =_х содержится в =, т. е. что имеет место.

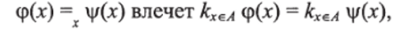
как и утверждалось.

Проверим, например, что если fAg = hbA, то fAg = h. Действительно:

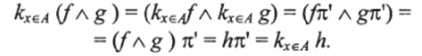
Наконец, чтобы доказать единственность / А а В -> С, допустим что j[xOв л 1*) = ф (*). Тогда можно утверждать, что / = к_хеА<�р (х). Действительно:

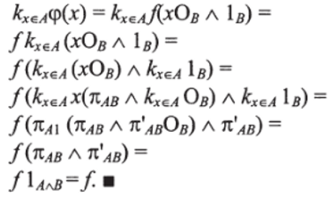
Следствие. Для любого полинома ф (х):ТН С по индетерминанту x: Tf- А, над декартовой или декартово замкнутой дедуктивной категорией, А существует единственная стрелка f: AС в.

A, такая, что g х = ф (х). Над декартово замкнутой дедуктивной

категорией, А существует единственная стрелка h: T-A z> С, такая, что л х) = (р (х).

Доказательство. Чтобы вывести это из предложения 8, достаточно положить.

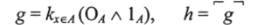
и проверить, что k_xsA (g х)(0_А л _А) = g и h^s — g. я

Именно это следствие чаще всего называют «функциональной полнотой» .