Нелинейные задачи диффузии в рамках модели двойной сорбции

Во многих средах диффузант способен адсорбироваться на неоднородностях среды, по которой осуществляется миграция. Адсорбция может происходить в соответствии с различными изотермами сорбции: Генри, Ленгмюра, Фрейндлиха, Дубинина-Астахова и др., причём в каждом компоненте структуры может реализоваться своя изотерма адсорбции, с присущими этому компоненту' параметрами изотермы (иногда и коэффициентами диффузии). В частном случае двухкомпонентной среды, находящейся в двух термодинамически различных состояниях типа 1 и 2, возникающие ситуации мог>т быть классифицированы по типам Г|-Г₂ (изотермы сорбции Генри для обеих компонентов среды, но с различными значениями констант растворимости), Л-Г (изотерма Генри для первого состояния и Ленгмюра для второго), ЛгЛ₂ (две изотермы Ленгмюра, каждая со своими параметрами), Г-Ф (изотермы Генри и Фрейндлиха), Д-Д (две изотермы Дубинина) и т. д. В рамках модели «двойной сорбции» возможны два диффузионных приближения: двухканальное, когда диффузия возможна по двум транспортным путям, и одноканальное, когда диффузия осуществляется только по одному типу местоположений. В рассматриваемых здесь моделях адсорбция происходит на нульмерных центрах, т. е. на центрах, не имеющих ни размера, ни формы.

Серьёзной проблемой является нелинейность практически всех задач диффузии при механизме двойной сорбции, что приводит принципиальной невозможности аналитического решения таких задач (также как диффузии при наличии химической реакции 2-го порядка, которая попутно рассматривается в этой главе). Поэтому исходные дифференциальные уравнения в частных производных приходится решать численными методами, что существенно затрудняет обработку результатов диффузионных экспериментов. Для облегчения задачи определения из экспериментальных данных параметров диффузии приходится выделять асимптотические режимы и уже их применять для нахождения параметров модели.

Рассмотрим миграцию в среде, в которой молекулы диффузанта находятся в двух состояниях — подвижном (состояние l) и неподвижном (адсорбированном или в дефектах-ловушках) — состояние 2.

Начнём с описания иммобилизации диффузанта за счёт адсорбции, подчиняющейся изотерме Генри (линейная изотерма адсорбции).

Если реакция иммобилизации происходит намного быстрее диффузии, то существует локальное равновесие между подвижной и неподвижной видами диффузанта. В простейшем случае, концентрация иммобилизованного диффузанта прямо пропорциональна концентрации подвижного вида С (линейная изотерма сорбции):

а=КС.

Уравнение диффузии при наличии адсорбции имеет вид:

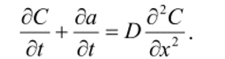
При наличии локального равновесия:

Постоянную К можно интерпретировать, как константу растворимости, как константу адсорбции по изотерме Генри или как константу равновесия обратимой химической реакции. Реакция замедляет диффузионный процесс. Так, если i+/C=ioo, то по сравнению с классической диффузией, миграция с адсорбцией будет замедлена в ЮО раз. Диффузия определяется эффективным коэффициентом диффузии D/(i+K).

В случае нелинейной изотермы адсорбции, а=КС^п, решения могут быть получены только численными методами.

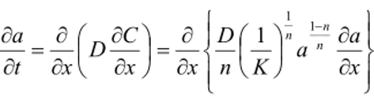
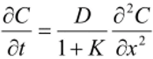
Если К велико, так что 8С/ 8t можно пренебречь по сравнению да/dt, то В этом случае процесс можно описывать как диффузию, в которой коэффициент диффузии зависит от общей концентрации диффузанта (в подвижной и неподвижной формах).

Если п<1 (изотерма адсорбции Фрейндлиха), то эффективный коэффициент диффузии возрастает с увеличением концентрации а:

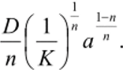
Если я>1, то коэффициент диффузии при росте концентрации уменьшается.