Статистическая проверка гипотез

Основные понятия статистической проверки гипотез

На разных этапах статистического исследования данных возникает необходимость проверки некоторых предположительных утверждений (гипотез) об изучаемых явлениях. Например, задачи на проверку гипотез могут формулироваться следующим образом.

• 1. Врач должен решить на основании выборочных данных обследования, является ли данное противогриппозное средство более эффективным по сравнению с другим, если время выздоровления неодинаково.
• 2. Врач должен решить на основании сравнения двух методик лечения одного и того же заболевания, что одна методика по эффективности превосходит другую или же выявленное различие случайно.
• 3. Производитель лекарств должен решить на основании выборки, выздоравливают ли 90% пациентов за время лечения, если они принимают новое противогриппозное средство.
• 4. Агроном должен решить на основании эксперимента, дает ли данное удобрение более высокий урожай по сравнению с другими и т. д.

Такого рода задачи могут быть решены путем выдвижения и проверки статистических гипотез. Статистической гипотезой называют любое предположение о виде или свойствах неизвестного распределения генеральной совокупности или о параметрах известных распределений.

Задачи статистической проверки гипотез в принципе решаются следующим образом. Относительно генеральной совокупности высказывается та или иная основная гипотеза (нулевая гипотеза) Но, которая подлежит проверке. Кроме нулевой выдвигается еще и конкурирующая (альтернативная) гипотеза Hi, которая будет признана верной, если будет отвергнута нулевая гипотеза Но- Простой называют гипотезу, содержащую только одно предположение, сложной — гипотезу, состоящую из конечного или бесконечного числа простых гипотез.

Пусть, например, генеральная совокупность имеет нормальное распределение и требуется проверить гипотезу о том, что ее математическое ожидание М{Х) равно некоторому гипотетическому числу ао. Нулевая и альтернативная гипотезы могут быть сформулированы следующим образом:

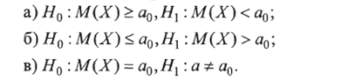
Обычно Но — гипотеза об отсутствии различий между сравнивающимися выборками (наблюдаемые различия случайны), Hi — гипотеза о наличии различий между сравнивающимися выборками (наблюдаемые различия достоверны и вызваны объективными причинами). Таким образом, в результате проверки будет пришл, а одна и только одна из гипотез, а вторая будет отвергнута.

Пример. 9.1. Декан факультета хочет проверить, повысится или понизится уровень успеваемости студентов, прослушавших курс по новой методике преподавания. Известно, что средняя успеваемость без нововведений составляет т = 4,1 балла. Сформулировать гипотезы.

Решение. Примем Яо — уровень знаний студентов не изменился, Hi — уровень знаний студентов изменился. Гипотезы в этом случае будут сформулированы следующим образом:

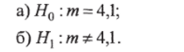
Пример. 9.2. Больной хочет снизить денежные расходы на лекарственные препараты, которые в среднем составляют с = 3000 р. в неделю. После принятия определенных мер по экономии расходных материалов больной хотел бы проверить, снизились ли расходы или остались на прежнем уровне.

Решение. Примем Яо — денежные расходы увеличились или остались на прежнем уровне, Н — расходы снизились. Гипотезы будут записаны так: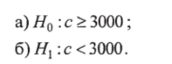

Статистическая проверка гипотез, основанная на выборочных данных, неизбежно связана с риском (вероятностью) принять ложное решение. При этом возможны ошибки двух родов. Ошибка первого рода произойдет, если будет принято решение отклонить верную нулевую гипотезу Но. Ошибка второго рода произойдет, если будет принято решение принимать нулевую гипотезу Но, когда она неверна. Вышесказанное можно представить в виде табл. 9.1.

Пример 9.3. Пациент пришел на прием к врачу. Сформулировать гипотезы и указать ошибки.

Решение. Обозначим гипотезы: гипотеза Н₀ — пациент здоров, H_t — пациент болен. Ошибка первого рода происходит, если здорового приняли за больного и начали лечить от несуществующей болезни, ошибка второго рода — если пациент болен, а его не лечат. Заметим, какая из ошибок является на практике более опасной, зависит от конкретной задачи. В данном случае ошибка первого рода чревата последствиями для здоровья пациента, а ошибка второго рода означает отказ от лечения больного и является более опасной.

Уровнем значимости (вероятностью ошибочной оценки) гипотезы называют вероятность совершить ошибку первого рода, т. е. отклонить нулевую гипотезу при условии, что она верна Ее вероятность принято обозначать буквой, а (равна уровню значимости гипотезы). Тогда доверительная вероятность исполнения выдвинутой гипотезы (нулевой гипотезы) будет равна у = 1 — а.

Обычно при проверке статистических гипотез принимают три уровня значимости а: 0,05, 0,01 и 0,001. Согласно требованиям фармакопеи в биологических исследованиях принимается, а = 0,05, а при разработке биологических стандартов, а =0,01. В биологических исследованиях часто считают достаточным уровень значимости, а = 0,05. При этом нулевую гипотезу Но принимают, если, а > 0,05 и отвергают, если а < 0,05. Если уровень значимости, а исследований лежит в пределах между 0,01 и 0,05, то необходимо осуществить дополнительные опыты, чтобы решить, следует ли отбрасывать нулевую гипотезу Но.

Уровень значимости выражается также в процентах. Если, например, принят уровень значимости, равный 0,05 (или 5%-й), то это означает, что в пяти случаях из ста рискуем допустить ошибку первого рода. При фиксированном объеме выборки можно сколь угодно уменьшать ошибку первого рода, уменьшая уровень значимости а. Иными словами, чем меньше а, тем менее вероятно допустить ошибку первого рода. Однако при этом возрастает вероятность ошибки второго рода. Поэтому единственным способом одновременного уменьшения ошибки первого и второго рода является увеличение объема выборки п.

Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что верна конкурирующая гипотеза. Если обозначить вероятность ошибки второго рода (принятия неправильной нулевой гипотезы) р, то мощность критерия равна 1~р. Следовательно, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода.

Таблица 9.1. К проверке нулевой гипотезы.

Для проверки принятой гипотезы, следовательно, и достоверности оценки генеральных параметров по выборочным данным используют величины, функции распределения которых известны. Ее обозначают t, если она распределена по закону Стьюдента, F — Фишера — Снедекора, G — Кочрена, С² — Бартлетта, х² — Пирсона «хи квадрат» и т. д. Функции распределения указанных величин сведены в специальные таблицы (см. таблицу прил. 3−10).

В дальнейшем с целью единообразия эту случайную величину с известной функцией распределения, по значениям которой принимают решение о принятии или отклонения выдвинутой нулевой гипотезы Но, будем именовать статистическим критерием А" . Сущность нулевой гипотезы Но сводится к предположению, что разница между генеральными параметрами сравниваемых совокупностей равна нулю, т. е. при нулевой гипотезе различия между наблюдаемыми выборочными характеристиками носят исключительно случайный характер. Значение статистического критерия, вычисленное по выборке, подчиняющейся определенному закону функции распределения случайной величины, принято называть наблюдаемым значением критерия А^ы;

После установления наблюдаемого значения критерия К_те" множество всех его значений разбивают на две области:

• а) область принятия гипотезы — множество тех значений критерия А, при которых гипотеза #о принимается;
• б) критическая область — множество тех значений критерия А, при которых гипотеза Но отклоняется или принимается альтернативная гипотеза Н.

Точки на числовой оси, отделяющие критическую область от области принятия гипотезы называются критическими точками Кщ, (их может быть одно или несколько). При этом различают левосторонние Якрл™ и правосторонние А_ч, ,_ф критические точки. Критическая точка Акр при известном распределении случайной величины X и заданном уровне значимости а находится по специальным таблицам критических точек распределения.

Положение критической области зависит от формулировки альтернативной гипотезы. Допустим, что для случайной величины X при заданной плотности вероятности Pwyfe) стандартного нормального распределения проверяется гипотеза Н₀: а=а₀. Возможны следующие варианты формулировки ачьтернативной гипотезы:

• а) Н а<�ао. В этом случае критическая область размещается в левом «хвосте» функции распределения Pn (o, i)(z) (рис. 9.1, а), задаваемая неравенством А<�Акр_ЛМ, где Акр"_е,<0 (рис. 9.1 б);
• б) Н. а>ао. Критическая область размещается в правом «хвосте» функции распределения Р_тi>(z) (рис. 9.2, а), задаваемая неравенством Я>А_кр «_р, где К_{кр пр}>0 (рис. 9.2, б);
• в) Критическая область размещается в обоих «хвостах» распределения Рьхo, ij (z) (рис. 9.3, а), задаваемая неравенством |А|>Ак_Р«_Р, где А_кр «_р>0 (рис. 9.3, б).

В первых двух вариантах критические области называются соответственно левосторонней и правосторонней. В третьем варианте критическая область двусторонняя и при этом различают две критические точки (А_ч, ,_та и Акрпр).

После построения критической области вычисляют значение критерия Анабл по выборке и сравнивают его с критической областью. Если значение критерия К_н, вп попадает в область принятия нулевой гипотезы Я₀, то гипотезу Я₀ принимают, а если в критическую область — то Но отвергают и принимают альтернативную гипотезу Н. Аналогично для двусторонней критической области при I^Hagnl^Kp нулевую гипотезу Я₀ отвергают, а если |Я"абл|<�Як_Р — нет оснований ее отклонять.

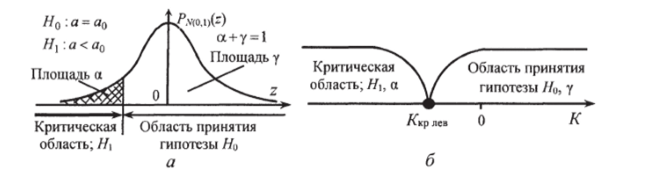
Рис. 9.1. Левостороння критическая область.

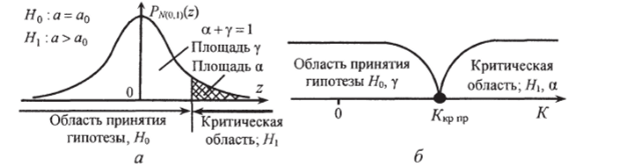
Рис. 9.2. Правостороння критическая область.

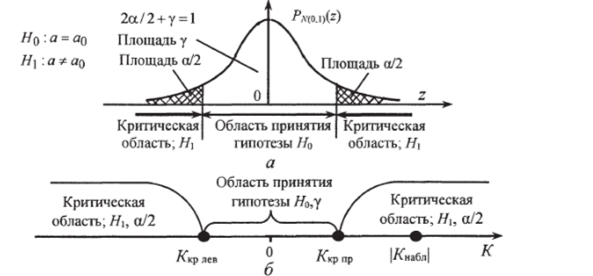
Рис. 9.3. Двусторонняя критическая область.

Пример 9.4. При /0^=1, Яиабл = 0,3 и уровне значимости, а = 0,05 построить двустороннюю критическую область, если критерий распределен по нормальному закону.

Решение. Критическая область двусторонняя (рис. 9.4), которая имеет две критические точки: К_кр «» = - I, _лр = 1.

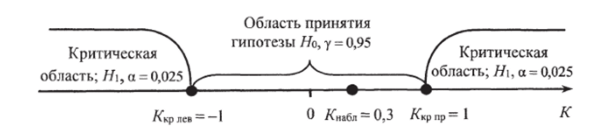
Рис. 9.4. Двусторонняя критическая область.