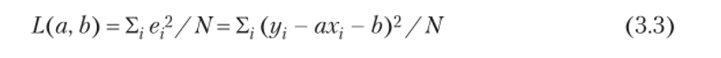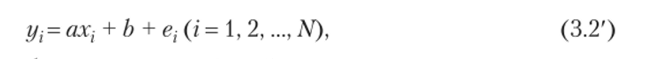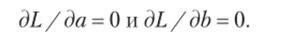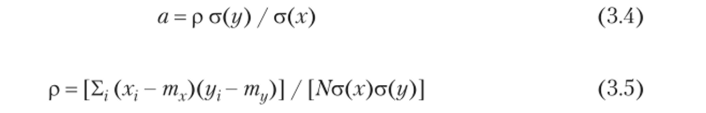Ф3. 2. Линейная регрессия: формулировки

ФЗ.2.1. Аппроксимация данных линейным уравнением

Определим параметры линейной регрессии. Имеется N объектов, для каждого из которых заданы целевой признак у и входной признак х: (х_{, у_{), (х₂, у2), г/д-). Вопрос в том, чтобы идентифицировать линейное уравнение, которое бы их связывало:

Точную подгонку коэффициентов можно произвести, только если все пары (.г, у!) лежат на одной и той же прямой в плоскости (х, у), что для реальных данных маловероятно. Это значит, что в уравнении (3.2) для каждой пары (x_if г/,) будет невязка, нс обязательно нулевая. В этом случае наше уравнение может быть записано в виде.

где е_г — невязки, или ошибки, регрессии. Явный учет 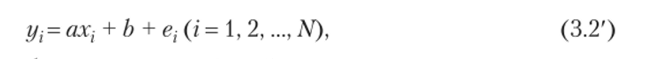невязок позволяет поставить задачу отыскания коэффициентов а и b так, чтобы остатки могли быть минимизированы, но критерию наименьших квадратов. Минимизируется средняя квадратичная ошибка.

по всем возможным а и b при заданных x_t и г/, (i = 1, 2, N). Эта задача мини

мизации легко может быть решена с использованием понятий математического анализа. В самом деле, L (a, b) — параболическая функция от а и 6, ветвями вверх, поэтому ее минимум находится в точке, где частные производные L (a, b) но а и b равны нулю (условие оптимальности первого порядка):

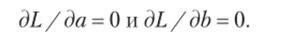
Предоставим математически ориентированному читателю найти выражения для этих частных производных, а также единственное их решение, в качестве упражнения. Решение можно выразить формулами (3.4)—(3.5) для а, и (3.6) — для b:

где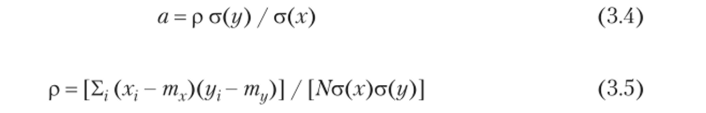

так называемый коэффициент корреляции, а т_х, m_lf — средние значения x_t и y_v соответственно;

Подставив оптимальные значения а и b в уравнении (3.3), можно получить выражение для минимального значения критерия (3.3):

Уравнение (3.2) называется линейной регрессией у пох, величина р в выражениях (3.4) и (3.5) — коэффициент корреляции, его квадрат р² в уравнении (3.7) — коэффициент детерминации и минимальное значение критерия L_m в уравнении (3.7) — нсобъяснснная часть дисперсии.