Алгоритм К-средних. 
Введение в анализ данных

• 0. Инициализация. Пользователь выбирает число К кластеров и назначает К гипотетических центров, см. рис. 4.11, а.
• 1. Обновление кластеров. При заданных К центрах c_k (k = 1, 2,…, К), каждый объект ге/ приписывается одному из центров по правилу минимального расстояния: вычисляются расстояния от i до каждого с_к, объект i приписывается ближайшему центру с_к, см. рис. 4.11, б. Те объекты, которые приписаны центру с_к, образуют кластер S_k (к = 1, 2,…, К), см. рис. 4.11, в. В качестве расстояния используется квадрат Евклидова расстояния.
• 2. Обновление центров. Вычисляется арифметический центр (центр масс) каждого кластера S_k, который и назначается новым центром с_к (к = 1, 2,…, К), см. рис. 4.11, г. Компоненты центра вычисляются как средние арифметические соответствующих компонент объектов из S_k.
• 3. Правило остановки. Новые центры с_к сравниваются со старыми. Если с_к ^{= с}к Д^ля каждого к = 1,2, …, К, то вычисления останавливаются и выдаются результаты: центр с_к и кластер S_k для каждого к= 1, 2,…, К. Если же хотя бы одно из равенств не верно, то каждый центр с_к заменяется вновь полученным центром с_к, и процесс возвращается к шагу 1. «Обновление кластеров».

Модель суммаризации, лежащая в основе метода, предполагает, что каждый кластер представлен своим центром, иногда также называемым стандартной точкой, или прототипом кластера [17, 18 j. Прототип как бы концентрирует в себе всю информацию о кластере.

Нормализованные данные компаний из табл. 1.2.

Таблица 4.8

Примечание. Шаги нормализации: (i) вычитание из столбцов их средних значений, (и) затем деление столбцов на их размахи и (iii) дополнительное деление трех последних столбцов, отвечающих трем категориям признака «Сектор экономики», на 1з. Последняя строка: вклады признаков в исходные данные, вычисленные как суммы квадратов элементов соответствующего столбца.

Рабочий пример 4.1. Кластеризация данных «Компании» методом К-средних

Рассмотрим нормализованные данные о компаниях из табл. 1.2 (табл. 4.9). Данные могут быть визуализированы в пространстве двух главных компонент (рис. 4.12) [17]. Возьмем для примера объекты «Ан», «Бр» и «Ви» в качестве центров трех кластеров. Теперь мы можем сравнить каждый объект с центром, чтобы понять, какой центр ближе к каждому конкретному объекту. Для сравнения любых двух точек использован квадрат Евклидовой меры вычисления расстояний (табл. 4.9). Каждый объект приписывается ближайшему центру согласно правилу минимального расстояния (табл. 4.10), в которой представлены все расстояния между объектами и центрами; жирным выделены те из расстояний, которые вычислены с помощью правила минимального расстояния.

Таблица 4.9

Вычисление Евклидовой меры между строками «Ав» и «Ан» в табл. 4.8 как суммы квадратов разностей между соответствующими ячейками.

Таблица 4.10

Расстояния между тремя компаниями — центрами и всеми остальными компаниями; каждый столбец матрицы показывает три расстояния между компанией и тремя центрами; наилучшие нары центр-компания выделены жирным.

Объекты, которые приписаны одному и тому же центру, формируют текущий кластер. Кластеры, найденные по табл. 4.10: S1 = {Ав, Ан, Ac}, S2 = {Бм, Бр, Бу}, и S3 = {Ви, By}. Приведенные кластеры соответствуют производимым продуктам. Метод К-средних подразумевает, что новые предполагаемые кластеры будут определяться теми же центрами.

Таблица 4.11

Предполагаемые кластеры и их центры, но табл. 4.10.

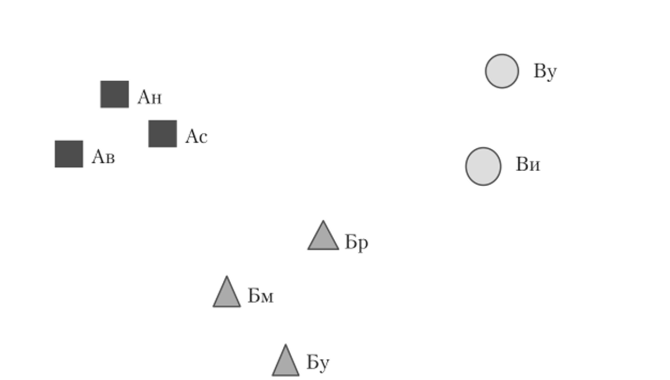
Рис. 4.12. Кластеры компаний, но нормализованным данным; они соответствуют выпускаемому продукту

Далее необходимо обновлять центры, используя информацию о текущих кластерах. Новые центры определены как их центры; компоненты центров — средние соответствующих компонент внутри кластеров, как показано в табл. 4.11.

Обновленные центры отличаются от центров предыдущего шага. Следовательно, повторяем итерацию метода К-средних. Для этого обновляются кластеры, используя расстояния между обновленными центрами и объектами (см. табл. 4.11). После этого получаем те же центры, так что объекты по правилу минимального расстояния будут приписаны тем же кластерам. Это означает, что процесс стабилизировался: новые итерации не могут ничего поменять. Процесс останавливается и возвращает найденные кластеры с центрами (в стандартизованной форме они представлены в табл. 4.11).

Таблица 4.12

Расстояния между тремя обновленными центрами и компаниями; наилучшие пары центр-компания выделены жирным.

Очевидно, что данный результат сильно зависит от способа стандартизации данных, сделанной перед началом вычислений, так как метод основан на расстояниях — суммах квадратов разностей значений различных признаков, которые сильно зависят от выбранных масштабов.

Самостоятельная работа

• 4.5.1. Проведите кластеризацию компаний, начиная с тех же объектов «Ан», «Бр» и «Ви» в качестве центров трех кластеров, при условии, что стандартизация данных выполнена путем вычитания средних арифметических с последующим делением на стандартные отклонения признаков.
• 4.5.2. Проведите кластеризацию компаний на два кластера, начиная с объектов «Ан» и «Ви» в качестве центров кластеров, не меняя стандартизацию признаков табл. 4.9.